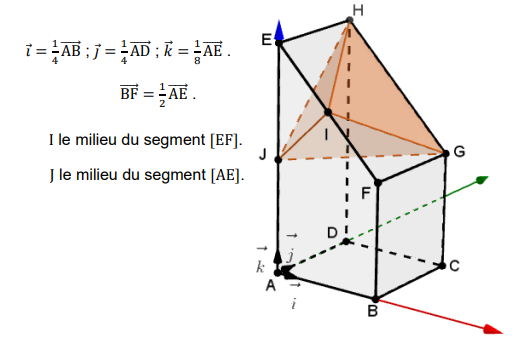
Géométrie, Mathématiques, bac général Centres étrangers 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... 1. Donner les coordonnées des points I et J. xI=(xE+xF) / 2 =(0+4) / 2 =2. yI=(yE+yF) / 2 =(0+0) / 2 =0. zI=(zE+zF) / 2 =(8+4) / 2 =6. I ( 2 ; 0 ; 6). xJ=(xE+xA) / 2 =(0+0) / 2 =0. yJ=(yE+yA) / 2 =(0+0) / 2 =0.   zJ=(zE+zA) / 2 =(8+0) / 2 =4.J ( 0 ; 0 ; 4).  2. Soit n le vecteur de coordonnées (−1; 1; 1 ). a. Montrer que le vecteur n est normal au plan (IGJ). 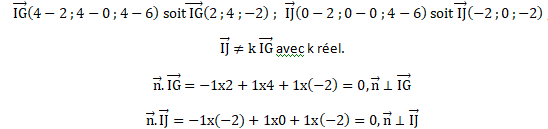 b. Déterminer une équation cartésienne du plan (IGJ). -x+y+z+d=0. I appartient à ce plan : -2+0+6+d=0 ; d =-4. -x+y+z-4=0. 3. Déterminer une représentation paramétrique de la droite d, perpendiculaire au plan (IGJ) et passant par H. Le vecteur n est un vecteur directeur de la droite d : x = -t+xH = -t. y = t +yH=t+4 ; z = t+zH =t+8 avec t  réel. 4. On note L le projeté orthogonal du point H sur le plan (IGJ). Montrer que les coordonnées de L sont ( 8/ 3 ; 4 /3 ; 16 /3 ). L appartient au plan : -xL+yL+zL-4=0. L appartient à la droite d : xL = -t ; yL =t+4 ; zL = t+8. t +t+4+t+8-4=0 ; t = -8 / 3. xL =8 / 3 ; yL =-8 / 3+4  =4 / 3; zL = - 8 /3+8= 16 / 3.  5. Calculer la distance du point H au plan (IGJ). HL = [(8 / 3-0)2 +(4 /3 -4)2 +(16 /3-8)2]½ =(64 / 9 +64 / 9 +64 / 9)½ =(64 / 3)½ =8 / 3½.  6. Montrer que le triangle IGJ est rectangle en I. IG2 =[(4-2)2 +(4-0)2+(4-6)2) =24 ; JG2 =[(4-0)2 +(4-0)2+(4-4)2) =32 ; IJ2 =[(0-2)2 +(0-0)2+(4-6)2) =8 ; JG2 =IG2 +JG2 ; d'après la réciproque du théorème de Pythagore, le triangle IGJ est rectangle en I 7. En déduire le volume du tétraèdre IGJH. Aire de la base IGJ : IJ x IG / 2 =2 x 2½ x2 x6½ / 2 =4 x3½. Hauteur  HL =8 / 3½. Volume  du tétraèdre = aire de base x hauteur / 3 = 4 x3½ x8 / 3½ / 3 =32 / 3. ... .... La figure ci-dessous correspond à la maquette d’un projet architectural. Il s’agit d’une maison de forme cubique (ABCDEFGH) accolée à un garage de forme cubique (BIJKLMNO) où L est le milieu du segment [BF] et K est le milieu du segment [BC]. Le garage est surmonté d’un toit de forme pyramidale (LMNOP) de base carrée LMNO et de sommet P positionné sur la façade de la maison. 1. a. Par lecture graphique, donner les coordonnées des points H, M et N. H(0 ; 2 ; 2 ) ; M(3 ; 0 ; 1 ) ; N (3 ; 1 ; 1). b. Déterminer une représentation paramétrique de la droite (HM). Coordonnées du vecteur HM : ( 3 ; -2 ; -1). Représentation paramétrique de la droite (HM) : x = 3t +xH  ; x = 3t. y =-2 t + yH ; y = -2t +2. z = -t+zH = -t +2 avec t réel.  2. L’architecte place le point P à l’intersection de la droite (HM) et du plan (BCF). Montrer que les coordonnées de P sont (2; 2 /3 ; 4 /3 ). Le vecteur de coordonnées (2 ; 0 ; 0) est orthogonal à ce plan : équation de ce plan : x+d=0. B(2 ; 0 ; 0) appartient à ce plan : xB+d=0 soit d = -2. Equation de ce plan x-2=0. P appartient à la droite (HM) : xP =3t ; yP = -2t+2 ; zP = -t+2. P appartient à ce plan : 3t-2 = 0 ; t = 2 /3. Par suite P(2 ; 2 /3 ; 4 /3).  . 3. a. Calculer le produit scalaire suivant :  b. Calculer la distance PM . PM= [12 +(-2/3)2 +(-1/3)2]½ =(1+4 /9 +1 /9)½ =14½ /3.  On admet que la distance PN est égale à 11½ /3.  c. Pour satisfaire à des contraintes techniques, le toit ne peut être construit que si l’angle MPN ne dépasse pas 55°. Le toit pourra-t-il être construit ? Le produit scalaire précédent s'écrit : 8 /9 = PM x PN x cos ( MPN) ; 8 /9 = 14½x 11½ /9  x cos ( MPN) ; 8 = 154½ cos (MPN) ; cos ( MPN) = 8 /154½~0,645. L'angle MPN mesure environ 50 °, le toit peut être construit. 4.  Justifier que les droites (HM) et (EN) sont sécantes. Quel est leur point d’intersection ? Droite HM : x = 3t ; y = -2t+2 ; z = -t+2. Coordonnées du vecteur EN : (3 ; 1 ; -1) Représentation paramétrique de la droite (EN) : x = 3k +xE = 3k. y = k+yE = k. z = -k+zE = -k+2 avec k réel. Hypothèse : les droites (HM) et (EN) sont sécantes. 3t = 3k ; -2t+2 =k soit k+2t = 2. -t+2 =-k+2 ; k=t. Par suite k = t =2 /3. Coordonnées du point d'intersection : (2 ; 2 /3 ; 4 /3). Ces deux droites se coupent en P.

menu