Autour
de Saturne,
bac général Asie
2023.
Lunette, diffraction, satellite
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| .. |
.
.
|
|
.
.
|
..
..
......
...
|
Observation de Titan à l'oeil nu.
Distance moyenne terre-Titan : D = 1,43 109 km.
Diamètre de Titan : d = 5,2 103 km.
1. Montrer que l'angle q sous lequel se présente Titan depuis la terre vaut environ 3,6 10-6 rad.
q = d / D = 5,2 103 / (1,43 109)=3,6 10-6 rad.
2. Justifier que Titan n'est pas observable à l'oeil nu.
q est inférieur au pouvoir séparateur de l'oeil ( 3 10-4 rad)..
3. En déduire le grossissement minimal que doit avoir l'instrument d'optique pour observer Titan depuis la terre..
Gmin = 3 10-4 / (3,6 10-6 )=83.
Observation de Titan à l'aide d'une lunette astronomique.
Objectif : f '1 =3,10 m ; diamètre d1 = 260 mm ;
Oculaire : trois distances focales sont possibles f '2 =12 mm ; 25 mm , 40 mm.
4. Sur le schéma identifier l'objectif et l'oculaire et positionner les foyers F2 et F'1 pour que la lunette soit afocale.
5. Construire la marche des rayons lumineux.
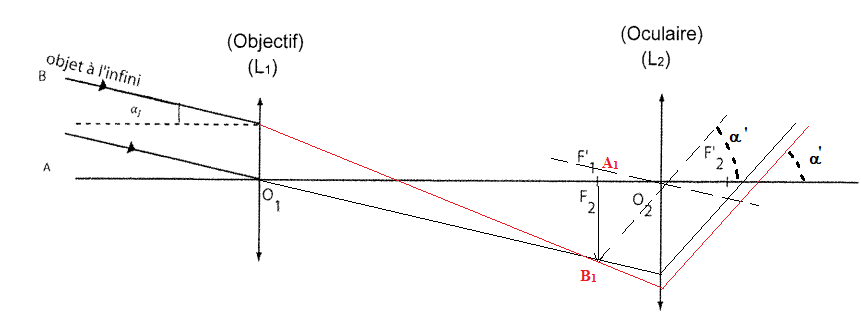
6 Etablir la relation G = f '2 / f '1.
Triangle O1A1B1 : tan a ~ a =A1B1
/ f '1.
Triangle O2A1B1
: tan a' ~ a' =A1B1
/ f '2
Par suite G = a'
/ a.=
f '1 / f '2.
7. Quel oculaire donne le grossissement maximal ?
G est maximal si f '2 est minimal : f '2 = 12 mm.
Gmax = 3,10 / 0,012 ~258.
8. Indiquer s'il est possible d'observer chacune des deux lunes, Titan et Janus, à l'aide de cette lunette.
Titan est observable : Gmax =258 > Gmin = 83.
Janus : angle sous lequel est vu Janus depuis la terre : 1,3 10-7 rad.
1,3 10-7 x Gmax = 1,3 10-7 x258 =3,4 10-5 rad.
Cette valeur étant inférieure au pouvoir séparateur de l'oeil, Janus n'est pas observable avec cette lunette.
9. Donner une estimation de la longueur L de cette lunette.
L = f '1 + f '2maxi = 3,10 + 40 10-3 ~ 3,14 m.
Limite d'observation de la lunette.
Le pouvoir de résolution d'un instrument d'optique est caractérisé par un angle a = 1,22 l / d.
l : longueur d'onde et d diamètre de l'objectif.
10. Nommer le phénomène qui limite le pouvoir de résolution.
La diffraction.
11. Pour l = 550 nm et G = 260, vérifier que la lunette permet d'observer Titan.
a = 1,22 x550 10-9 / 0,260 =2,58 10-6 rad.
Angle q sous lequel se présente Titan depuis la terre, observé à l'oeil nu : 3,6 10-6 rad.
Prendre en compte le grossissement de la lunette : 3,6 10-6 x260 ~9,4 10-4 rad.
9,4 10-4 > a, Titan est donc observable.
12. Expliquer pourquoi il est préférable d'utiliser des lunettes avec un objectif ayant un grand diamètre d'ouverture.
a = 1,22 l / d.
d intervient au dénominateur : si d est grand, a diminue : la limite d'observattion de la lunette augmente.
|
...
|
....
|
Autour de Saturne.
Les anneaux de Saturne sont constitués de morceaux de glace et de
poussière. Tout comme les lunes en orbite autour de Saturne, ils
obéissent aux lois du mouvement d'un satellite dans un champ de
gravitation.
Rayon de Saturne R = 58,2 103 km.
Rayon intérieur du premier anneau : rint = 6,69 104 km.
Rayon extérieur du premier anneau : rext = 7,45 104 km.
Rayon extérieur du dernier anneau : Rext = 1,36 105 km.
Rayon de l'orbite de Janus RJ = 1,51 105 km.
La vitesse v constante d'un satellite de masse m en orbite circulaire autour de Saturne est donnée par : v = (GM/r)½.
r est le rayon constant de l'orbite du satellite.
13. Retrouver cette relation.
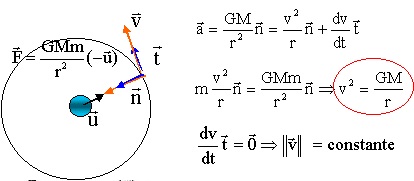
14. Retrouver la troisième loi de Kepler.
Le satellite décrit la circonférence 2 p r à la vitesse v en T seconde.
2pr = vT ; T = 2pr / v.
Elever au carré l'expression de la période : T2 = 4p2 r 2 / v2.
Remplacer v2 par son expression GM/ r : T2 = 4p2 r 3 / (GM).
15. Déterminer la masse de Saturne si la période de Janus est de 17 h.
T = 17 x3600=61 200 s.
Rayon de l'orbite de Janus RJ = r = 1,51 108 m.
M = 4p2r3 / (GT2)=4 x3,142 x(1,51 108)3 /(6,67 x10-11 x612002)=5,44 1026 kg.
16. Justifier que tous les corps du premier anneau ne tournent pas à la même vitesse.
Les corps du premier anneau ne sont pas tous à la même distance du centre de Saturne.
17. Déterminer le
nombre de tours effectués par la bordure interne du premier
anneau pendant que la bordure externe effectue un tour complet.
Text2 = 4p2 rext 3 / (GM).
Tint2 = 4p2 rint 3 / (GM).
Text2 / Tint2 = (rext / rint )3=(7,45 / 6,69)3=1,38.
Text / Tint =1,175.
La bordure interne effectue environ 1,2 tours.
|
|