Sujet 1.
Soit k un réel strictement positif.
Le but de cet exercice est de déterminer le nombre de solutions de l’équation
ln(x) = k x
de paramètre k.
1. Conjectures graphiques :
On a représenté, ci-dessous, dans un repère orthogonal, la courbe d’équation y = ln(x), la droite
d’équation y = x ainsi que la droite d’équation y = 0,2x :
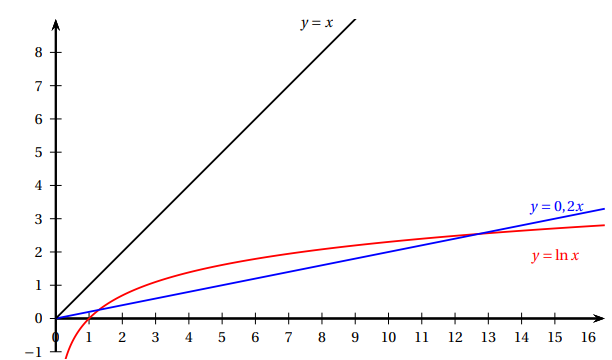
À partir du graphique ci-dessus, conjecturer le nombre de solutions de l’équation ln(x) = k x
pour k = 1 puis pour k = 0,2.
our k = 1, l'équation ln(x) = x n'a pas de solution.
Pour k = 0,2,
l'équation ln(x) = x a deux solutions.
2. Étude du cas k = 1 :
On considère la fonction f , définie et dérivable sur ]0 ; +∞[, par :
f (x) = ln(x)− x.
On note f
′
la fonction dérivée de la fonction f .
a. Calculer f
′
(x).
f '(x) = 1 /x-1 = (1-x) / x.
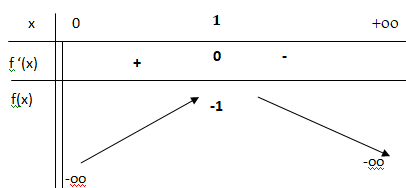
b. Étudier le sens de variation de la fonction f sur ]0 ; +∞[.
Dresser le tableau des variations de la fonction f en y faisant figurer la valeur exacte des
extremums s’il y en a.
Les limites aux bornes de l’intervalle de définition ne sont pas attendues.
 c.
c. En déduire le nombre de solutions de l’équation ln(x) = x.
x est striftement positif et f(x) strictement négatif ; l'équation ln(x) = x n'a pas de solution.
3. Étude du cas général :
k est un nombre réel strictement positif.
On considère la fonction g définie sur ]0 ; +∞[ par :
g(x) = ln(x)−k x.
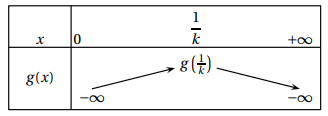
On admet que le tableau des variations de la fonction g est le suivant :
 a.
a. Donner, en fonction du signe de g (
1/
k )
le nombre de solutions de l’équation g(x) = 0.
Si
g (
1/
k ) < 0, l’équation g(x) = 0 n'a pas de solution.
Si g (
1/
k ) = 0, l’équation g(x) = 0 admet une seule solution 1 / k.
Si g
(
1/
k ) > 0 : f(x) est continue ( car dérivable) et
strictemennt croissante sur ]0 ; 1 /k] et 0 est une valeur comprise
entre -oo ( limite de g(x) en moins l'infini) et g(1/k) >0. D'après
le théorème de la bijection, l'équation g(x) =0 admet une solution
unique sur cet intervalle.
De même sur ]1/k ; +oo[, g est continue et strictement décroissante de g(1/k) à moins l'infini. D'après le théorème de la bijection, l'équation g(x) =0 admet une solution unique sur cet intervalle.
g(x) = 0 admet deux solutions dans ce cas.
b. Calculer g (1/k)
en fonction du réel k.
k >0, 1 / k >0 : 1 / k appartient à l'ensemble de définition de la fonction g.
g(1 / k) = ln(1 / k)-k *(1 / k) = ln(1 / k) -1 = -ln(k) -1.
c. Montrer que g (1/k)
> 0 équivaut à ln(k) < −1.
-ln(k) -1 > 0 ; -ln(k) > 1 ; ln(k) < -1.
d. Déterminer l’ensemble des valeurs de k pour lesquelles l’équation ln(x) = k x possède
exactement deux solutions.
D'après la question précédente, l'équation ln(x) = kx possède exactement 2 solutions correspond aux nombres k tels que :
ln(k) < -1 soit k < e
-1.
k appartient à ]0 ; e
-1[.
e. Donner, selon les valeurs de k, le nombre de solutions de l’équation ln(x) = k x.
Si k appartient à
]0 ; e-1[ l'équation admet deux solutions.
Si k = e-1, l'équation admet une solution.
Si k < e-1, l'équation n'a pas de solution.