Géométrie, Mathématiques, bac général Asie 2023.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Sujet 1.
Partie A.
 On considère deux cubes ABCDEFGH et BKLCFJMG positionnés comme sur la figure suivante :

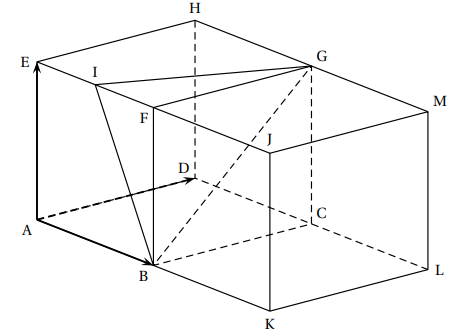
Le point I est le milieu de [EF]. Les points F, G et J ont pour coordonnées F(1; 0; 1), G(1; 1; 1) et J(2; 0; 1).
 1. Montrer que le volume du tétraèdre FIGB est égal à 1 /12 d’unité de volume.
Aire de la base, triangle rectangle FBG :  BF x FG / 2 = 1 x1 / 2 = 0,5.
Hauteur IF = 0,5.
Volume de ce tétraèdre : 0,5 x 0,5 / 3 = 1 /12 unité de volume.
2. Déterminer les coordonnées du point I.
I (0,5 ; 0 ; 1)
 3. Montrer que le vecteur DJ est un vecteur normal au plan (BIG).

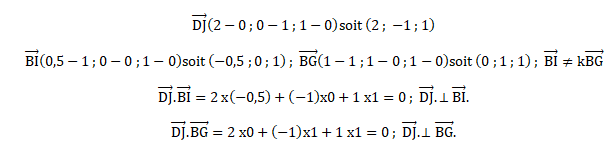 4. Montrer qu’une équation cartésienne du plan (BIG) est 2x − y + z −2 = 0.
2x -y+z+d=0.
B(1 ; 0 ; 0) appartient à ce plan : 2-0+0+d=0 ; d = - 2.
5. Déterminer une représentation paramétrique de la droite d, orthogonale à (BIG) et passant par F.
Coordonnées d'un vecteur directeur de cette droite : (2 ; -1 ; 1).
Représentation paramétrique de cette droite : x = 2t+xF = 2t+1.
y = -t+yF = -t.
z =t+zF = t+1 avec t réel.
 6. a. La droite d coupe le plan (BIG) au point L. Montrer que les coordonnées du point L sont ( 2 /3 ; 1/ 6 ; 5/ 6 ) .
L appartient au plan (BIG) : 2(2t+1)-(-t) +t+1 -2=0 ; 6t = -1 ; t = -1 / 6.
xL =2 x(-1/ 6) +1 = 2 / 3.
yL = 1 /6 ; zL =-1/6 +1 = 5 /6.
b. Calculer la longueur FL.
FL2 = (2 /3 -1)2 +(1/6-0)2 +(5/6-1)2=1 / 9 +1 /36 +1/36 = 6 /36 = 1 /6 ; FL = 1 /6½.
 c. Déduire des questions précédentes l’aire du triangle IGB.
Base BG:  [ (1-1 )2+(1-0 )2+(1-0 )2]½ =2½.
Hauteur FL : 1 /6½.
Aire de ce triangle : 2½ x1 /6½ / 2 =1 / 12½.

...
....

 Sujet 2.
On considère le cube ABCDEFGH.On considère les points M, N et P de coordonnées : M ( 1 ; 1 ; 3 / 4) , N( 0 ; 1/ 2 ; 1) , P( 1 ; 0 ; − 5/ 4 ) Dans cet exercice, on se propose de calculer le volume du tétraèdre FMNP.
1. Donner les coordonnées des vecteurs suivants.

2. Placer les points M, N et P sur la figure.

 3. Justifier que les points M, N et P ne sont pas alignés.
 Dès lors les trois points définissent le plan (MNP).
4. a. Calculer le produit scalaire suivant, puis en déduire la nature du triangle MNP.
 b. Calculer l’aire du triangle MNP.

Le triangle MNP est rectangle en M.
Aire de ce triangle : MP x MN / 2.
MN=[(-1)2 +(-0,5)2 +0,252]½ =(1+1/4 +1/16)½ =(21 / 16)½.
MP=[(0)2 +(-1)2 +(-2)2]½ =5½ .
Aire : (21 / 16)½ x5½  /2=(105 / 64)½=105½ /8.
 5. a. Montrer que le vecteur n de coordonnées (5 ; −8 ; 4) est un vecteur normal au plan (MNP).
 
b. En déduire qu’une équation cartésienne du plan (MNP) est 5x −8y +4z = 0.
5x -8y +4z +d=0.
N (0 ; 1/2 ; 1) appartient à ce plan :
-8 x1/2 +4x1+d=0 ; d = 0.
6. On rappelle que le point F a pour coordonnées F(1; 0; 1). Déterminer une représentation paramétrique de la droite d orthogonale au plan (MNP) et passant par le point F.
x = 5 t +xF = 5t+1.
y = -8t+yF = -8t.
z = 4t+zF =4t+1.
7. On note L le projeté orthogonal du point F sur le plan (MNP). Montrer que les coordonnées du point L sont : L(4 / 7 ; 24 /35 ; 23 /35)
L appartient au plan (MNP) : 5xL −8yL +4zL = 0.
Représentation paramétrique de la droite (FL) : x = 5 t +xF = 5t+1.
y = -8t +yF = -8t.
z = 4t +zF = 4t +1 avec t réel.
5 x(5t+1)-8(-8t) +4 x(4t+1)=0 ; 105t +9=0 ; t = -9 /105= -3 / 35.
xL = -15 / 35 +1 =-3/7+1=4/7.
yL =-8 x(-3/35)=24 / 35.
zL = 4 x(-3 /35)+1=23 /35.
8. Montrer que FL = 3 x 105 ½ / 35 puis calculer le volume du tétraèdre FMNP.
FL2 =(4 /7-1)2 +(24/35-0)2 +(23/35-1)2= (9 /49 +576 /352+144 /352=9 /49+720 / 352=9 x25 / (49 x25) +720 /(35x35)=945 / (35 x35)=27 /35.
FL2=9 x105 /352 ; FL = 3 x 105½ / 35.
Base du tétraèdre : triangle MNP d'aire 105½ / 8.
Hauteur relative à cette base : FL.
Volume = aire de base  x hauteur / 3 =105½ / 8 x105½ / 35 = 105 /(35 x8) =3 / 8.

  
menu