Mathématiques, Concours audiologie. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. Construction graphique. Soient la droite d1 d'équation y+2x-10=0 et la droite d2 parallèle à d1 passant par le point A de coordonnées (2 ; 2). Construire ces droites. Droite d1 : y = -2x+10. Elle passe par les points de coordonnées (0 ; 10) et ( 2 ; 6). La droite d2 étant parallèle à d1, son équation est y = -2x+b. A appartient à d2 : 2 = -2*2+b soit b = 6. 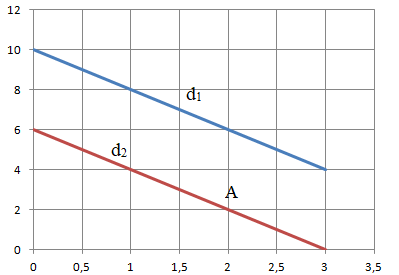Justifier comment obtenir l'ordonnée à l'origine de la droite d2. Intersection de cette droite avec l'axe vertical ( x = 0 ; y = 6) Dans un repère cartésien, on considère lles points A(2 ; 2), B(4 ; 1) ; C(5 ; -2). La droite d passe par les points A et B. La droite f perpendiculaire à d passe par C. Construiser ces droites. Equation de la droite d : y = ax+b. A appartient à cette droite : 2=2a+b. B appartient à cette droite : 1 =4a+b. Soustraire : 2-1 = 2a-4a soit a = -0,5. Par suite b = 3. y = -0,5x +3. Equation de la droite f, perpendiculaire à d ( le produit des coefficients directeurs est égal à -1) : y = 2x+b'. C appartient à f : -2 = 10+b' ; b' = -12. y = 2x-12. 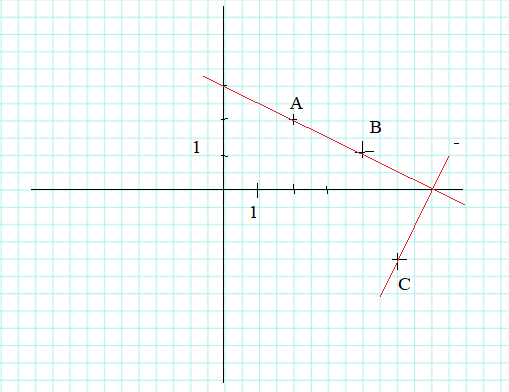Indiquer la somme des coordonnées du point d'intersection entre les droites d et f. Comment obtenir cette somme. Coordonnées du point d'intersection des droites ( 6 ; 0). 2x-12 = -0,5x+3. 2,5x = 15 ; x = 6. Par suite y = 0. Partie algèbre. Quelle expression est égale à racine carrée de x5 pour x positif ? x5 = x4 * x = (x2)2 *x. Racine carrée (x5) = racine carrée (x2)2 fois racine carrée (x) = x2 fois racine carrée (x). Soit le polynôme Q(x) = a2-9-a-3. Identifier l'ensemble des réels pour lesquels ce polynôme est positif. Q(x) = a2-a-12. Solution de a2-a-12 = 0. Discriminant D = (-1)2 +4*12 = 49 = 72. Solutions a1 = (1+7) / 2 = 4 et a2 = (1-7) / 2= -3. Le coefficient de a2 étant positif, Q(x) est strictement positif sur ]-oo ; -3[ union ]4 ; +oo[. Q(x) = (a+3) (a-4). 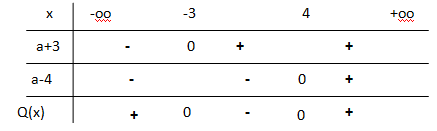Après avoir obtenu l'équation de la parabole ci-dessous, justifier les coordonnées du point P de la parabole d'abscisse 10. f(x) = ax2+bx+c. Le point de coordonnées(0 ; 0) appartient à la parabole, donc c = 0. Le point de coordonnées (4 ; 0) appartient à la parabole, donc 0 =16a+4b soit b = -4a. Le point de coordonnées (2 ; 2) appartient à la parabole, donc 2 =4a+2b soit 1 = 2a+b. 1 = 2a-4a = -2a ; a = -0,5. Par suite b = 2. f(x) = -0,5x2+2x. 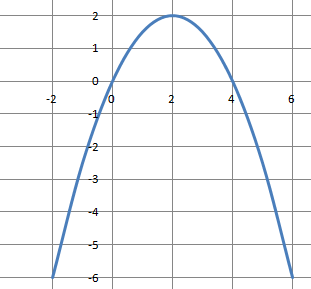Point P : x = 10 ; f(10) = -0,5 *102 +2*10= -30. Trigonométrie. On considère le nombre réel x tel que 0 < x < 2p et vérifiant : cox (x-0,5 p) = 1. cox (x-0,5 p) = 1 = cos (2kp). x-0,5 p = 2kp ; x = 0,5 p + 2kp  ; x = 0,5 p.  Que vaut sin (x+0,5 p) ? sin (x+0,5 p) = sin p = 0. Considérons le cosinus et le sinus d'un angle a dont l'amplitude  est comprise entre ]3p/4 ; p[. Pour un tel angle, quelle égalité est correcte ? 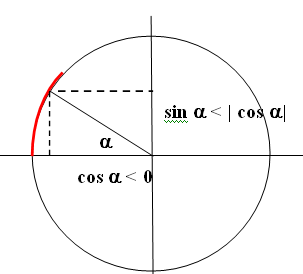Réponse A. Construire un triangle ABC tel que AB =  BC et où cos (B) = 3½ /2. En déduire l'angle C. L'angle B vaut 30 °. Le triangle est isocèle en B. Les angles  A  et C mesurent (180-30) / 2 = 75°. 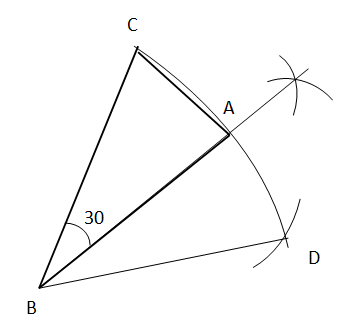Construire un triangle équilatéral BDC à l'aide du compas. Chercher le milieu de l'arc CD. ... .... Calcul de dérivée. Que vaut la dérivée de la fonction suivante en x = 1 ? Soit Q(x) une fonction quadratique dont la concavité est orientée vers le bas. Déterminer l'ensemble  des points pour lesquels l'expression Q(x) Q '(x) Q"(x) < 0. Que signifie Q(x) < 0 ; Q'(x) < 0 ; Q"(x) < 0 ? Q(x) =ax2+bx+c. Q'(x) = 2ax+b. Q"(x) = 2a. La dérivée seconde étant négative ( concavité tournée vers le bas) , a est négatif. Si Q'(x) < 0 ; alors Q(x) est décroissante. Si Q(x) < 0, on retient la partie de la parabole comprise entre ]-oo ; racine 1[ et ]racine 2 ; + oo[. Q"(x) étant négative, Q(x) Q '(x) doit être positif. C'est à dire Q(x) et Q'(x) doivent être du même signe. Q(x) > 0 et Q'(x) >0 soit Q(x) croissante. Q(x) < 0 et Q'(x) < 0 soit Q(x) décroissante. Obtenez les ensembles de nombres pour lesquels la fonction G(x) = 2 cos x vérifie G(x) G'(x) G"(x) >0 pour -10p < x <10p. G'(x) = -2 sin x . G"(x) = -2 cos x. G(x) G'(x) G"(x) =8 sin x cos2 x. sin x doit être positif ; x doit appartenir à ] 0+2kp ; p +2kp[ avec k entier appartenant à ]-4 ; 4[. Combien de fois la fonction G(x) est-elle entière lorsque 0 < x < 2p ? cos x = 0 ou cos x = 1. x = p / 2 ; x = 3 p/2 ;  x = p. Encadrement et simplification de racines. Encadrer au dixième près les nombres suivants : 2½ ~ 1,414 ; 2½ / 2 ~0,707. 0,7 < 2½ / 2 < 0,8. 3½ ~ 1,732 ; 3½ / 2 ~0,866. 0,8 < 3½ / 2 < 0,9. 3½ ~ 1,732 ; 3½ / 3 ~0,577. 0,5 < 3½ / 3 < 0,6. Réduire les expressions suivantes : Etablir la véracité des propositions suivantes en justifiant. Le nombre 1+3½ est la racine carrée du nombre 4+2*3½. Vrai. (1+3½)2 =1+3+2*3½= 4 +2*3½. Le nombre 1-3½ est la racine carrée du nombre 4-2*3½. Vrai. (1-3½)2 =1+3-2*3½= 4 -2*3½. Le nombre inverse de 1+3½ est le nombre 3½-1. Faux. 1 / (1+3½) = (1-3½) / [(1+3½)(1-3½)]=(1-3½) / (1-3) =(3½ -1) / 2. Le nombre inverse de 1+2½ est le nombre 2½-1. Vrai. 1 / (1+2½) = (1-2½) / [(1+2½)(1-2½)]=(1-2½) / (1-2) = 2½-1.

menu