Mathématiques, concours audioprothésiste 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Sujet 1.
Question 1. 10 points.
a. Définir et donner un exemple.
Un nombre irrationnel : le nombre de décimal est infini et non périodique.
Le nombre pi ; racine carrée (5).
Un domaine image d'une fonction : ensemble des valeurs possibles qui peuvent être obtenus en appliquant la fonction à un élément x. ]-oo ; +oo[ par exemple.
Une fonction paire : f(x) = f(-x) , le graphe est symétrique par rapport à l'axe des y ; exemple f(x) = x2.
Une symétrie axiale d'axe Ox : deux figures sont symétriques par rapport à une droite si elles sont supperposables par pliage le long de cette droite.
Un point d'inflexion : en ce point la courbe représentative d'une fonction change de convexité.
b. Dans le cercle trigonométrique, l'ordonnée du point d'intersection de l'angle x est sin (x)

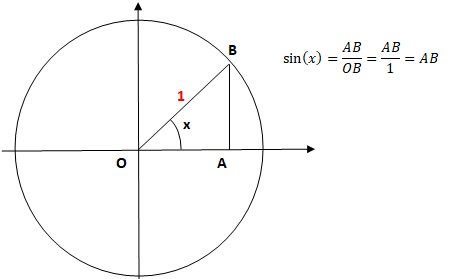c. Justifier l'encadremant suivant :
1,4 < racine carrée (2) < 1,5.
Racine carrée (2) = 1,414.
  2. Simplifier est exprimer le résultat  en notation scientifique.

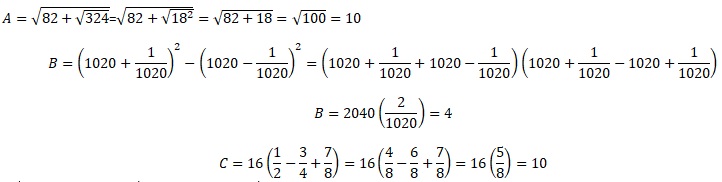
D =[3,2 x10-3 x5 x(102)3] / (4 10-2)=16 x 103 / (4 10-2) = 4 105.
E = log5(racine cubique de 5)= log5(51/3)=1 / 3 log5(5)= 1 /3 ln(5) / ln(5) = 1 /3.
log5(x) = ln(x) / ln(5).

  3. Trigonométrie (10 pts).
1. Montrer avec dessin à l'appui que tan(180 +x) = tan(x).

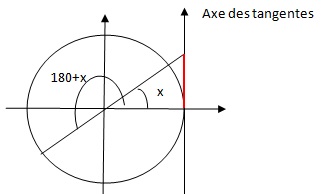2. Indiquer le signe des nombres trigonométriques suivants.
cos 250 < 0; 250° appartient au troisième quadrant.
sin 254 < 0 : 254° appartient au troisième quadrant.
cos (-325) = cos (325) >0 : 325° appartient au quatrième quadrant.
tan (-128) > 0 : 128 ° appartient au troisième quadrant.
cot 197 = 1 / tan 197 >0 : 197 ° appartient au troisième quadrant.
cot (298) = 1 / tan(298) < 0 : 298° appartient au quatrième quadrant.

 3. A partir des valeurs remarquables, calculer :
sin(3p/8)=sin( 4 p /8 -p/8)=sin (p/2-p/8)= cos (p/8).
cos(-120) = cos (120) = cos (90 +30) = -sin(30) = -0,5.
tan(315) = tan(180 +135)=tan(135) =tan(90 +45) =-tan(45) = -1.

4. 5 Représenter graphiquement y = 3 cos (2x-p/2).
Déterminer le tableau de variation et la concavité de la fonction.

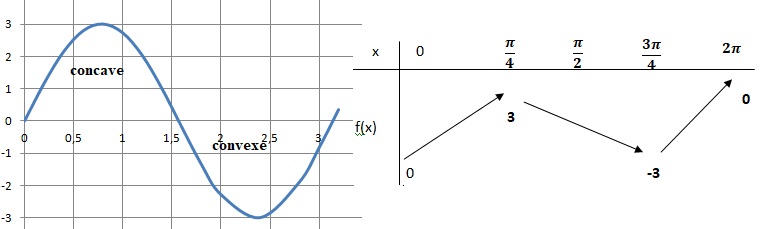  6. résoudre 0 < cos (x)  < 0,5.
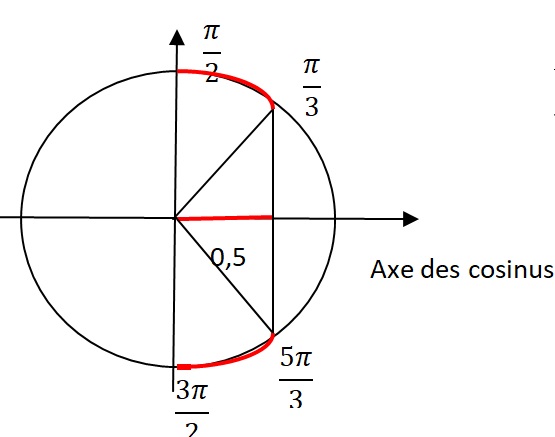
  Exercice 3 10 points.
1.a. Représenter graphiquement les fonctions suivantes.
f(x) = |2x+5| et g(x) = |5x2-20|
Si x < -2,5  f(x) = -(2x+5) sinon f(x) = 2x+5.
Si x  appartient à [-2 ; 2]; g(x) = -(5x2-20) sinon g(x) = 5x2-20.

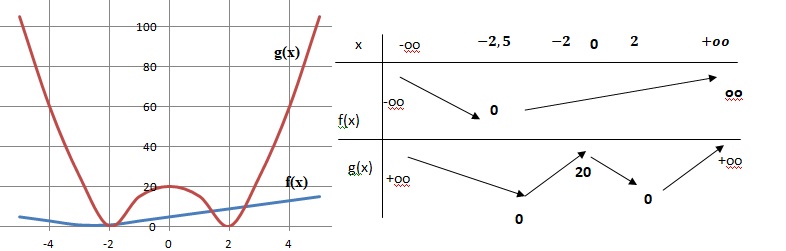
Déterminer l'antécédent de 5 par f .
5 =2x+5 ; x = 0.
5 = -2x-5 ; x = -5.
Déterminer l'image de 3 par g.
g(3) = | 5*32-20| =25.

   2. Résoudre : (5 points) .
a. Résoudre par deux méthodes différentes : 6x /(x2+9) = -1.
6x = -x2-9 ; x2+9+6x =0 ; (x+3)2 = 0 ; x = -3.
x2+9+6x =0 ; discriminant D =62-4 *9 = 0 ; x = -6 /(2) = -3.
b. résoudre graphiquement le système d'inéquations suivantes :
3x-y+4 < 0 et x+2y-2 > 0.
y >3x+4 et y >1-0,5x.

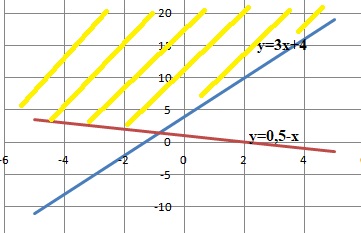3. (5 points)
a. Quel est le domaine de définition de la fonction suivante :
f(x) = (1-x2)½ / (x log(x)).
La racine carrée doit être positive ou nulle soit x appartenant à [-1 ; +1].
log (x) : x doit être strictement positif.
Le dénominateur ne doit pas être nul soit x différent de zéro et log(x) différent de zéro soit x différent de 1.
Domaine de définition : ]0 ; +1 [.
b. Préciser si les fonctions suivantes sont convexes ou non.
F(x) = log(-x3) et G(x) = (5)x. Justifier.
On dérive : F '(x) = -3x2 / (-x3 )= 3 /x ; F "(x) = 3 *(-1) / x2 = -3 / x2.
F "(x) < 0, la fonction f(x) est concave.
G(x) =5x = exp(x ln(5))
G '(x) = ln(5) .exp(x ln(5))
G "(x) =[ ln(5) ]2 exp(x ln(5)) >0, donc G(x) est convexe.

4. 5 points.
Calculer les dérivées des fonctions suivantes.
f(x) = x½ + 1/x½ =x½ + x-½ .
f '(x) = 0,5 x-½ -0,5 x-3/2.

g(x) = sin3(3x+4).
On pose u =3x+4 ; u' = 3
g '(x) = 3 cos(3x+4) sin2(3x+4).

h(x) = tan [ ( x2-x) / x] = tan(x-1).
h '(x) = 1 /cos2(x-1).

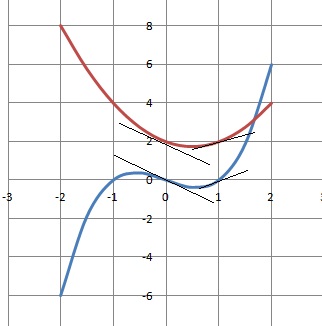
5. Après avoir représenter le graphe de chaque fonction, en quel point les graphes représentant les fonctions admettent-ils des tangentes parallèles ?
f(x) = x3-x ; g(x) = x2-x+2.
Calculer l'équation de ces tangentes et les représenter.
f '(x) = 3x2-1 ; g'(x) =2x-1.
Si les tangentes sont parallèles  : f '(x) = g'(x).
3x2-1 = 2x-1
3x2 = 2x ; 3x2-2x=0  ; x(3x-2).
x = 0 et x = 2/3.
Pour x = 0, équation des tangentes : y = f '(0) x +b = -x+b.
Le point de coordonnées (0 ; g(0) =2 appartient à l'une des tangentes ; y = -x+2.
Le point de coordonnées (0 ; f(0) =0 appartient à l'une des tangentes ; y = -x.
Pour x = 1/3, équation des tangentes : y = f '(2/3) x +b = 1/3x+b.
Le point de coordonnées (1/3 ; g(2/3) =2 appartient à l'une des tangentes ; y = 1/3x+16/9.
Le point de coordonnées (2/3 ; f(2/3) =-10 / 27 appartient à l'une des tangentes ; y = 1/3x-16/27.


6. Après avoir représenté la fonction, rechercher les racines et l'extremum de la fonction f(x) = 8 /(4+x2)-1.
Justifier qu'il n'y a pas de points d'inflexion.

...
....
Sujet 2.
a (10 points)
Définir et donner un exemple.
un nombre rationnel :
Ce nombre peut s'exprimer comme le quotient de deux entiers relatifs ; exemple -2 / 3.
un domainde de définition d'une fonction :
Un domaine image d'une fonction : ensemble des valeurs possibles qui peuvent être obtenus en appliquant la fonction à un élément x. ]-oo ; +oo[ par exemple.
Une fonction croissante.
Si x1 < x2, alors f(x1 ) < f(x2). Exemple f(x) = x ; g(x) = ln(x).

 Expliquer et justifier le domaine de définition de la fonction :
f(x) = (x-1) / [ |2x+1| -3|2-x| ]
Le dénominateur ne doit pas être nul.
|2x+1| -3|2-x| différent de zéro.
Si x > 2 : |2-x| = x-2 et |2x+1| = 2x+1.
2x+1-3(x-2) = -x+7 ; soit x différent de 7.
Si x < -0,5 : |2x+1|= -1-2x et |2-x| = 2-x.
-1-2x-3(2-x) =x-7 soit x différent de 7, toujours vérifié.
Si-0,5< x < 2 : |2x+1|=2x+1 et |2-x| =2-x.
2x+1+3(2-x )= -x+7 soit x différent de  7, vérifié..

b. Compléter :
sin a =a / c ; cos a = b / c ; tan a =a / b ; sin ß =b / c ; cos ß =a / c ; tan ß =b /a.

c. Justifier l'encadrement 1,7 < racine carrée (3) < 1,8.
racine carrée (3) = 1,732.

2. 10 points
a. Evaluer le polynôme P(x) =x2-4x+1 en x = 2 -3½.
p(x) =(2-3½)2 -4(2-3½)+1=4+3-4*3½-8+4*3½+1=0.
b. Simplifier :

3. Trigonométrie 10 points
1. Evaluer les angles en radian.
60 ° = p /3 ; -75° = -75 p / 180 = -5 p / 12 ; 270° = 270 p / 180= 3 p / 2 ; 1 tour = 2 p ; 0,5 tour = p ; 1 /3 tour = 2 p/3.
2. Soit le point P intersection de l'angle au sommet O avec le cercle trigonométrique. Si l'amplitude de l'angle est donnée en radian, quelles sont les coordonnées de P ?.
q= p ; P(-1 ; 0) : q= p /3 ; P(0,5 ; 3½ /2) ; q=5 p /3 ; P(0,5 ; -3½ /2) :
3. Evaluer : sin (p/2) = 1 ; cos ( 7 p /6) = - cos (p/6) = -3½ / 2 ; tan ( 5 p/4) = tan (  p/4) = 1.
4. Résoudre les équations suivantes dans le troisième quadrant uniquement. ( x appartient à [p ; 3p/2] soit [3,14 ; 4,71 rad] ou (-1,57 ; -3,14 rad]
sin(x-2) = 1 ; sin (x-2) = p / 2+2kp ; x-2 = p / 2+2kp ; x = 2 + p / 2+2kp ; k = 0.

2 sin ß -1 = 0 ; sin ß = 0,5 =sin p/6  ; ß =p/6+2kp et p-p/6 + 2kp.
Aucune solution dans le troisième quadrant.

sin ß = tan ß = sin ß / cos ß soit cos ß = 1 ; ß = ± p.

Sujet 3. 10 points.
1.a.Représenter graphiquement f(x) =|3-3x| et g(x) = |3x2-3|.
Si x >1  ; f(x) = 3x-3 sinon f(x) = 3-3x.
si x appartient à [-1 ; +1], g(x) = 3-3x2 sinon g(x) = 3x2-3.

b. Déterminer l'antécédent de 5 par f.
Si x >1  ; f(x) = 3x-3  = 5 soit x = 8 /3 sinon f(x) = 3-3x = 5 soit x = -2 /3.
c. Déterminer l'image de 3 par g.
g(3) = 3 *32-3 = 24.
d. Etudier la croissance de f et g sans dériver.

2.a. résoudre  12x / (x2+36) = -1.
12 x = -x2-36 ; x2+12x+36 =0.Discriminant D = 122-4 *36 = 0 ; x = -12 / 2 = -6.
ou  bien (x+6)2 = 0 soit x = -6.
b. Résoudre graphiquement le système suivant :
-1 < x < 3 et -2 < y < 4 et x+y-5 < 0 soit y < -x+5.


3. Simplifier l'expression suivante :

Quel est le domaine de définition de la fonction suivante ?
f(x) = x / (x-ln(x).
ln( x) est défini sur ]0  ; +oo[
Quel que soit x >0, x-ln(x) n'est pas nul.
Préciser si les fonctions suivantes sont convexes ou non.
F(x) = -log(x2) et G(x) = 5-x.
F '(x) = -2x / x2 = -2 /x ; F"(x) =2 /x2.
F"(x) est positive ; F(x) est convexe.
G(x) = exp(-x ln(5)) ; G'(x) = -ln(5) exp(-x ln(5)) ; G"(x) = ln(5)2 exp(-x ln(5)).
G"(x) est positive ; G(x) est convexe.

4. Calculer les dérivées premières des fonctions :
f(x) = -x½ +(1-x) / x½.
Dérivée du second terme :on pose u = 1-x et v =x½ ; u' = -1 ; v' = ½ x-½.
(u'v-v'u) / v2 = (-x½ -½(1-x)x-½) / x = -x½(1+0,5(1-x) / x = -(1,5 -x) / x½.
g '(x) = -0,5 x-½-(1,5 -x) / x½ = -0,5 x-½-(1,5 -x)  x-½ = x-½ (-2+x).

g(x) = cos3(3x+4).
Dérivée de cos (3x+4) : -3 sin(3x+4)
g'(x) = -3 sin(3x+4)cos2(3x+4).

h(x) = sin ((x2-x) / x) = sin(x-1) ; h '(x) = cos (x-1).

5. Représenter la fonction suivante, rechercher les racines et l'extremum. Justfier l'existence d'un point d'inflexion.
f(x) = 2x3-2x.
Racines : 2x(x2-1) =0 soit x = 0 ; x =±1.
Extremum :  f '(x) = 6x2-2 ;
f '(x) = 0 si x2 = 1/3 soit x= ±1/3½~±0,58.
f(1/3½) =6*(1/ 3½)3-2*1 /3½= -4*3½/ 9.
f(-1/3½) = 6*(-1/ 3½)3+2*3½= +4*3½ / 9
Point d'inflexion : f "(x) = 12 x.
La dérivée seconde s'annule en x= 0 et change de signe.

  
menu