Pour
d�polluer l’air, on utilise un appareil qui fonctionne selon le
principe de la pr�cipitation �lectrostatique :
des poussi�res mais aussi des bact�ries ou des virus pr�sents dans
l’air sont ionis�s (on les charge
�lectriquement), puis collect�s sur des plaques m�talliques gr�ce � un
champ �lectrique qui r�gne entre elles.
Il reste alors � nettoyer les plaques r�guli�rement. Ce proc�d� est
capable d’�liminer jusqu’� 98% des
particules en suspension dans l’air.
On consid�re deux plaques G et D de longueur L=30 cm
espac�es d’une distance 2d = 5,0 cm.
Dans le rep�re (O, i, j ), on �tudie le mouvement d’une
particule charg�e positivement avec une charge
q= 1,6�10
-19 C et une masse m = 10
−18 kg.
A l’instant initial, elle arrive en O (origine du rep�re) avec une
vitesse initiale v
0 = 2,0 m.s
-1. Le
champ �lectrique E qui r�gne entre les plaques est uniforme
et perpendiculaire � celles-ci ; sa norme vaut E =10
5 N/C.
Dans tout l’exercice, on n�glige l’influence du poids de la
particule.
1- Sachant que la particule est soumise � la seule force �lectrique , choisir quel champ
�lectrique va induire un mouvement
de la particule vers la plaque de droite D
.
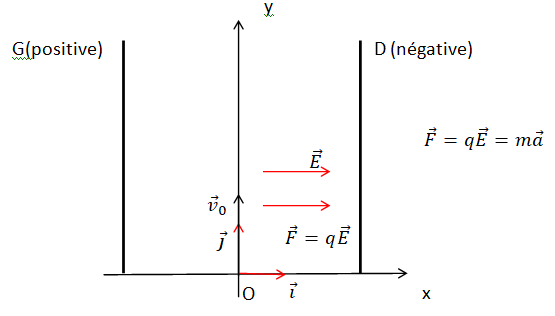
I-2- On suppose que la particule a un mouvement vers la plaque D.
Quelle est la polarit� de la plaque D ?
La plaque D est n�gative.
I-3- Ecrire la 2e loi de Newton pour la particule sous forme
vectorielle.
I-4- En d�duire les composantes du vecteur acc�l�ration.
a
x = qE /m ; a
y = 0.
I-5- Donner les composantes de la vitesse de la particule.
Le vecteur vitesse est une primitive du vecteur acc�l�ration.
v
x = qE / m t + cste.
A t = 0, v
x=0 ;
vx = qE / m t .
vy = cste= v0.
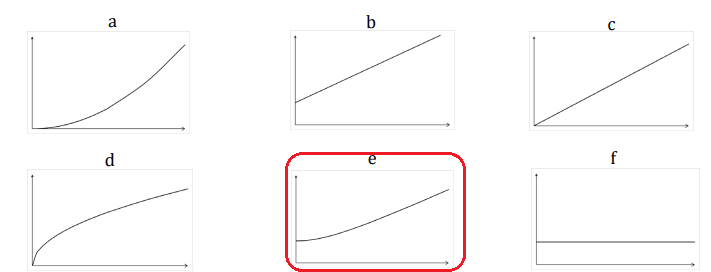
I-6- Parmi les six graphiques ci-dessous cocher sur le document r�ponse
celui qui d�crit l’�volution de
la norme de la vitesse de la particule au cours du temps.
v = (v
x2 +v
y2)
� =
((qE/ mt2 +v02)� .
La vitesse initiale n'est pas nulle : a, c et d ne conviennent pas.
La vitesse n'est pas constante : f ne convient pas.
La vitesse n'est pas une fonction affine du temps : b ne convient pas.
I-7- Donner l’expression des �quations horaires de la particule x(t) et y(t).
La position est une primitive de la vitesse et la position initiale est
l'origine du rep�re ( les constantes d'int�gration seront donc nulles).
x= �qE / m t
2. y = v
0t.
I-8- En d�duire l’�quation de la trajectoire y(x).
t = y / v
0 ; repport dans x :
x =
�qE / (mv02) y2.
y =[2mv02 x/ (qE)]�.
I-9- On nomme C le point d’impact de la particule sur la plaque. Donner l’expression puis la valeur de la
hauteur du point C.
yC =[2mv02 d/ (qE)]�.
yC =[2x 10-18x4 x2,5 10-2/ (1,6 10-19 x105)]�=0,0035 m = 3,5 mm.
I-10- Choisir la bonne r�ponse des propositions suivantes :
Si la masse de la particule double, alors la hauteur de C double aussi. Faux.
y
C est proportionnelle � la racine carr�e de la masse.
Si la masse de la particule double, alors la particule mettra 4 fois plus de temps pour arriver en C. Faux.
x= �qE / m t2.
x �tant inchang�, si m double alors t2 double.
Pour une m�me particule, si sa vitesse initiale est 4 fois plus grande, alors le point C est 2 fois plus haut. Faux.
yC =[2m d/ (qE)]�v0.
Les autres grandeurs restant constantes, yC et v0 sont proportionnelles.
Si le champ �lectrique est 4 fois plus petit, la particule met deux fois plus de temps pour arriver en C.
Vrai.
x= �qE / m t2.
Si le champ �lectrique est 4 fois plus grand, la hauteur du point C sera deux fois plus grande. Faux.
y
C est inversemment proportionnel � la racine carr�e de E.
