Deux
gaz, supposés parfaits, sont enfermés dans deux compartiments (1) et
(2) séparés par un piston mobile athermane (on dit aussi calorifugé)
qui coulisse sans frottement. Le compartiment (1) est entièrement
calorifugé tandis que le compartiment (2) peut échanger de l’énergie
par chaleur (transfert thermique) avec le milieu extérieur, assimilé à
un thermostat de température T
0, à travers une paroi diathermane (non
calorifugée). Les deux compartiments contiennent chacun n moles de gaz et sont, dans l’état initial, à la température T
0. Le volume total des deux compartiments est V
t = 2V
0,
V0 désignant les volumes, initialement égaux, de chacun des deux compartiments.
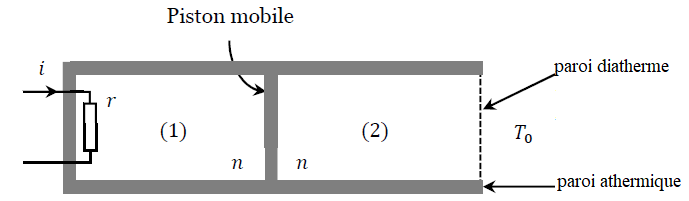
À un instant pris comme origine temporelle, le compartiment (1) reçoit
de la chaleur par l’intermédiaire d’un résistor (résistance r) alimenté
pendant une durée
t,
par un générateur qui délivre un courant d’intensité i constante.
L’état final est l’état d’équilibre thermodynamique du système qui
succède à ce chauffage. On le caractérise par les variables d’état p
k, V
k et T
k qui représentent les pressions, volumes et températures des compartiments (k) où k = 1 ou 2. On note
g la constante des gaz parfaits et
g = C
pm / C
vm.
le rapport de la capacité thermique molaire à pression constante sur la capacité thermique molaire
à volume constant, identique pour les gaz des deux compartiments.
31. Exprimer V
1 et V
2 :
A) V
1 = T
1 V
0 / (T
0+T
1).
B) V1 = T1 Vt / (T0+T1). Vrai.
C)
V2 = T0 V0 / (T0+T1).
D) V2 = T0 Vt / (T0+T1). Vrai.
Equation des gaz parfaits : p1V1 = nRT1 et p2V2 = nRT2 avec T2 = T0 à l'équilibre thermique.
L'équilibre mécanique conduit à p1 = p2.
nRT1 / V1 = nRT0 / V2 ; V1 =T1V2 / T0 = T1(Vt -V1)/ T0 ;
V1 (1+T1 / T0)= T1 / T0 Vt.
V1 =T1 /(T1+T0) Vt.
V2 = Vt-V1 = Vt-T1 /(T1+T0) Vt = T0 /(T1+T0) Vt.
32. Que peut-on affirmer ?
A) p2 = p1. Vrai (
équilibre mécanique)
B) p1 = nR(T0+T1) / Vt. Vrai.
C)
p1 = nR(T0+T1) / V0.
D) p
2 ≠ p
1.
p
1 = nRT
1 / V
1 ;
V1 =T1 /(T1+T0) Vt ;
p1 = nR(T1+T0) / Vt.
33. Déterminer la variation d’énergie interne
DU entre l’état initial et l’état final du système constitué par les deux gaz (on indique que
DU est la somme des variations des énergies internes des deux gaz, entre l’état initial et final) :
A)
DU = 0
B) DU =nR(T1-T0) / (g-1). Vrai.
C)
DU =nRg(T1-T0) / (g-1).
D)
DU =nR(T1-T0) .
La température du gaz (2) ne change pas, donc DU2 = 0.
DU =DU1 =n Cvm DT ; Cpm- Cvm= R ; gCvm - Cvm+= R ; Cvm= R /(g-1)
DU =nR(T1-T0) / (g-1).
34. On note W2 et Q2
le travail et la chaleur (transfert thermique) algébriquement reçus par
le gaz du compartiment (2) entre l’état initial et l’état final. On
supposera la transformation réversible. Que peut-on affirmer ?
A) W2 = nRT0 ln[(T0+T1) / (2T0)]. Vrai.
B) W2 = 0.
C) Q2 = 0.
D) Q2 = -W2. Vrai.
Travail des forces de pression lors d'une tranformation réversible :
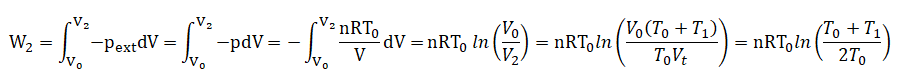
DU2=Q2 +W2 =0. Q2 = - W2.
35. On note Q1 la chaleur (transfert thermique) algébriquement reçu par le gaz du compartiment (1) entre l’état initial et
l’état final. Que peut-on affirmer ?
A) Q1 = DU.
B) Q1 = DU + W2. Vrai.
C) Q1 = W2.
D) Q1 = r i2t. Vrai.
W1 = - W2 ; DU = DU1 =Q1+W1 = Q1-W2 .
36. On note S2(r) l’entropie algébriquement reçue et S2(c) l’entropie algébriquement créée, entre l’état initial et l’état final,
pour le gaz situé dans le compartiment (2). On indique que sa variation d’entropie DS2 entre l’état initial et l’état final
s’écrit DS2 = nR ln (V2 / V0). Exprimer S2(r) et S2(c) :
A) S2(r) = nR ln [2T0/(T0+T1)] Vrai
B) S2(r) = 0.
C) S2(c) = nR ln [2T0/(T0+T1)].
D) S2(c) = 0. Vrai
S2(c) =Q2 / T0 = -W2 / T0 = -nR ln[(T0+T1) / (2T0)] = nR ln[(T0+T1) / (2T0)].
DS2 = S2(c) + S2(r) ; S2(r) = nR ln[(2T0) /(T0+T1) ]- nR ln[(2T0) /(T0+T1) ] =0.