Physique : lunette astronomique, ENAC pilote 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Une lunette astronomique est utilisée pour observer les étoiles. On l’assimile à un système de deux lentilles minces convergentes L1 et L2 de centres respectifs O1 et O2, de même axe optique, et de distances focales images respectives f '1 positive et f '2 positive. L’oeil, supposé emmétrope (c’est-à-dire sans défaut), est placé juste derrière l’oculaire. On note dm = 25 cm la distance entre l’oeil et son punctum proximum, c’est-à-dire la distance minimale de vision nette. Dans tout l’exercice, on admet que les conditions de Gauss sont satisfaites. 25. Que peut-on affirmer ? A) La limite de résolution angulaire d’un oeil normal est d’environ 1,5'. Pouvoir de résolution de l'oeil ~1' une minute d'arc. B) Pour observer nettement l’image à travers l’instrument sans accommoder, le plan focal image de L1 doit coïncider avec le plan focal image de L2. C) Pour observer nettement l’image à travers l’instrument sans accommoder, le plan focal image de L1 doit coïncider avec le plan focal objet de L2. Vrai. D) Si le plan focal image de L1 ne coïncide pas avec le plan focal objet de L2, il est possible que l’oeil emmétrope puisse observer nettement l’image à travers l’instrument. Vrai. L'oeil peut accommoder.   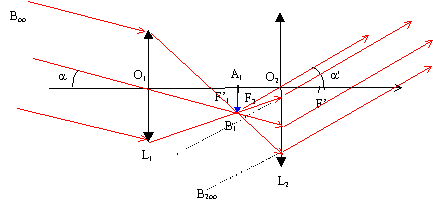26. On observe une étoile située à l’infini en dehors de l’axe optique, sous un angle d’incidence a > 0. La lunette est réglée de telle sorte que l’oeil voit nettement l’étoile sans accommoder. Les rayons lumineux émergent de la lunette sous un angle a' < 0. Exprimer G = a' / a. A) G = -f '2 / f '1 ; B) G = -f '1 / f '2 vrai ;  C) G = -f '1 / dm ; D) G = -dm / f '2. Triangle O2F '1B1 : tan a' = -A1B1/O2F2 ~- a' . L'angle étant petit , on confond la tangente avec l'angle en radian. Triangle O1F '1B1 : tan a = A1B1/O1F1 ~ a . Grossissement G = a' / a = -O1F1 /O2F2 = -f '1 / f '2.   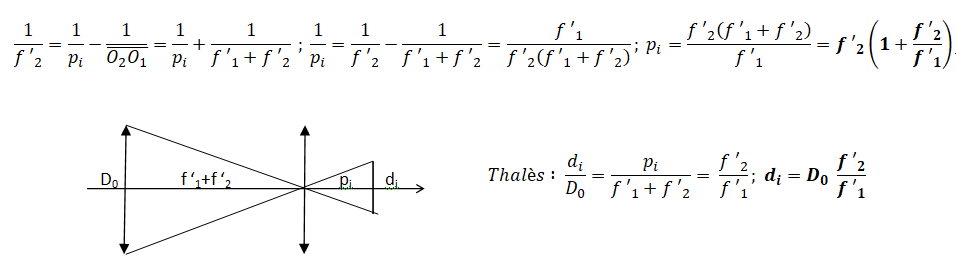27. On note D0 le diamètre de l’objectif L1, ce dernier constituant un objet pour l’oculaire L2. Quel est alors le diamètre di du disque image de l’objectif par l’oculaire, et à quelle distance pi de O2 cette image se forme-t-elle ? A. di = f '2D0 / f '1 vrai ; B. di = f '1D0 / f '2 ; C. pi = f '1( f '1 + f ' 2) / (f '1 +2 f '2)  ; D. pi = f '2( 1 + f ' 2 / f '1). Vrai. ... ....   28  De quelle distance maximale x > 0 peut-on rapprocher l’oculaire de l’objectif, l’oeil étant toujours situé juste derrière l’oculaire, pour pouvoir encore observer l’étoile ? L'image finale n'est plus à l'infini, elle doit se trouver à la distance minimale de vision nette dm. L'image intermédiaire se trouve toujours au foyer image de L1 soit à f '2-x de O2. Réponse A. 29. La lunette est à nouveau réglée dans une configuration d’instrument afocal (l’oeil étant toujours situé juste derrière l’oculaire). On observe alors un objet ponctuel A à distance finie de l’objectif de la lunette sur l’axe optique. On note B l’image de A par L1 et C celle de B par L2. Que peut-on affirmer ? Ecrire la relation de Newton pour l'objectif et pour l'oculaire : Réponses A et D. 30. En déduire la distance minimale Dmin  à laquelle on peut placer A pour que l’oeil puisse observer nettement l’image de A à travers la lunette ?

menu