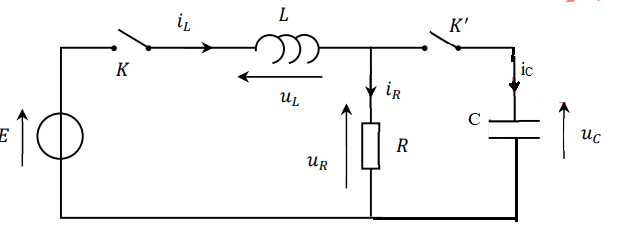
Physique : Transitoire d'un RLC, régime forcé, concours ENAC pilote 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Transitoire d'un RLC. Dans le circuit LRC représenté sur la figure ci-après, les interrupteurs K et K' sont initialement ouverts. On désigne respectivement par uR, uL et uC, les tensions aux bornes du résistor de résistance R, de la bobine d’inductance L et du condensateur de capacité C. On note iR, iL et iC les intensités du courant électrique qui traversent respectivement ces dipôles. Le générateur est idéal, de tension électromotrice E (on dit aussi force électromotrice) stationnaire. Le condensateur est initialement chargé de sorte que uC= E /3.   13. À un instant prix comme origine temporelle, on ferme K ( K' restant ouvert). Que peut-on dire, à l’instant t= 0+, de uR(0+) et de uL(0+) ? A) uR(0+) = 0 vrai ; B) uR(0+) =E ;  C) uL(0+) = 0 ; D)  uL(0+) = E vrai. Continuité de l'intensité iL(0+) = iR (0+)=) 0= iL(0) = iR (0)=0. Additivité des tensions : E = uR(0+) +uL(0+)= 0 + uL(0+).  14. Comment évoluent iL(t) et uL(t) ?  A) iL(t) = E / R(1 − exp(-R /L t)) vrai ;  A) iL(t) = E / R exp(-R /L t) ; C) uL(t) = E (1 − exp(-R /L t)) ; D) uL(t) = E exp(-R /L t) vrai. E =uL(t) +uR(t). uR(t)= R iL(t) ; uL(t)=LdiL(t) /dt. E = R iL(t) +LdiL(t) /dt. (1). Solution de R iL(t) +LdiL(t) /dt = 0 : iL(t) = A exp(-R /L t) avec A une constante. Solution particulière de  (1) : iL(t) = E / R. Solution générale de (1) : iL(t) = A exp(-R /L t) +E / R. iL(0) = 0 d'où A = -E / R. uL(t) = LdiL(t) /dt = E exp(-R /L t).  15. On attend suffisamment longtemps pour que le régime précédent s’achève (on dit aussi qu’il atteint le régime permanent), puis on ferme le second interrupteur K' à un instant pris comme nouvelle origine temporelle. Déterminer iL(0+) et iR(0+) :  A) iL(0+)= 0 ; B) iL(0+)=E / R vrai  ; C) iR(0+)=2E /(3R) ;  D)  iR(0+)=E /(3R) vrai. iL(t) = A exp(-R /L t) +E / R. Quand t devient grand ( régime permanent), l'intensité  iL(t) tend vers E / R. Continuité de l'intensité dans la bobine : iL(0) = iL(0+) = E / R. uR(0+)= uC(0+) = E / 3. uR(0+)= RiR(0+). iR(0+)=E /(3R). 16. Déterminer iC(0+) et uL(0+) : A) iC(0+) = 0 ; B) iC(0+)=2E / (3R) vrai ; C) uL(0+)=2E /3 vrai ;  D) uL(0+) =E / (3R). Loi des noeuds : iC(0+) + iR(0+)= iL(0+)= E / R. iC(0+) =E /R -iR(0+)=E / R -E /(3R) =2E / (3R). Loi des mailles : E = uL(0+) +uR(0+)=uL(0+) +uC(0+)=uL(0+) +E / 3. uL(0+) =2E / 3.  17. Après fermeture de K', l’intensité iL(t) obéit à l’équation différentielle suivante : d2iL / dt2 +1/te diL/dt +w02iL = w02ioo où te, w0 et ioo sont des constantes indépendantes du temps. Exprimer te et w0. A) te=RC vrai ; B) te=L / R ;  C) w0=1 /(LC)½ vrai ; D) w0=R / L. E = LdiL /dt +R(iL-iC)=L diL/dt +RiL-Ric. iC=dq /dt =C duC/dt. uC =E-uL ; duC/dt = -duL/dt = -L d2iL/dt2. E = L diL/dt +RiL+RCL d2iL/dt2. d2iL/dt2+ 1/(RC)diL/dt +1/(LC) iL = E / (RLC). (1) On identifie  : te=RC ; w0=1 /(LC)½ .  18. Exprimer ioo ainsi Ec que l’énergie emmagasinée dans le condensateur lorsque le régime devient stationnaire :   A) ioo= E /(3R) ; B)  ioo= E / R vrai C) Ec=0 ;  D) Ec= CE2 / 2 vrai. Au bout d'un temps très long, la bobine se comporte comme un petit fil ; la solution particulière de l'équation (1) est ioo =E / R. La tension aux bornes du condensateur est égale à E. ... .... Un générateur de résistance interne ri délivre des signaux sinusoïdaux e(t), de pulsation w, et d’amplitude complexe em =em , ici réelle (phase à l’origine nulle). Ce générateur alimente un circuit série constitué d’une bobine d’inductance L et de résistance rL, d’un résistor de résistance R et d’un condensateur de capacité C. Le circuit est étudié en régime établi (dit aussi permanent). On note uL m et uC m les amplitudes complexes des tensions ue aux bornes de la bobine et uC aux bornes du condensateur respectivement. On désigne par u e m l’amplitude complexe de la tension ue aux bornes du générateur, et i m, celle de l’intensité i du courant dans le circuit.   19. 20  Le rapport des amplitudes complexes u c m /  u e m se met sous la forme suivante : u c m /  u e m =H0 / [ 1 +jw/Q-w2) avec x = w / w0 où H0, Q et w0 sont des constantes indépendantes de w, j est ’'unité imaginaire (j2 = −1). Exprimer H0 et w0 et Q. A) H0 = 1 Vrai  B) H0 = (R+rL) /( (R+rL+ri) C) w0 = 1 / (RC)  D) w0 = 1 / (LC)½. Vrai Le pont diviseur de ternsion conduit à : 21. On suppose désormais, jusqu’à la fin de l’exercice, que w = w0. Quelle relation existe-t-il alors entre u em et em A. u em =R / (R +rL+ri) em B. u em =R / (R +rL )em. C. u em =(R + RL)/ (R +rL+ri) em. D. u em = em. 22. Déterminer im et uCm. A)   im=em /(R+rL) ; B)  im = em /(R+rL+ri) vrai ; C) uCm =-jQH0 uem;  D) uCm =.jQH0 uem vrai.   23. L’amplitude complexe uLm s’écrit alors uLm = (a+jb)em où a et b sont des constantes qui ne dépendent que des caractéristiques du circuit. Déterminer a : A) a = rL / (R+rL+ri) vrai ; B)  a = rL / (R+rL) ; C) a = ri / (R+rL+ri) ; D) a =1.   24. Déterminer b : A) b=0;  B) b=1 ; C) b = (L / C)½ x 1/ ((R+rL+ri) vrai; D) b= 1 / Q.

menu