Physique : cinématique, templin de saut à ski, concours ENAC pilote 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Cinématique. 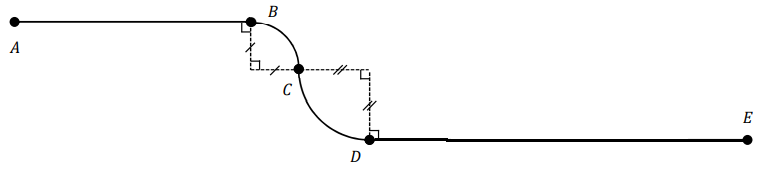On étudie un mobile , assimilé à un point matériel (ou corpuscule), en mouvement uniforme dans le référentiel du laboratoire à la vitesse de 25 cm / s, sur une piste qui comporte quatre portions : - un segment rectiligne AB de longueur 1 m ; - un quart de cercle BC de longueur 50 cm ; - un quart de cercle CD de longueur 75 cm ;  - un segment rectiligne DE de longueur 2 m. La piste est parcourue par M de A vers E.  1. Quelle durée met M pour parcourir la totalité de la piste (de A à E ) ?  A) = 0,17 s ; B) = 1,6 s ; C) = 17 s vrai ; D) = 160 s. Longueur de la piste : 1 +0,75 +0,50 +2 = 4,25 m. Le mouvement étant uniforme ( norme de la vitesse constante ), la durée est égale à : 4,25 / 0,25 = 17 s.  2. On note a1 la norme de l’accélération de M sur la portion BC. Que vaut a1 ?  A) = 0 m. s-2 ; B) = 0,2 m. s-2 vrai ;  C) = 1,3 m. s-2 ;  D) = 13 m. s-2. Accélération centripète de norme v2  / R avec R = 4BC / (2p) =2 /(2 x3,14) =0,318 m. a1 = 0,252 / 0,318 ~0,2 m. s-2 . 3. On note a2 la norme  de l’accélération de sur la portion CD. Quelle relation existe-t-il entre a1 et a2 ?  A) = 0  B) a1 = a2 ; C) a2 =2 / 3 a1 vrai ;  D)  a2 =1,5 a1 . Accélération centripète de norme v2  / R avec R = 4CD / (2p) =3 /(2 x3,14) =0,478 m. a2 = 0,252 / 0,478 ~0,13 m. s-2 soit 2 / 3 a1. 4.  Lorsque M atteint le point D , à un instant pris comme origine temporelle, un second mobile (également assimilé à un point matériel) quitte E en direction de D. Son mouvement est uniforme dans le référentiel du laboratoire à la vitesse de 50 cm / s. À quelle date les deux mobiles se rencontrent-ils ? A) ≈ 0,4 s  ; B) ≈ 2,7 s vrai ; C) ≈ 4 s ; D) ≈ 8 s . M atteint le point D à la date t =2,25 / 0,25 =9 s. Mouvement ultérieur de M : x1 = 0,25 t. Mouvement du second mobile : x2 = - 0,50 t + 2. A la rencontre : 0,25 t = -0,50 t +2 ; t = 2 / 0,75 =8 /3 ~ 2,7 s.  5. Quelle est alors la distance parcourue par M sur la piste DE?  A) ≈ 40 cm ; B) ≈ 67 cm vrai ; C) ≈ 1 m ; D) ≈ 1,5 m. 0,25 x 2 / 0,75 ~0,67 m =2 /3 ~ 0,67 m =67 cm. 6. Quelle était, 0,2 s avant la rencontre, la distance séparant les deux mobiles ?  A) ≈ 5 cm ; B) ≈ 10 cm ; C) ≈ 15 cm vrai ; D) ≈ 50 cm. x1= 0,25 (2,667-0,2) =0,617 m. x2=  -0,5 x(2,667-0,2)+2 =0,766 m et se trouve à 0,75 m de D. 0,766 -0,617 ~0,15 m ~15 cm. ... .... Tremplin de saut à ski. Un tremplin de saut à ski est constitué par l’association d’une portion rectiligne L= AB= 40 m de piste inclinée d’un angle a= 30° par rapport à l’horizontale, suivie par une portion circulaire BO de centre O' et de rayon R= 20 m. La tangente en O à la piste circulaire forme un angle ß= 45° avec l’horizontale. Le point C sur la piste circulaire est situé au-dessous et à la verticale de O'.  On étudie le mouvement d’un skieur, initialement immobile en A, en l’assimilant à un corpuscule (ou « point matériel) de masse m= 80 kg, de coordonnées cartésiennes (x,  z). On néglige tout frottement. On prendra g = 10 m s-2. Exprimer puis calculer numériquement la vitesse du skieur en B.  A) vB = [3½gL]½ ;  B) vB = [2gLsin a]½ vrai ; C) vB= 20 m./s vrai ; D) vB= 13 m./s. Entre A et B le skieur est soumis à son poids et à l'action normale du plan. Travail moteur du poids entre A et B : m g L sin a. Le travail de l'action normale du plan est nul. Théorème de l'énergie cinétique entre A et B : ½mvB2 -0 = m g L sin a. vB2  = 2 g L sin a = 2 x10 x40 x 0,5 =400: vB ~20 m /s.  7. On note a le vecteur accélération du skieur au point C. Que peut-on affirmer :  8. On choisit l’origine de l’énergie potentielle de pesanteur en O. Exprimer l’énergie potentielle de pesanteur Ep(B) en B du skieur : A) mgb( sin ß-sin a) ;  B) mgb( cos ß +cos a) ; C) mgb( sins ß -cos a) ; D) mgb( cos ß -cos a). Vrai. O'H = b cos ß ; O'K = b cos a ; HK = b (cos a -cos ß) > 0. B est en dessous de O, l'énergie potentielle en B est négative. Ep(B) = -mg HK = mgb( cos ß -cos a). 9. Que dire de la norme du vecteur vitesse, vO, du skieur en O? A)  vO=[vB2 -2Ep(B) / m]½ ; B) v0 = vB ; C) vO=[vB2 +2Ep(B) / m]½ vrai ; D) v0 > vB . Conservation de l'énergie mécanique entre B et O : ½mvB2 +Ep(B) = ½mvO2. vB2 +2Ep(B) / m = vO2.  10. Le skieur quitte le tremplin en O. On note F le sommet de sa trajectoire. En tenant compte de la valeur numérique de ß, quelle est l’altitude zF de F ? A) v02 /g ; B)  v02 / (2g) ; C) v02 / (4g) vrai ; D) 2v02 / g. Conservation de l'énergie mécanique entre F et O : ½mvF2 +Ep(F) = ½mvO2. En F la vitesse est horizontale et vaut vO cos ß. ½mvO2 cos2ß +mg zF = ½mvO2. zF =vO2(1-cos2ß ) / (2g). cos245 =0,5 . zF =vO2 / (4g).    11. Un autre skieur, moins aguerri, se retrouve confiné au voisinage de C et oscille, d’avant en arrière, dans un mouvement de très faible amplitude. Quelle est la période Tde ses oscillations ? A) T=(b / g)½ ;  B) T= 2p (b / g)½ vrai ; C) T≈ 9 s vrai ; D) T= 1,5 s. On note M la position de ce skieur. Il s'agit de l'équation d'un oscillateur harmonique de pulsation w = (g / b)½. T= 2p (b / g)½ =2 x3,14x(20 / 10)½ ~9 s.

menu