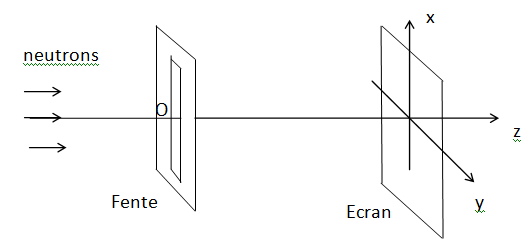
Dans
l’exp�rience de Zeilinger men�e au laboratoire Laue-Langevin de
Grenoble en 1988, on envoie des neutrons (masse
𝑚 ≈ 1,7 � 10
-27 kg sur une fente de largeur e = 90 �m. Le
plan de la fente est perpendiculaire � la direction (axe Oz) des
neutrons. Les neutrons envoy�s ont une vitesse v = 0,2 km. s
-1.
On rappelle la valeur approximative de la
constante de Planck, h ≈ 6,6 � 10
-34 SI. On n�glige
l’influence du champ de pesanteur terrestre.
31. Quelle(s)
unit�(s), dans le Syst�me International, peut-on attribuer � h ?
A) Joule par
seconde (J.s
-1) ;
B) Joule seconde
(J. s)
vrai ;
C) Joule (J)
;
D) Kilogramme m�tre
carr� par seconde (kg. m
-2
. 𝑠
-1)
vrai.
E (joule) = h x fr�quence ( s
-1).
Or 1 joule = 1 N m = 1 kg m
2 s
-2.
h s'exprime en kg m
2 s
-1.
32. Donner la
valeur de la longueur d’onde de De Broglie
l d’un neutron.
A) ≈ 2 nm
vrai ;
B) ≈ 200 nm ;
C) ≈ 2 �m ;
D) ≈ 20 nm.
l = h
/ (mv) =6,6 10
-34 /(1,7 10
-27 x200)~ 2 10
-9
m ~ 2 nm.
33. On place
un �cran derri�re la fente, parall�lement � son plan, � une distance D
= 5 m. Pour cette valeur,
on admet qu’on se trouve, avec une excellente approximation, dans une
situation de diffraction � l’infini. Cette
diffraction s’effectue selon la direction Oy. Quelle est l’expression
de l’�chelle angulaire
q
caract�risant cette exp�rience
de diffraction de neutrons ?
A) sin
q ~
l / e.
Vrai B) sin
q ~e /
l.
C) sin
q ~
l / D.
D) sin
q =D /
l.
34. Calculer la
valeur de
q. On
exprimera cette valeur en secondes d’arc (′′).
A) 4 10
-3.
B) 4 10
-2.
C) 0,4.
D) 4.
Vrai.
l / e
= 2 10
-9 / (90 10
-6) = 2,22 10
-5 ;
q =2,22 10
-5 rad
~2,22 10
-5 x180 / 3,14 ~0,00127 degr� = 0,00127 x3600 ~4,6 ".
35. La valeur
pr�c�dente de
q
correspond au premier minimum de la figure de diffraction observ�e sur
l’�cran. Quelle est
la position 𝑦
1 > 0 de ce premier minimum ?
A) ~100 nm.
B) ~1 �
m.
C) ~10 �
m.
D) ~100 �
m.
Vrai.
tan
q ~
q =y
1 / D ; y
1
=D
q ~ 5,0 x2,2 10
-5
~1,1 0
-4 m ~100 �m.
36. On
reprend maintenant cette exp�rience de comptage de neutrons de la fa�on
suivante : au lieu d’envoyer un tr�s grand
nombre (𝑁 ≫ 1) de neutrons en une seule fois sur une dur�e tr�s br�ve,
on r�alise une exp�rience de diffraction neutron
par neutron. Pr�cis�ment, on envoie de fa�on r�p�t�e (𝑁 ≫ 1 fois),
avec une p�riode de r�p�tition T suffisamment
�lev�e, un neutron. � chaque r�p�tition, le neutron envoy� est
ind�pendant de celui envoy� juste avant. La figure ci-dessous, qui
est le r�sultat d’une simulation num�rique reproduisant cette
exp�rience de diffraction, montre l’�volution de la
distribution des impacts des neutrons sur l’�cran pour quatre valeurs
de 𝑁. Donner les affirmations exactes parmi celles
ci-dessous.
A) La position d’un
seul impact est compl�tement impr�dictible et, au fur et � mesure que
l’on envoie des neutrons
ind�pendants, on reconstruit progressivement la figure de diffraction
attendue.
Vrai.
B) Si la source qui �met
les neutrons un par un se trouve � 5 m de la fente diffractante, il est
indispensable d’avoir T > 50 ms pour �tre s�r de r�aliser une
exp�rience neutron par neutron.
Vrai.
T > D / v ; T > 5 /200 ; T > 25 ms.
C) Cette
exp�rience ne donnerait pas des r�sultats analogues si elle �tait
r�alis�e avec de la lumi�re.
Faux.
On peut r�aliser une exp�rience de diffraction des photons (
q et
l seraient diff�rents )et
obtenir le m�me constat.
D) La position d’un seul
impact n’est pas compl�tement impr�dictible.
Faux.
