On
considère un corpuscule A (masse m) soumis à une force centrale
attractive caractérisée par une énergie potentielle E(r), r étant la
distance de A au centre attracteur C. Ce dernier est l’origine d’un
référentiel R supposé galiléen. La force
s’écrit :
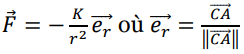
𝐾 est une constante positive.
25. Quelle est la forme de E(r)si son origine est prise pour A et C infiniment éloignés l’un de l’autre ?
A) E(r) = -Kr
2 ;
B) E(r) = -Kr
-1 vrai ;
C) E(r) = ½Kr
-1 ;
D) E(r) = Kr
-2 .
L'énergie potentielle est définie par :
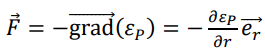
Par intégration E
p = - K / r + cste.
Si r tend vers plus l'infini, E
p tend vers zéro ; la constante est nulle.
26. On note
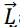
le moment cinétique, dans R, de 𝐴 au point 𝐶. Que peut-on dire de l’évolution temporelle de ce vecteur au cours du
mouvement de 𝐴 ?
A) Ce vecteur moment cinétique change de direction mais sa norme est constante.
B) Ce vecteur moment cinétique ne change pas de direction et sa norme varie.
C) Ce vecteur moment cinétique est une constante vectorielle.
Vrai.
D) La norme et la direction de ce vecteur moment cinétique ne sont pas constantes.
Ecrire le théorème du moment cinétique :
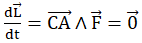
car ces deux vecteurs sont colinéaires.
Le vecteur moment cinétique est donc un vecteur constant.
27. Quelle est l’expression de l’énergie mécanique E
m de A ?
A) E
m = ½m r'
2+ L
2 / (2m r
2) -K / r.
Vrai.
B) E
m = ½m r'
2+ L / (2m r
2) -K / r.
C) E
m = ½m r'
2+ L
2 / (2m r
2) +K / (2r).
D) E
m = ½m r'
2- L
2 / (2m r
2) -K / r.
Le mouvement s'effectue dans le plan perpendiculaire au vecteur moment cinétique.
En coordonnées cylindriques :
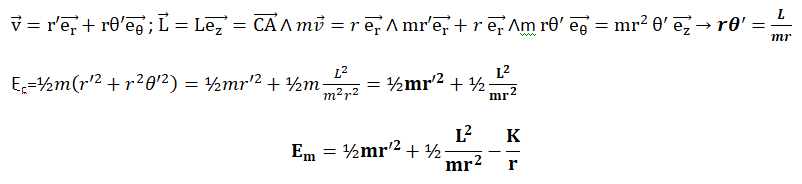 28.
28. A propos du vecteur
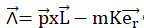
?
On note p la quantité de mouvement.
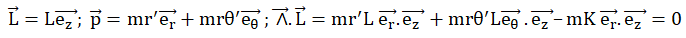
Réponse
A
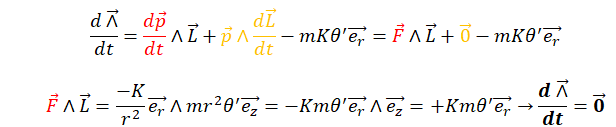
Réponse
B
29. Le corpuscule 𝐴 est un satellite qui effectue des révolutions circulaires, de rayon R, autour du centre C de la Terre.
Quelle est la norme v de la vitesse de A et quelle égalité relie son énergie cinétique et son énergie potentielle ?
A) v=[K /(mR)]
½.
Vrai.
B) v=[K / (mR)]
2.
C) E
m=E
p / 2.
D) E
m= -E
p / 2.
Vrai.
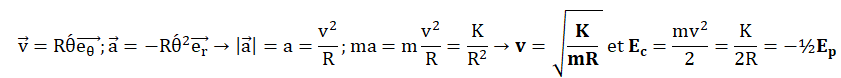 30.
30. Le satellite rentre dans l’atmosphère terrestre et est alors soumis à une force de frottement. Identifier les affirmations
exactes.
A) En moyenne sur une révolution, le satellite ralentit.
B) Le vecteur représentant la force de frottement est de sens opposé au vecteur vitesse de A.
Tout dépen de de la forme
du satellite : il existe une force de trainée, opposée à la vitesse et
une force de portance, perpendiculaire à la vitesse.
C) La norme de l’accélération du satellite augmente au cours du temps.
D) Le moment cinétique de A est toujours une constante vectorielle.
Faux.
L'énergie mécanique diminue : dEm /dt = mv dv/dt +K / r2 r' < 0 ; donc r diminue, ou v diminue ou r et v diminuent.