Un
faisceau de lumière parallèle, modélisé par un cylindre de diamètre D
i
, passe dans un système optique S constitué
par trois lentilles minces L
1, L
2 et L
3, dans cet ordre. Le faisceau est parallèle à l’axe optique de S. Les
lentilles ont,
respectivement, une distance focale image f
1 > 0, f
2 < 0 et f
3
> 0 ; leur centre optique respectif est noté O
1
,O
2 et O
3. À la
sortie de S, le faisceau est toujours cylindrique, parallèle à l’axe
optique, mais de diamètre D
f.
Le sens positif étant celui de la
lumière incidente. En outre, dans tout l’exercice, on admet
que les conditions de Gauss sont satisfaites.
7. Que peut-on dire de S ?
A) S est convergent.
B) S est afocal.
Vrai.
C) S est divergent.
D) On ne peut rien dire a priori.
Les rayons incidents et émergents son parallèles à l'axe optique.
L'image d'un objet à l'infini est à l'infini. Le système est donc
afocal.
8. Parmi les affirmations suivantes, lesquelles sont exactes ?
A) On ne pourrait pas élargir le faisceau avec un système optique formé
uniquement de L
1 suivie de L
2.
Vrai.
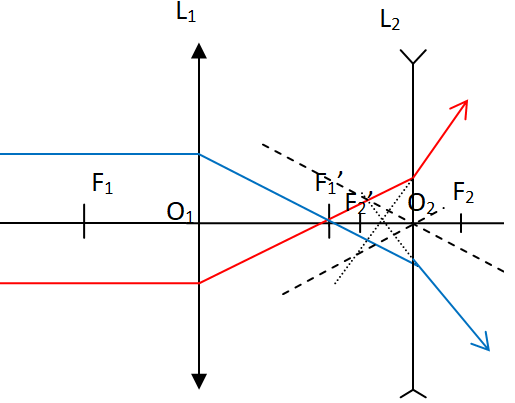
Le faisceau émergnet n'est pas parallèle à l'axe optique.
B) Avec le système formé uniquement de L
1 et L
3
, positionnés de sorte que le foyer objet de L
3 coïncide avec le
foyer image de L
1
, le faisceau sera nécessairement élargi.
Faux.
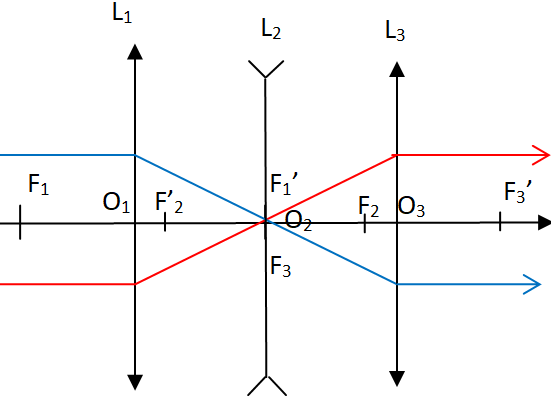 C)
C) Avec le système formé de L
1, L
2 et L
3, on ne peut pas faire un système afocal en plaçant le foyer objet de L
3 au
foyer image de L
1.
L'ensemble L
1, L
3 est afocal ; ajpouter L
2 fait diverger le faisceau , sauf si on la place en F'
1..
D) On ne pourrait pas élargir le faisceau incident en utilisant
uniquement les lentilles L
2 et L
3
.
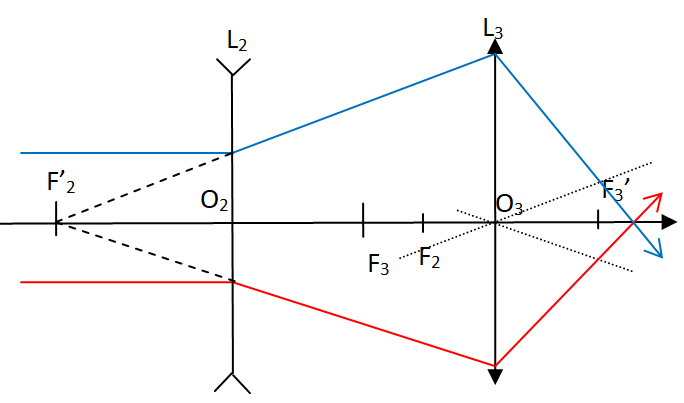
Le faisceau émergent n'est pas parallèle à l'axe optique.