Le
r�f�rentiel du laboratoire est muni d’un rep�re cart�sien. On r�alise
un pendule simple en suspendant une masselotte 𝐴 de masse m = 10 g, �
une tige conductrice de masse n�gligeable devant m et de longueur L = OA = 40 cm. La dimension de la masselotte est
n�gligeable devant L. La liaison pivot du pendule, en O,
est suppos�e parfaite (sans frottement) et permet au pendule d’osciller
dans le plan. La position de la tige est
rep�r�e par l’angle
q, orient� dans le sens direct, qu’elle forme avec
la verticale descendante. La continuit� du circuit est
assur�e par un balai mettant la tige en contact en A avec un guide
circulaire conducteur, lui-m�me reli� � un condensateur
de capacit� C= 1 F. On n�glige toute r�sistance �lectrique dans le
circuit, ce dernier �tant ferm� en O. On note i(t)) l’intensit�
qui circule dans le circuit orient� comme indiqu� sur la figure.
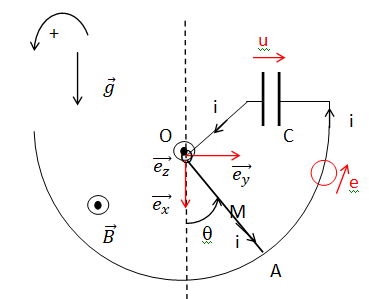
Le balai glisse sans frotter sur le guide. Ce pendule est plac� dans un champ magn�tique uniforme et stationnaire B = 1 T
ሬሬሬ⃗
o� Le pendule, initialement immobile
et formant un angle
q0 > 0 avec la verticale, est abandonn� sans vitesse � l’instant 𝑡 = 0, le condensateur �tant d�charg�.
31. On note
F le flux du champ magn�tique � travers le circuit et
F0
sa valeur particuli�re lorsque
q = 0. En exprimant
F
en fonction notamment de
F0
, d�terminer � l’aide de la loi de Faraday la force �lectromotrice e induite dans le circuit
lors du mouvement du pendule.
A) e
= -�L
2B
q'
.
B) e=�L
2B
q'
.
Vrai.
C) e=L
2B
q'
.
D) e=0,25L
2B
q'
.
Surface du circuit = aire d'une portion de disque + aire de la portion d�limit�e par le condensateur not�e S
0.
S =S
0 +�(
p/2-
q)L
2.
Flux :
F = BS = B(S
0 +�(
p/2-
q)L
2).
Force �lectromotrice e = -d
F /dt = -�BL
2d(
p/2-
q) /dt = +�BL
2d
q /dt =�L
2B
q'
.
32. . �tablir l’expression de l’intensit� du courant �lectrique.
A) i
= �L
2 B C
q'
.
B) i
= �L
2 B C
q".
Vrai.
C) i
= L
2 B C
q'
.
D) i
= -L
2 B C
q".
Tension aux bornes du condensateur u = e.
i = Cdu /dt =Cd(�L
2B
q'
) /dt =�CL
2B
q".
33. Exprimer le moment en O des forces de Laplace qui s’exercent sur la tige OA..
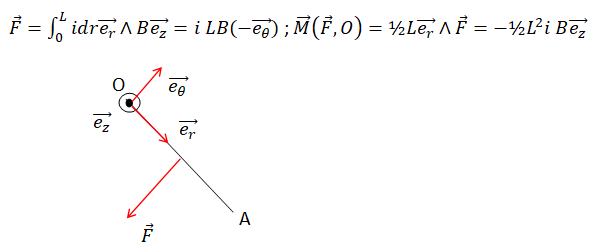
R�ponse
D.
34. L’�quation du mouvement se met sous la forme suivante :
q"̈+
w12 sin
q = 0 o�
w1
est une constante temporelle.
D�terminer
w1.
Ecrire le th�or�me du moment cin�tique :
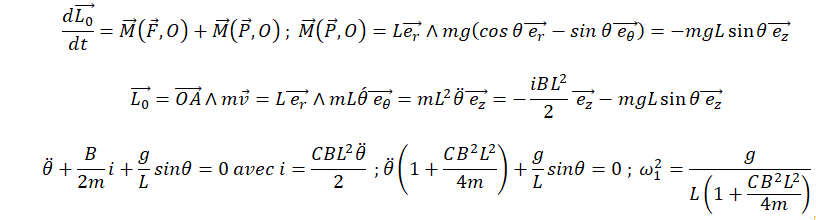
R�ponse
C.
35. On suppose
q0 << 1. L’intensit� du courant �lectrique ob�it � l’�quation suivante : d
2i/dt
2 +
w22i = 0 o�
w2
est une constante
temporelle. D�terminer
w2
.
A) w2
= 0.
B) w2=
w1.
Vrai.
C) w2=2
w1.
D) w2=�
w1.
sin
q ~
q et
q"̈+
w12 sin
q = 0 s'�crit :
q"̈+
w12 q = 0
Or q"̈+
w22 q = 0.
36. Calculer num�riquement
w1
:
A) ~1 rad/s.
B) ~2,3 rad/s.
vrai.
C) ~5 rad/s.
D) ~12 rad/s.
w12 =10 / [0,4(1+0,4
2 / 0,04)]=5 ;
w1 ~2,3 rad / s.
