Forces centrales,  concours ENAC pilote 2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Un satellite artificiel, assimilé à un corpuscule de masse m, est en mouvement circulaire de rayon R autour de la Terre supposée à symétrie sphérique (rayon moyen R ≈ 6400 km, masse M ≈ 6 × 1024 kg). On note T le centre de la Terre.  25. Quelle est, en fonction des coordonnées polaires (r, j) du satellite, l’expression, dans le référentiel géocentrique, du vecteur moment cinétique, au point 𝑇, du satellite ? 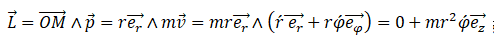Réponse A.   26. Quelle est l’énergie potentielle effective du satellite ? Energie potentielle  de gravitation : Ep = -GMm / r. Energie cinétique : Ec = ½m v2. Energie mécanique Em= ½m v2 -GMm / r= ½m( r'2 +r2 j'2)-GMm / r. Or L = m r2 j '. Em = ½m  r'2 +L2 / (2m r2) -GMm / r. Energie potentielle effective Eeff = L2 / (2m r2) -GMm / r. Réponse C. 27. Le satellite est géostationnaire. Quelle(s) particularité(s) présente le mouvement orbital du satellite ?  A) Le mouvement orbital du satellite est plan. Vrai. B) Le mouvement s’effectue dans un plan contenant l’axe des pôles. C) Le mouvement ne présente aucune caractéristique particulière.  D) Le mouvement s’effectue dans le plan équatorial. Vrai. 28. Le satellite est en orbite basse circulaire à une altitude h = 600 km autour de la Terre. Quelle est l’expression puis la valeur de la vitesse v0 du satellite au cours de son mouvement dans le référentiel géocentrique ? On donne la valeur approximative de la constante de Newton : G ≈ 7 × 10-11 SI (SI = Système International des unités). v = [G M / (R+h)]½ = [7 10-11 x 6 1024 /(6400 +600) 103)]½ = (6 107)½ ~8 103 m /s. Réponses A et C.   29. Quelles sont les éventuelles affirmations exactes concernant les énergies du satellite sur son orbite ?  A) Son énergie mécanique est égale à son énergie cinétique. B) Son énergie mécanique est égale à l’opposé de son énergie cinétique. Vrai. Pour un mouvement circulaire : Ec =½m GM /(R+h) = -½ Ep. Em = Ec + Ep = -½ Ep + Ep =½ Ep = -Ec .  C) Son énergie mécanique est égale à L2 / [2m(R+h)2]. Vrai. v = r j ' ; Ec = ½mv2 =½m r2 j '2 = L2 / [2m(R+h)2].  D) Son énergie mécanique est égale à l’opposé de son énergie potentielle de gravitation. 30. .On peut transposer les résultats ci-dessus concernant un satellite en orbite circulaire, soumis à une force gravitationnelle, à un électron, soumis à la force électrostatique, en orbite circulaire autour d’un proton. Ce modèle de l’atome d’hydrogène est connu sous le nom de modèle de Bohr.  Dans ce modèle, l’orbite électronique est telle que son rayon est un multiple d’une constante fondamentale aB appelée rayon de Bohr : rn = n2aB, où n est un nombre entier naturel différent de zéro.  En outre, le moment cinétique de l’électron par rapport au point O centré sur le proton est, lui aussi, quantifié : L0=n h  où n est le même nombre entier que précédemment et h = h / (2p) , h étant la constante de Planck. Comment s’écrit, dans ce modèle, l’énergie mécanique Em de l’électron ? D'après la question précédente : Em= -Ec = -L2 / [2m(R+h)2]. Em= -(n h)2 / [2m(n2 aB)2] = -  h2 / [2m n2 aB2].  Réponse C.

menu