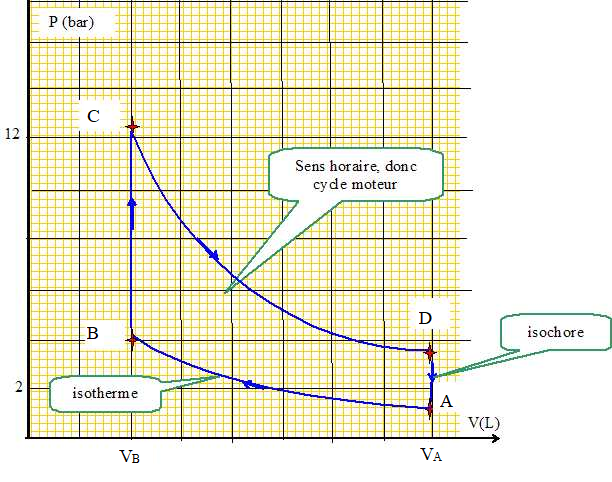
On schématise le fonctionnement d’un moteur de Stirling en considérant qu’un gaz (nombre de moles ), supposé
parfait, évolue selon un cycle de quatre transformations : deux transformations isothermes et deux transformations
isochores. L’isotherme AB est à la température T
1 et l’isotherme CD à la température T
2 > T
1. Le gaz ne subit aucun
changement d’état physique au cours de son cycle.
Lors de la succession des deux transformations DA et AB, le gaz reçoit algébriquement la chaleur (ou transfert thermique) Q
1. De même, lors de la succession des deux transformations BC et CD, le gaz reçoit algébriquement la chaleur (ou transfert
thermique) Q
2.
On note
g le rapport
des capacités thermiques du gaz à pression constante et volume constant respectivement, et R≈ 8 J. K
-1mol
-1 désigne la constante des gaz parfaits.
En outre,V
A et V
B étant les volumes du gaz dans l’état A et B
respectivement, on note a=V
A / V
B
le rapport de compression du gaz.
 19.
19. On note W le travail (transfert mécanique) reçu algébriquement par le gaz sur un cycle de transformations. Quel est le
signe de W et quel est le bilan énergétique du gaz au bout d’un cycle de transformations ?
A) W < 0
vrai ;
B) W >0
;
C) W-Q
1-Q
2=0 ;
D) W+Q
1+Q
2=0
vrai.
Au cours d'un cycle moteur le fluide fournit le travail W < 0 cède la chaleur Q1 à la source froide
et prend la chaleur Q2 à la source
chaude. Au cours de ce cycle l'énergie interne du fluide est nulle :
W+Q
1+Q
2=0.
20. Quelles sont les expressions de Q
1 et Q
2 ?
Transformation isochore DA : W
DA = 0 ; Q
DA =
DU
DA = C
v(T
1-T
2).
Relation de Meyer : C
v =nR /(
g-1).
Q
DA =nR /(
g-1)(T
1-T
2).
DU
AB =0, l'énergie interne d'un gaz parfait ne dépend que de la température.
Q
AB + W
AB = 0 ;
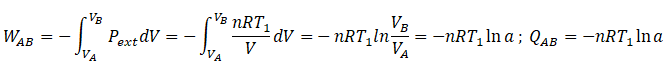 Q1 = QDA +QAB =nR /(g-1)(T1-T2)-nRT1 ln a
Q1 = QDA +QAB =nR /(g-1)(T1-T2)-nRT1 ln a.
Transformation isochore BC : W
BC = 0 ; Q
BC =
DU
BC = C
v(T
2-T1
).
Relation de Meyer : C
v =nR /(
g-1).
Q
BC =nR /(
g-1)(T
2-T
1).
DU
CD =0, l'énergie interne d'un gaz parfait ne dépend que de la température.
Q
CD + W
CD = 0 ;
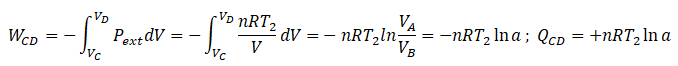 Q2 = QBC +QCD =nR /(g-1)(T2-T1)+nRT2 ln a
Q2 = QBC +QCD =nR /(g-1)(T2-T1)+nRT2 ln a.
Réponse
C.
21. On admet désormais que Q
1 et Q
2 sont respectivement identiques aux chaleurs Q
f et Q
c que le gaz recevrait
algébriquement de la part d’une source froide (température T
f ) et de la part d’une source chaude (température T
c). Ce
faisant, on se ramène à un moteur ditherme. Quelles sont, parmi les affirmations ci-dessous, celles qui sont inexactes ?
A) Pour le gaz, Q
1< 0 et Q
2 > 0.
La source chaude donne de la chaleur au gaz : Q2 > 0. Le gaz cède de la chaleur à la source froide Q1< 0.
B) Le rendement de ce moteur est inférieur à 1.
C) À la fin du cycle, la variation d’entropie
DS du gaz est nulle.
D) L’efficacité du moteur est −W / Q
2.
Travail récupéré sur l'énergie dépensée.
Toutes les affirmations sont justes.
22. Déterminer l’efficacité du moteur.
Premier principe sur le cycle
DU = 0 = W+Q
1+Q
2.
-W = Q
1+Q
2.
Rendement = -W / Q
2 = (Q
1+ Q
2 ) / Q
2.
Q
1+ Q
2 =nR (T
2 -T
1)ln a.
Q
2 =nR /(
g-1)(T
2-T
1)+nRT
2 ln a.
Rendement =(T
2 -T
1)ln a / [1 /(
g-1)(T
2-T
1)+T
2 ln a]=(
g-1)(T
2 -T
1)ln a / [(T
2-T
1)+(
g-1)T
2 ln a].
Rendement =(
g-1)(T
2 -T
1)ln a / [T
2(1+(
g-1) ln a -T
1].
Réponse
B.
23. . En considérant que ce moteur fonctionne entre les deux températures extrêmes T
f et T
c, quelle est l’efficacité du cycle
de Carnot correspondant ?
Variation d'entropie dans le cas du cycle de Carnot :
DS =0= Q
c / T
c +Q
f / T
f soit Q
f / Q
c = -T
f / T
c.
rendement = 1 +Q
1 / Q
2 = 1 +Q
f / Q
c =1-T
f / T
c.
Réponse
A.
24. Si on note S
c l’entropie créée au cours d’un cycle de ce moteur, quel est le bilan entropique du gaz au cours d’un tel
cycle ?
Q
c / T
c +Q
f / T
f + S
c =0 sur le cycle.
Réponse
B.