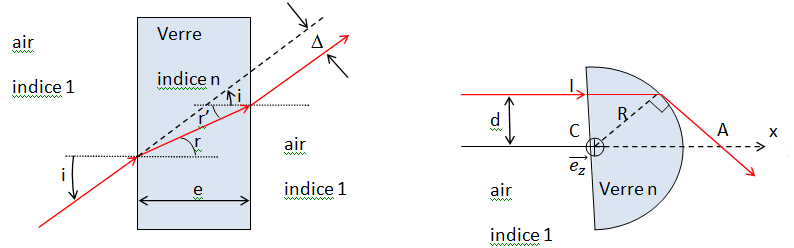
7. Un rayon lumineux atteint, sous un angle d’incidence i, l’un des dioptres d’une lame � faces parall�les en verre
d’�paisseur e et d’indice n. La lame est plong�e dans l’air (indice = 1). Apr�s travers�e de la lame, le rayon
�merge sous un angle
i'. Quelle est la relation entre i et i' ?
A) pas de relation particuli�re.
B) i' = -i.
C) sin i' = n sin i.
D) i' = i
.
Vrai.
R�fraction sur la face d'entr�e : sin i = n sin r.
Angle d'incidence sur la face de sortie : r' = r ( angles alternes internes ).
R�fraction sur la face de sortie : n sin r' = sin i'.
sin r' = sin r.
Par suite sin i = sin i' et i = i'.
8. Comment s’�crit, en fonction de e, n et i, l’�cart
D entre ce rayon �mergent et le prolongement du rayon incident ?
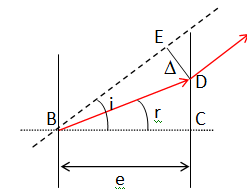
Triangle rectangle BCD : cos r = e / BD.
Triangle rectangle BED : sin(i- r )=
D / BD.
sin(i- r ) / cos r =
D / e ;
D = e sin(i- r ) / cos r.
Or sin (i-r) = sin i cos r -cos i sin r.
D = e(sin i -cos i tan r)= e cos i( tan i -tan r).
R�ponse
A.
9. Sur le second dioptre de la lame, le rayon est non seulement r�fract� comme pr�c�demment, mais il est aussi
partiellement r�fl�chi. Il retourne alors vers le premier dioptre o� il se r�fl�chit partiellement � nouveau et retourne
vers le second dioptre. Quelle est la dur�e
Dt de ce trajet (soit un aller-retour dans la lame) pour le rayon lumineux ?
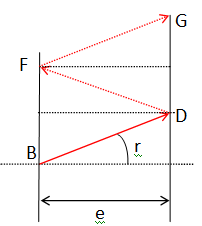
DF +FG = 2 BD = 2e / cos r.
C�l�rit� de la lumi�re dans la lame d'indice n : c / n.
Dt = 2e n / (c cos r ).
cos r = (1-sin
2 r)
� =(1-sin
2 i / n
2)
�.
Dt = 2e n / c (1-sin
2 i / n
2)
-�.
R�ponse
C.
10.
Le second dioptre est maintenant une surface h�mi-cylindrique.
L’ensemble
de ce dioptre et du dioptre plan pr�c�dent forme une lentille
h�mi-cylindre. Un rayon incident atteint le dioptre plan
en un point I, sous incidence normale, de sorte qu’il �merge du dioptre
cylindrique tangentiellement � ce dernier. Quelle doit-�tre la distance
d=CI pour obtenir cette configuration ?
A) d = nR.
B) d = R /n.
Vrai.
C) d = R.
D) d = n / R.
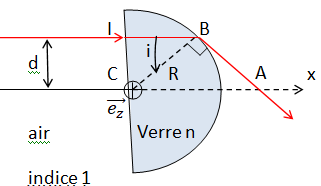
R�fraction en B : n sin i = 1 sin 90=1.
Triangle rectangle ICB : sin i = CI / R ;
Par suite CI =d= R / n.
11. En d�duire la distance AC qui s�pare du point d’intersection du rayon �mergent avec l’axe.
Triangle rectangle ABC : cos i = R / AC.
cos i = (1-sin
2 i)
� =(1-1/n
2)
� =(n
2-1)
� / n.
AC = R / cos i = R n / (n
2-1)
� .
R�ponse
B.
12. Un second rayon frappe normalement le dioptre plan de la lentille h�mi-cylindrique mais � une distance de C inf�rieure
� d. Par rapport au point A pr�c�dent, o� se trouvera le point d’intersection D avec l’axe du rayon �mergent de la
lentille h�mi-cylindrique ?
A) B est confondu avec A.
B) D est plus �loign� que A du centre de la lentille h�mi-cylindrique.
Vrai.
C) D est plus proche que A du centre de la lentille h�mi-cylindrique.
D) On ne peut rien dire a priori.
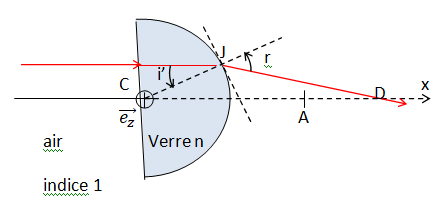
L'angle d'incidence i' est inf�rieur � i. Le rayon �mergent est donc moins d�vi�.
