Chute d'une goutte d'eau,  concours ENAC pilote 2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. . . .. .. ...... ... 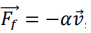Une gouttelette d’eau sph�rique, de masse m et de diam�tre D, tombe dans l’air en �tant soumise � trois forces de direction verticale : son poids, la pouss�e d’Archim�de F et une force de frottement visqueux due � l’air , o� v est lar vitesse de la gouttelette, dans le r�f�rentiel terrestre R suppos� galil�en, et a = 3 p h D, h �tant un param�tre caract�ristique de l’air appel� viscosit�. On pr�cise qu’il n’est pas n�cessaire de conna�tre cette grandeur pour r�soudre le probl�me pos�.  On donne la masse volumique de l’eau liquide, re ≈ 1000 kg. m-3, et celle de l’air, ra ≈ 1 kg. m-3 . 1. � l’aide d’une analyse dimensionnelle, d�terminer l’unit� SI (Syst�me International) de h. A) kg m s. B) kg m-1 s. C) kg m s-1  D) kg m-1 s-1. Vrai.  a s'exprime en N m-1 s soit en kg m s-2 m-1 s= kg s-1. a s'exprime en kg s-1 m-1. 2. On n�glige la pouss�e d’Archim�de devant les deux autres forces. Quelle est, sous forme vectorielle, l’�quation diff�rentielle du premier ordre qui d�crit le mouvement de la gouttelette dans R ? 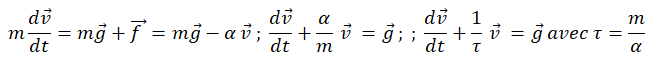R�ponse C.   3.  La pouss�e d’Archim�de �tant toujours n�glig�e, quelle est, dans R, l’expression de la vitesse sachant que la vitesse initiale de la gouttelette est nulle ? On choisit un axe vertical orient� vers le bas. L'origine est la position initiale de la goutte. Solution g�n�rale de l'�quation diff�rentielle sans second membre : v = A exp(-t / t) avec A une constante. Solution particuli�re de l'�quation avec second membre : v = vlimite = gt = mg / a. Solution g�n�rale de cette �quation : v = A exp(-t / t) + gt . A l'instant initial, la vitesse est nulle : 0=A+gt soit A = -gt. Par suite : v =gt (1-exp(-t / t)). R�ponse C.   4. On s’int�resse maintenant au vecteur position de la gouttelette. La pouss�e d’Archim�de �tant toujours n�glig�e, d�terminer r(𝑡) sachant que la position initiale de la gouttelette est nulle. Le vecteur position est une primitive du vecteur vitesse. r (t)=gt (t +t exp(-t / t))+ Cste. La position initiale est nulle : r (0)=gt (0 +t exp(-0 / t))+ Cste. 0 =g t2+ Cste ; Cste = -g t2 . r(t) = gt  t +g t2 exp(-t / t)-g t2 . r(t) = gt  t +g t2 (exp(-t / t)-1) R�ponse C.   5. Exprimer, en fonction de D, h, re et g, la vitesse limite vlim de la gouttelette, puis calculer sa valeur approximative. On donne D = 10 �m, h ≈ 2 � 10-5 SI (SI = Syst�me International des unit�s) et g ~ 10 m s-2. vlim = gt = mg / a avec m = 4 / 3 p (�D)3 re. a = 3 p h D. vlim = 4 / 3 p (�D)3 re g / (3 p h D). vlim =  D2 re g / (18  h ). vlim =10-10 x 103 x 10 / (36 10-5) = 0,1 /36 ~0,0028 m /s = 2,8 mm /s. R�ponse A. 6. On s’int�resse d�sormais � l’influence de la pouss�e d’Archim�de sur la valeur de vlim . Quel est l’�cart relatif , en pourcentage, entre la vitesse limite vlim A obtenue en tenant compte de la pouss�e d’Archim�de et la vitesse vlim obtenue pr�c�demment ? Volume de la goutte : V =4 / 3 p (�D)3. Pouss�e d'Archim�de : V ra g, verticale vers le haut. L'�quation diff�rentielle devient : dv/dt + v / t =g - V ra g / m =g - ra  / re g. vlim A = g(1-ra  / re ) t  ; vlim = gt ; |vlim A -vlim|=ra  / re g t. |vlim A -vlim| / vlim A= ra  / [ re(1-ra  / re )]. 1 / [1000 (1-10-3)]~0,001 ou 0,1 %. R�ponse B.

menu