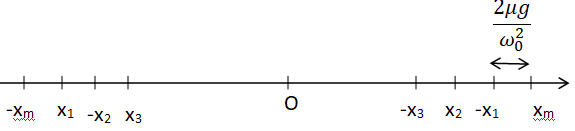Un
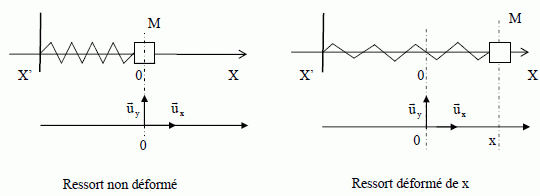
palet, assimilé à un point matériel M de masse m, est attaché à un
ressort (raideur k, masse négligeable) le long d’un
axe horizontal (Ox). On écarte, vers la droite (selon 𝑥 > 0), le
palet de la
distance
𝑥
m puis on le lâche sans vitesse initiale ; on observe
alors un
mouvement oscillatoire autour de la position d’équilibre prise,
par commodité, à la coordonnée 𝑥 = 0 lorsque le ressort n’est pas
déformé. Au cours du mouvement, le support (horizontal) sur lequel est
posé le palet exerce une force de frottement f=
eµmg
où g est la norme du champ de pesanteur, µ est un facteur
caractéristique du frottement et
e un nombre tel que :
e= −1
si le mouvement se fait dans le sens des 𝑥 croissants et
𝜀 = 1 sinon.
 31.
31. Quelle est
l’équation différentielle du deuxième ordre qui décrit le mouvement de
M ?
M est soumis à son poids, verticale, vers le haut, à l'action du
support, opposée au poids, à la tension du ressort T, horizontale, vers
la droite ( ressort étiré), norme k x, et à la force de frottement
solide.
Ecrire la seconde loi de Newton sur un axe horizontal :
-kx +f = mx" =md
2x /dt
2.
d
2x /dt
2 + k / m x =
eµg.
On pose
w02
= k / m ;
d
2x /dt
2 +
w02 x
=
eµg.
Réponse B.
32. Compte tenu
des conditions initiales, le mouvement de M s’effectue d’abord dans le
sens des 𝑥 décroissants. Quelle est
la solution x(t) de l’équation différentielle obtenue précédemment ?
Solution générale de l'équation sans second membre : x(t) = A cos (
w0t+
F) avec A une constante.
Solution particulière de l'équation complète :
x(t) =x =
eµg /
w02.
Solution générale de l'équation avec second membre :
x(t) = A cos (
w0t+
F)+
eµg /
w02.
Vitesse v = dx/dt = -A
w0
sin (
w0t+
F)
v(t=0) = 0 =A
w0
sin (
F) soit
F = 0.
x(t=0) = x
m =A
+
eµg /
w02
avec
e =1.
A = x
m -
µg
/
w02.
x(t) =( x
m -µg
/
w02)cos
(
w0t)+
µg /
w02.
Réponse B.
33. Cette première
phase du mouvement s’achève lorsque le mobile repart en sens inverse. À
quel instant t
1 cette première
phase du mouvement se termine-t-elle ? On exprimera t
1 en
fonction de la période T
0=2
p /
w0 du mouvement
oscillatoire.
A) t
1 = T
0.
B) t
1
= 2T
0.
C) t
1
=½ T
0 vrai
.
D) t
1 =
¼T
0.
v = dx/dt = -A
w0
sin (
w0t)
=( -x
mw0
+
µg /
w0) sin (
w0t).
v(t
1) = 0 =( -x
mw0 +
µg /
w0) sin (
w0t
1).
w0t
1
=(2k+1)
p.
k=0 ; t
1 =
p
/
w0
=½ T
0.
34. Quelle est la
position x
1 de M à l’instant t
1 ?
A) -xm. B) -x
m +2µg /
w02. Vrai. C) x
m -
2µg /
w02.
D) x
m +2µg /
w02.
x(t
1) =( x
m -µg /
w02)cos
(
p)+
µg /
w02.
x(t
1) = -x
m +µg /
w02+
µg /
w02=-x
m
+2µg /
w02.
35. À partir de
l’instant t
1
, choisi comme nouvelle origine temporelle, le mouvement de M
s’effectue dans le sens des x
croissants. Quel est l’instant t
2 pour lequel cette deuxième
phase du mouvement se termine ? Quelle est la position x
2 de
M à l’instant t
2 ?
A) t
2 = T
0.
B) t
2
= ½T
0.
Vrai.
C) x
2 =x
m +4
µg /
w02.
D) x
2 =x
m
-4
µg /
w02. Vrai.
x(t) = B cos (
w0t
)+
eµg /
w02.
x(t=0) = x
1 =B
+
eµg /
w02
avec
e =-1.
B = x
1 +µg /
w02=
-x
m +3µg
/
w02.
x(t) =( -x
m +3µg
/
w02)cos
(
w0t)-
µg /
w02.
v(t)= -
w0(
-x
m +3µg
/
w02)sin
(
w0t).
v(t
2)=0 ; t
2 =
p /
w0 =½ T
0.
x
2 =( -x
m +3µg
/
w02)cos
(
p)-
µg /
w02.
x
2 = x
m -3µg
/
w02-
µg /
w02= x
m
-4
µg /
w02.
36. . À partir de
l’instant t
2, le mouvement de M s’effectue de nouveau dans
le sens des x décroissants jusqu’à un instant t
3
où la position de M est x
3 et d’où le palet repartira dans
le sens des x croissants, et ainsi de suite. Compte tenu de ce qui
précède, quelle est l’expression générique de la durée t
n
(𝑛 entier naturel) de la n-ième phase du mouvement ? Donner
aussi l’expression générique de la position x
n atteinte à la
fin de la n-ième phase du mouvement.
A) t
n = n T
0
/ 2.
B) t
n = T
0
/ 2.
Vrai.
C) x
n =x
m
-n
µg /
w02.
D) x
n
=(-1)
n(x
m -2n
µg /
w02). Vrai.
Quelle que soit la phase considérée, elle dure ½T
0.
A chaque phase du mouvement, l'amplitude diminue de 2
µg /
w02.
|xn| = x
m -2n
µg /
w02 et x
n
=(-1)
n(x
m -2n
µg /
w02).