25. Quelles sont les affirmations
exactes ?
A) Le champ magn�tique �
l’int�rieur d’une bobine tr�s longue, de forme circulaire, est, loin
des bords, uniforme.
Vrai.
B) L’ordre de grandeur du
champ magn�tique terrestre est 50 mT. Faux ( ~50 �T)
C) Un moment magn�tique
est homog�ne au produit d’une surface par une intensit� �lectrique.
Vrai.
D) La norme
du vecteur moment magn�tique d’une spire circulaire (diam�tre D),
parcourue par un courant
d’intensit� I est
pID
2.
Faux (
pIR
2
)
.
26. Une spire
circulaire de diam�tre D est plac�e dans un champ magn�tique uniforme
de norme B. Quelle est la valeur
absolue maximale du flux
F
de ce champ � travers la spire ?
A) BS
vrai ;
B) B / S ;
C) S / B ;
D) nul.
Le flux est maximal lorsque le vecteur champ magn�tique et le vecteur
surface sont colin�aires et de m�me sens.
27. La norme du
champ magn�tique cr�� par une spire circulaire (diam�tre D), parcourue
par un courant stationnaire
d’intensit� I, s’�crit, � une distance z >> D sur l’axe de la
spire : B = �
0 I
a
D
� / (8z
3)
o� �
0 = 4
p10
-7
H. m
-1 et
a
et � sont deux exposants r�els. En utilisant l’analyse dimensionnelle,
trouver les valeurs de
a
et �.
A) a = 1 et � = 2.
Vrai.
B) a = 2 et � = 1.
C) a = 1 et � = 1.
D) a = 2 et � = 2.
Par analogie avec le champ magn�tique B =�
0 N / L I cr��
dans un sol�no�de :
a=1 ;
D
� / (8z
3) s'exprime en m
-1 ; �-3 = -1
soit � = 2.
28. La norme du
champ magn�tique pr�c�dent peut s’�crire en fonction de la norme
M du moment magn�tique de
la spire :
B = �
0 2
Mg / (4
p z
3).
En utilisant l’analyse dimensionnelle, d�terminer le facteur num�rique
g.
A) �. B) 1. Vrai. C) -1.
D) 2.
B s'exprime en tesla T ; �
0 s'exprime en T m
-1
; 1 /z
3 s'exprime en m
-3.
M
s'exprime en A m
2. Par suite
g = 1.
29. Dans le mod�le
plan�taire d’un atome d’hydrog�ne (mod�le de Bohr), l’�lectron (masse m
e
, charge �lectrique −e, o� e
est la charge �lectrique �l�mentaire) d�crit une orbite circulaire de
rayon r autour d’un axe de r�volution qui passe par
le proton p. L’axe de r�volution est orient� selon Oz. Le sens de
parcours de l’orbite est donn�. En
notant T la p�riode de r�volution de l’�lectron, ce syst�me est
assimilable � une spire circulaire parcourue par un courant
stationnaire d’intensit� I = −e / T.
Quelle est, d’une part, la composante
Mz , selon
𝑂𝑧, du moment magn�tique de ce syst�me et, d’autre part, la
composante L
z du moment cin�tique de l’�lectron par rapport
� son axe de r�volution ?
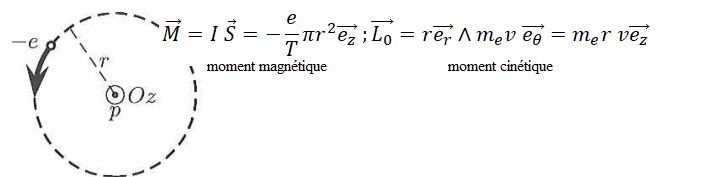
De plus v = 2
pr /
T ; L
z =2
p
r
2 m
e / T.
R�ponse
A.
30. .Le moment
cin�tique L
z est, en outre, un multiple entier de la
constante fondamentale
h
= h / (2
p) o� h
est la constante de
Planck : pr�cis�ment L
z = n
h o� n est un entier
sup�rieur ou �gal � 1. Quelle cons�quence cette quantification a-t-elle
sur
Mz ?
A) Il n’y a aucune
cons�quence particuli�re.
B) Le moment magn�tique
est alors quantifi� car
Mz
= −n e
h / (2m
e).
Vrai.
C) Le moment magn�tique
est alors quantifi� car
Mz
= n e
h / (2m
e).
D) On ne peut rien
dire a priori.
L
z =2
p r
2
m
e / T= n
h
.
Mz
= -e / T
pr
2
; 1 / T = -
Mz
/( e
pr
2
).
L
z = -2
m
e Mz
/( e ) = n
h .
Mz
= -e n
h / (2m
e).
