On s’int�resse ici � quelques consid�rations g�n�rales autour du moment cin�tique et de la rotation d’un corps rigide (ou
solide) autour d’un axe fixe dans un r�f�rentiel galil�en.
31. Que peut-on dire du vecteur moment cin�tique
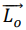
au point O d’un point mat�riel soumis � une force centrale de centre
de force O
?
A) Le vecteur
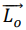
est une constante vectorielle.
Vrai.(
si seule cette force agit )
B) Seule la norme de
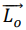
se conserve.
C) Seule la direction de
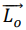
se conserve.
D) On ne peut rien dire a priori.
32. On consid�re un axe
D fixe dans un r�f�rentiel du laboratoire suppos� galil�en. Cet axe est orient� selon le vecteur
unitaire
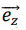
. Un solide est en rotation, avec la vitesse angulaire
(
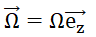
W > 0) autour de l’axe
D. Le moment d’inertie
du solide autour de cet axe est not� J. Quelle est la valeur du moment cin�tique L (
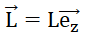
) de ce solide par rapport �
l’axe
D ?
A) L = -J
W.
B) L = J
W. Vrai.
C) L = -
W / J.
D) L = -�J
W.
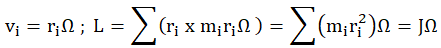33. . Quelles sont la ou les expressions correctes de l’�nergie cin�tique du solide au cours de sa rotation autour de l’axe Δ ?
A) �J
W2.
Vrai.
B) W2 / (2J).
C) L
2 / (2J).
Vrai.
D) -�J
W.
E
c = � J
W2.
Or L = J
W, donc E
c = L
2 / (2J).
34. Quelles sont les affirmations exactes ?
A) La liaison pivot ne permet pas une rotation autour d’un axe fixe.
Une liaison pivot ne permet qu'une rotation autour d'un axe d�termin�.
B) Une porte en rotation autour de l’axe form� par ses gonds est un exemple de liaison pivot.
Vrai.
C) En un point donn� d’une porte, et pour une force de norme d�termin�e, la m�thode permettant d’ouvrir la porte
le plus facilement consiste � appliquer la force perpendiculairement � la porte.
Vrai.
Moment de la force � appliquer � la porte : OM x F x sin (OM, F).
OM, distance de l'axe au point d'application de la foorce, doit �tre le plus grand possible.
De plus la force doit �tre perpendiculaire � la porte.
D) Si l’on exerce une force de norme donn�e, dont le vecteur correspondant est orthogonal � la porte, il sera
d’autant plus facile de fermer la porte que le point d’application de la force sera proche des gonds
35.
. On consid�re une porte, de largeur l = 80 cm, sur laquelle on exerce
une force orthogonale � la porte, de norme F=
120 N et dont le point d’application se situe � 80 cm de l’axe de
rotation. Quelle est la norme M du moment de cette
force ?
A) 96 N m
-1. ̇
B) 960 N m.̇
C) 96 N m.
Vrai.̇
D) 960 N m
-1.
M = l F = 0,8 x120 =96 N m.
fem induite : e
in = -d
F / dt = - B l x'.
36. On applique maintenant une force orthogonale � la porte, mais dont le point d’application est � 40 cm des gonds. Quelle
doit �tre la valeur F' de la force pour que le moment correspondant soit deux fois plus faible que le pr�c�dent ?
A) F' = 2F.
B) F' =�F.
C) F' = F.
Vrai.
D) F' = 3 F.
M' = F' x 0,40 = 48 ; F' = 48 / 0,40 =120 N.
