Une bo�te cubique d’arr�te a contient 𝑛 = 10
3
moles d’argon (masse molaire M=40 g. mol
-1). Dans ce probl�me, on note
𝑥, 𝑦 et 𝑧 les coordonn�es cart�siennes ; O est
l’origine du rep�re
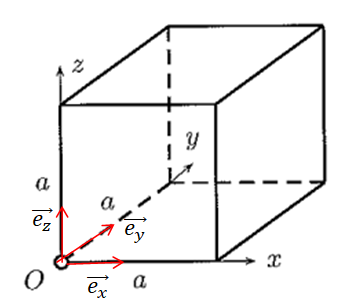13. Calculer le nombre N d’atomes dans la bo�te et la masse m d’un atome d’argon. On rappelle la valeur approximative de
la constante d’Avogadro 𝑁
A ≈ 6.10
23 mol
-1
.
A) 𝑁 ≈ 6.10
23 et 𝑚 ≈ 6,7.10
-23 kg.
B) 𝑁 ≈ 6.10
23 et 𝑚 ≈ 6,7.10
-26 kg.
C) 𝑁 ≈ 6.10
26 et 𝑚 ≈ 6,7.10
-23 kg.
D) 𝑁 ≈ 6.10
26 et 𝑚 ≈ 6,7.10
-26 kg.
Vrai.
m = 0,040 / (6 10
23) ~ 6,7.10
-26 kg.
N = 10
3 x 6 10
23 =6 10
26.
14. Un des atomes vient heurter la paroi en x=a, avec un vecteur vitesse
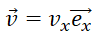
. La paroi �tant parfaitement rigide,
l’atome rebondit et repart dans la direction incidente avec le vecteur vitesse
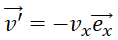
. D�terminer la variation du
vecteur quantit� de mouvement de l’atome.
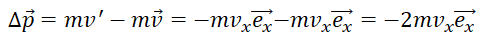
R�ponse
C.
15. On admet que l’atome poss�de un mouvement rectiligne et uniforme, le long de l’axe (𝑂𝑥), jusqu’� ce qu’il heurte de
nouveau la paroi. On admet aussi que lors d’une collision, l’atome, qui arrive avec un vecteur vitesse orthogonal � une
paroi, rebondit avec un vecteur vitesse oppos� au vecteur vitesse incident (avant le choc), sans changer sa norme.
Calculer la dur�e
t qui s�pare deux chocs successifs sur la paroi situ�e en x=a et en d�duire N
c
qui d�signe le nombre
de chocs par seconde de cet atome avec cette paroi.
A) t = 2a / v et N
c = 2 s
-1.
B) t = 2a / v et N
c = v / (2a).
Vrai.
C) t = a / v et N
c = v / a.
D) t = a / v et N
c = 1 s
-1.
L'atome parcourt la distance 2a � la vitesse v :
t = 2a / v.
N
c =1 /
t = v / (2a).
16. On admet que la paroi re�oit � chaque collision la quantit� de mouvement
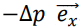
. Quelle est la force subie par la
paroi situ�e en x=a en raison des chocs r�p�t�s de l’atome ?
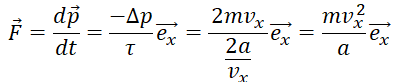
R�ponse
A.
17. En r�alit�, comme les atomes de la bo�te n’ont pas tous le m�me vecteur vitesse, on doit remplacer, dans l’expression
pr�c�dente, v
2x par v
2m
/ 3 o� v
2m
est la moyenne sur tous les atomes du carr� de la norme des vecteurs vitesse de chaque
atome. Donner la ou les expressions correctes de la pression P exerc�e par le gaz d’atomes sur la paroi situ�e en x=a ;
on note n
v
le nombre d’atomes par unit� de volume dans la bo�te.
Surface de la paroi S = a2 ; volume de la bo�te V = a3.
Pression = force / surface = N F / S = N m v
2m / (3a3).
nv = N / a3 ; P = nv m v
2m / 3 .
R�ponses
B et
C.
18. En admettant que le gaz dans la bo�te est un gaz parfait et que la pression ci-dessus est celle qui intervient dans la loi
des gaz parfaits, donner l’expression de la temp�rature 𝑇 de ce gaz.
T = PV / nR =
nv m v
2m a3/ (3nR).
nv a3 = N ; n= N / NA= nv a3 / NA.
T =mNA v
2m / (3R) = M v
2m / (3R).
R�ponse
A.
