Le satellite SMOS,  concours ENAC pilote 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités daptées à vos centres d’intérêts. . . .. .. ...... ... Le satellite SMOS est en mouvement circulaire autour de la Terre (masse M ≈ 6 × 1024 kg, rayon R~ 6 400 km) à une altitude h d’environ 700 km.  13. Quelles sont les affirmations fausses ? A) Le moment cinétique du satellite se conserve.  B) Le satellite est soumis à un champ de force centrale.  C) Le mouvement du satellite s’effectue dans un plan. D) Le mouvement du satellite s’effectue obligatoirement dans le plan équatorial. Inexact. L'interaction de gravitation, champ de force centrale, le moment cinétique se conserve. Le mouvement s'effectue dans un plan perpendiculaire  au moment cinétique. 14. Exprimer puis calculer la période de révolution T de SMOS. On donne la valeur approximative de la constante de Newton 𝐺 ≈ 7 × 10-11 N. m2. kg-2 . Troisième loi de Kepler : T2 / r3 = 4p2 / (GM) avec r = R +h= 6400+700 =7100 km =7,1 106 m. T = 2p [r3/ (GM)]0,5. T = 2 x3,14 [ (7,1 106)3/ (7 10-11 x6 1024 )]0,5 =5,8 103 s. Réponses A et D.   15. Exprimer la vitesse de satellisation v (vitesse sur une orbite circulaire) de SMOS.  A) GM / (R+h). B) [GM /(R+h)]½. Vrai. C) GM / h . D) (GM/h)½.. 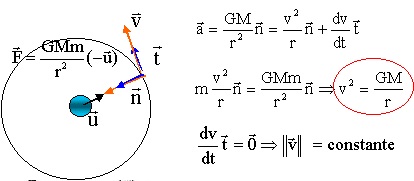16. Calculer v puis déterminer la vitesse de libération vl de SMOS. A)  v~7 km /s vrai ; B) v~7 km / h ;. C) vl=2 v. D) vl=2½ v. Vrai. v=[6 10-11 x 6 1024 / (7,1 106)]½ ~7 000 m /s = 7 km /s.. Vitesse de libértion : vitesse qu'il faut fournir pour envoyer le satellite à l'infini. Son énergie cinétique finale est nulle ; l'énergie potentielle est nulle à l'infini. Son énergie mécanique est nulle à l'infini. Ecinétique + Epotentielle = 0. Ecinétique = ½mvl2. Epotentielle = -GMm / r. ½mvl2=GM m / r . vl2=2GM  / r= 2 v2. vl=2½ v. 17.  Quelle serait l’altitude h de SMOS si son orbite était géostationnaire ? A) 3600 km ; B) 360 000 km ; C) 36 000 km vrai ; D) 42 000 km. T = 24 h = 24 x3600 =86400 s. Troisième loi de Kepler : T2 / r3 = 4p2 / (GM) r =[T2 GM /( 4p2 )]1/3 =[864002 x7 10-11 x6 1024 /( 4x3,142 )]1/3 =4,3 107 m=43 000 km. h = r-R = 43 000 -6400 ~36 000 km.   18. Par quelles relations l’énergie mécanique EM de SMOS est-elle reliée à son énergie cinétique Ec et à son énergie potentielle Ep ௣ A) EM=Ec=Ep ;  B) EM=Ec=½Ep ; C) EM= -Ec= ½Ep vrai ;  D) On ne peut rien dire a priori. Dans le cas d'un mouvement circulaire : Ec = ½mv2 ; v2 = GM / r ; Ec = ½ m G M / r. Ep = - GM m / r. EM = Ep + Ec = - GM m / r +½ m G M / r = -½ m G M / r = ½Ep.

menu