Exercice n�4 :
Le sommet de la tour Eiffel sert aussi au lancement
de feux d’artifice, notamment lors du 14 juillet.
On s’int�resse ici � la trajectoire des projectiles lanc�s du haut de
la tour Eiffel � une altitude h et avec une vitesse initiale 𝑉
0
comme indiqu� sur le sch�ma ci-dessous :
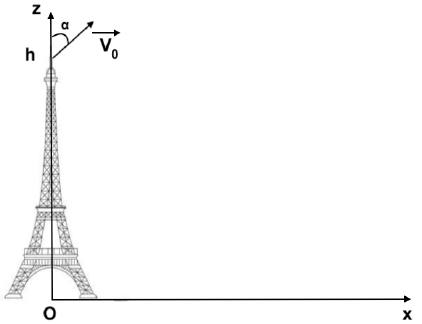
On utilisera le rep�re cart�sien (Oxyz) consid�r� comme galil�en pour
�tudier la trajectoire d’un projectile.
Le projectile se d�place uniquement dans le plan (Oxz). On n�gligera
toutes interactions avec l’air.
Donn�es : - Masse du projectile : m =200 g
- Intensit� du champ de pesanteur terrestre :g = 10 SI
- Sommet de la tour Eiffel : h=330 𝑚
- Vitesse initiale du projectile : V
0=20 𝑚 s
-1.
- Angle de tir :
a
=
p / 4.
22. L’unit� de
l’intensit� du champ de pesanteur terrestre est le :
A. N
B. kg m s
-1.
C.
kg m s-2.
D. m s
-2. Vrai
23.
Les coordonn�es de la position du projectile lors de sa chute sont :
A. x(t) = 10*2�t ;
y (t) =0 ; z(t) =-5t2 +10 *2�t+330.
Vrai.
B.
x(t) = 10*2�t ; y =-5t2 +10
*2�t ; z(t) = 0.
C.
x(t) =
0 ; y(t) =10*2�t ; z(t) =5t2 +10 *2�t+330.
D.
x(t) =
10*2�t ; y (t) = 330 ; z(t)=-5t2 +10 *2�t.
acc�l�ration : (0 ; -g) = (0 ; -10) ;
vitesse initiale : vx =vz = V0*2�
/ 2 = 10*2� ;
vitesse : vx = 10*2� ; vz = -10
t +10*2�
;
position initiale : (0 ; h = 330 m) ;
position x(t) =10*2� t ; z(t) =
-5t2
+10 *2�t+330. y(t) = 0.
24.
Le sommet de la trajectoire du projectile se situe � une altitude z de :
A. 330 𝑚
B. 340 𝑚. Vrai
C. 360 𝑚
D. 420 𝑚.
Au sommet la composante verticale de la vitesse est nulle :
vz = -10 t +10*2� =0 ; t = 2� ;
repport dans z(t) : -5 *2 +10 *2 +330 = 340 m.
25. L’�nergie m�canique du
projectile lors de sa chute est :
A. Em=700 J vrai
B. Em=40 J
C. Em=40 kJ
D. Em=700 kJ.
L'�nergie m�canique est constante, �gale � l'�nergie m�canique initiale.
Em = �mV
02 + mgh = 0,5 x 0,200 x20
2
+0,2 x10 x330 =40 +660 =700 J.
26. Afin de mieux
mod�liser la trajectoire, il faudrait prendre en compte une force de
frottement fluide f colin�aire et oppos�e � la vitesse. A t=0 , les
coordonn�es de f dans le rep�re (Oxyz) sont :
A. f
x = f *2
� / 2 ;
fy
= f *2� / 2 ; fz
= f *2� / 2 ;
B. fx = f *2� / 2 ;
fy
= 0 ; fz
= - f *2� / 2 ;
C. fx = -f *2� / 2 ;
fy
= f *2� / 2 ; fz = f *2� / 2 ;
D. fx =- f *2� / 2 ; fy =0 ; fz = -f *2�
/ 2 ; vrai.
La
tour Eiffel sert �galement � recueillir la temp�rature de l’air �
l’aide de capteurs. Un des capteurs d�tecte le flux thermique � travers
une paroi et en d�duit ainsi la temp�rature de l’air toutes les 10 ms .
Donn�es : - R�sistance
thermique de la paroi : Rth=5.10−4 SI
- Expression de la
r�sistance thermique : Rth=e / (lS)
- On note e l’�paisseur
de la paroi, S sa surface et l
sa conductivit� thermique
On �tudie le cas o� le
capteur d�tecte un flux constant de 1 kW sur une p�riode de 10 ms .
27. La r�sistance thermique
s’exprime en :
A. ohm
B. W .m−1
C.K.W −1
vrai
D. W m-1kg-1.
28. L’�nergie
�chang�e � travers la paroi pendant les 10 ms est de :
A. 1 J
B. 10 J vrai
C. 100 J
D. 1000 J.
�nergie (J) = puissance (W) fois dur�e (s) = 1000 x0,010 = 10 J.
29. La diff�rence
de temp�rature d�tect�e par le capteur entre les deux surfaces de la
paroi est alors de :
A. 5 �C
B. 2 �C
C. 0,5 �C vrai
D. 0,2 �C.
Dq =
flux thermique fois Rth =1000 x5 10-4 =0,5 �C.
30. En utilisant un
autre mat�riau pour la paroi dont la conductivit� est multipli�e par 2,
le flux d�tect� serait de :
A. 2 kW vrai
B. 10 kW
C. 5 kW
D. 1 kW.
La r�sistance thermique est divis�e par 2 ; pour un m�me �cart de
temp�rature, le flux thermique double.
