Particules chargées dans un champ électrique, Concours Avenir 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice n°1 : Afin d’analyser les molécules présentes dans l’atmosphère parisienne, un spectromètre de masse est installé au sommet de la tour Eiffel. Après capture des molécules atmosphériques, un laser pulvérise ces molécules en de nombreux fragments ionisés que l’on notera ici Mn+ (n représentant la charge du fragment). 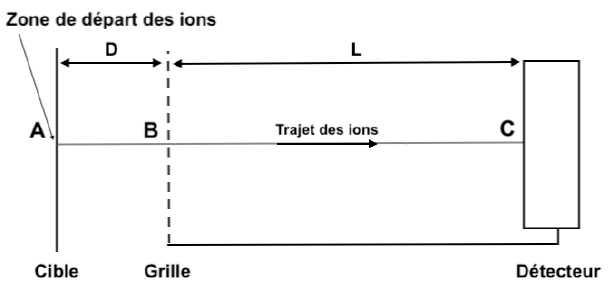Ces fragments sont ensuite placés dans une enceinte sous vide, pour d’abord être accélérés avant d’arriver sur un détecteur suivant le schéma suivant : Une tension UAB est appliquée entre les plaques A et B afin d’accélérer les fragments. Les fragments partent avec une vitesse nulle en A. Dans toute cette partie, le poids des fragments est négligeable. Entre B et C on considère qu’aucune force ne s’exerce sur les fragments. Aucun choc entre fragments n’a lieu entre A et C. On étudie le mouvement des fragments entre A et C, dans le référentiel terrestre supposé galiléen. Données : - Longueur d’onde du laser : l = 300 nm - Distance AB : D=40 mm - Distance BC : L=1200 mm - Tension appliquée entre A et B : UAB=20 kV - Charge d’un électron : e= -1,6 10-19 SI - Célérité de la lumière dans le vide : c = 300 000 km /s - La valeur du champ électrique régnant entre deux plaques conductrices en regard, soumises à une différence de potentiel U et distantes de d, s’exprime : E = U / d. 1. La fréquence des ondes utilisée par le Laser est : A. f= 1 1011 Hz B. f= 1 1012 Hz C. f= 1 1013 Hz D. f= 1 1015 Hz vrai f = c / l =3 108 / (300 10-9) =1 1015 Hz. 2. La charge d’un fragment M+ ionisé s’exprime en : A. Volt B. Faraday C. Coulomb vrai D. Electron-Volt. 3. La force appliquée entre A et B sur un fragment M+, de masse m=7 10-26 kg et pour lequel n=1 est : A. F=8.10−14 N vrai B. F=8.10−17 N C. F=8.10−20 N D. F=8.10−11N. E = UAB / D = 20 103 / 0,040=5 105 V / m. F = eE =1,6 10-19 x 5 105=8 10-14 N. 4. L'expression de la valeur de la vitesse en B d’un fragment M+ de masse m et pour lequel n=1 est : A. v= [2eUAB / m]½. Vrai B. v= [eUAB / (2m)]½. C. v= [2m /(eUAB)]½. D. v= [2e /(mUAB)]½. Théorème de l'énergie cinétique entre A et B : ½mv2-0 = e UAB ( travail moteur de la force électrique). v2=2e UAB / m. 5. Entre les points B et C, le mouvement des fragments dans le référentiel terrestre est : A. parabolique et uniforme B. parabolique et accéléré C. rectiligne et uniforme vrai D. rectiligne et accéléré. Entre B et C on considère qu’aucune force ne s’exerce sur les fragments.: le mouvement est donc rectiligne et uniforme ( principe d'inertie). 6. La durée de parcours entre les points A et C d’un fragment M+, de masse m et pour lequel n=1 est : A. t = D[m /(eU)]½ +L[m /(eU)]½ B.  t = D[2m /(eU)]½ +L[m /(2eU)]½. Vrai C.  t = L[m /(2eU)]½ D.  t = (L+D)[m /(eU)]½ . Mouvement uniformément accéléré entre A et B : a = eE / m = eU /(mD). AB =D= ½at2  = eU /(2mD) t2  ; t = D [2m /(eU)]½. Mouvement uniforme entre B et à la vitesse v = [2e U / m]½. Durée du parcours : L[m /(2e U )]½. Durée totale : D [2m /(eU)]½+L[m /(2e U )]½. 7. Plusieurs fragments partent de A en même temps. Les fragments qui arrivent les premiers sur le détecteur sont : A. les plus massiques parmi ceux qui ont une même charge B. les plus grands parmi ceux qui ont un même rapport masse / charge C. les plus petits parmi ceux qui ont un même rapport masse / charge D. les plus chargés parmi ceux qui ont une masse égale. Vrai. La durée du parcours AC est proportionnelle à (m / e)½.

menu