Physique, concours TSPEI 2020.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.
.. ..
......


...
Exercice 1. Imagerie optique par drone.
On souhaite utiliser un drone pour prendre des photos aériennes. Le système photographique embarqué consiste en un capteur électronique d'image (CMOS) de taille de pixel 10 µm et un objectif de focale 50 mm avec une ouverture maximale #f2. Le drone est en vol stationnaire à 50 m d'altitude.
1. A quelle distance se situe le capteur de la lentille ?
L'objet se trouvant à l'infini, l'image se forme dans le plan focal image de la lentille.
Le capteur est à 50 mm de la lentille.
2. A l'aide d'un schéma optique, calculer le grossissement optique du système d'acquisition d'images.

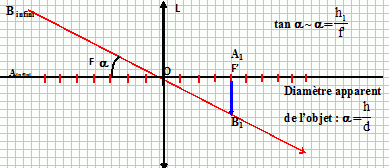Distance lentille objet : 50 m ; distance lentille capteur ( image) : 50 mm = 0,05 m.
Valeur absolue du grossissement : G =0,05 / 50 = 1,0 10-3.
3. Basé sur ce grossissement et la taille des pixels, calculer la résolution au sol des images obtenues.
10-5 / 10-3 = 10-2 m = 1 cm.
4. Vérifier que la résolution du système photographique ne sera pas limitée par la diffraction. On considère pour le calcul que l'image est monochromatique et prise à 550 nm.
La résolution au sol est très différente de la longueur d'onde ; la résolution  ne sera pas limitée par la diffraction.
5. Le capteur est un capteur CMOS couleur ( 8 bits par couleur primaire) de 1280 x1024 pixels.
On souhaite pouvoir observer en temps réel les images acquises grâce à une connexion Wifi (802.11g) permettant un débit de 25 Mbits /s. Ce taux de transfert est-il suffisant sachant que la caméra fonctionne à 60 Hz.
3 x 8 = 24 bits par pixel.
1280 x1024 x24 =3,15 107 bits= 31,5 Mbits.
Le débit de la connexion est insuffisant.
6. Quelle serait l'influence d'un filtre polarisateur sur la qualité de l'image ?
Le filtre influence les reflets et les couleurs des photos : parfait pour les prises de vue à l'extérieur.
Les filtres UV de grande qualité ont peu d'impact sur la qualité de l'image.
Exercice 2. Débitmètre électromagnétique.
Principe : le liquide traverse le débitmètre dans lequel un champ magnétique est appliqué. Le déplacement du liquide dans le champ induit une tension proportionnelle à la vitesse de déplacement. Cette tebsion est transmise à un amplificateur via 2 électrodes. La mesure de cette tension permet le calcul du débit.
1. Ce débitmètre peut-il fonctionner avec n'importe quel liquide ?
Non, le fluide doit avoir une conductivité électrique suffisante.
2. L'incertitude de mesure diminue avec la vitesse de déplacement. Elle est de 1 % à 0,2 m /s et tombe au dessous de 0,25 % pour 2 m /s. Sachant que le débit de l'installation varie entre 5 et 10 m3 / h, pourra-t-on toujours le mesurer avec une précision de 1% ?
Le diamètre d'entrée du capteur est égal à celui de la canalisation D = 50 mm.
Section S = pD2 / 4 =3,14 x0,052 /4 ~ 1,93 10-3 m2.
Débit : 5 / 3600 =1,39 10-3 m3 / s ; 10 / 3600 =2,78 10-3 m3 / s.
Vitesse =débit / S =  1,39 10-3 /(1,93 10-3) = 0,72 m /s.
2,78 10-3 /(1,93 10-3) = 1,44 m /s.
Ces valeurs sont comprises entre 0,2 m /s et 2 m /s. L'incertitude de mesure sera inférieure à 1 %.
 3. La tension induite U est liée à la distance L entre les deux électrodes, et à la vitesse v de déplacement du liquide par : U = B L v.
Calculer l'erreur relative sur le débit Q en fonction des paramètres et déterminer quel est le principal facteur influant sur la précision de la mesure ? Qu'en déduire sur le positionnement du capteur ?
Q = pD2 / 4 v ; v = 4 Q / (pD2).
 U est proportionnelle à la vitesse v : BL est considéré comme une constante.
U =4 BLQ / (pD2) ; Q = pD2 U  / (4 BL) = Cste D2 U.
DQ / Q = [(DD / D)2 +(DU / U)2]½.
U est le principal facteur influant sur la précision.
Le capteur de débit doit être monté de façon à ce que le tube de mesure soit constamment rempli. Préférer un montage dans une conduite ascendante en cas de montage à la verticale.

...
....

 Exercice 3. Courbe brachistochrone.
1. On considère une bille sur une pente inclinée AB. On note q l'angle OAB. La bille de masse m se déplace sans frottements le long de AB. Sa position sur l'axe AB est notée x ( A est pris comme origine). Ecrire l'équation du mouvement de la bille. En déduire le temps que mettra la bille à parcourir AB si sa vitesse à l'origine est nulle.

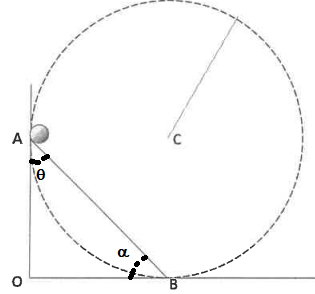
On pose a = p/2-q.
La bille est soumise à son poids, verticale vers bas, valeur mg et à l'action du plan, perpendiculaire au plan, vers le haut.
La seconde loi de Newton écrite sur l'axe AB donne : ma = mg sin q.
a = g sin a.
La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : v =g sin a t.
La distance parcourue est une primitive de la vitesse et la position initiale est l'origine.
x = ½g sin a t2.
t = [2AB /(g sin a)]½.
 2. On considère que la bille se déplace entre A et B sur une piste correspondant à un arc de cercle de centre C et de rayon R. Déterminer l'équation différentielle du mouvement.

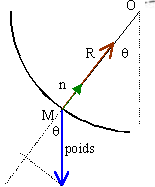
Ecrire la seconde loi de Newton sur un axe tangent à la trajectoire :
mgsin q = ma =m dv/dt.
dv / dt =g sin q .

3. Retrouver ce  résultat à partir du théorème du moment cinétique.
La dérivée du moment cinétique de la bille par rapport au point O fixe est égal au moment des forces extérieures appliquées au système.
Moment cinétique en O : L = R m v.
Le moment en O de l'action du plan est nul ; moment en O du poids : mg R sin q.
dL / dt = Rm dv/ dt = mg R sin q.
dv / dt =g sin q .
4. Montrer que dans les 2 cas, la bille atteint la même vitesse en B.
Théorème de l'énergie cinétique entre A et B.
½mv2B-0 = travail du poids.
Le travail de l'action du support, perpendiculaire à la vitesse est nul.
Travail moteur du poids en descente. Ce travail est indépendant du chemin suivi : mg AB sin a.

5. La courbe permettant de minimiser le temps de parcours AB n'est pas un arc de cercle. On se place dans un repère cartésienn xOY centré en O. Ecrire la longueur d'un élément infinitésimal de courbe dS en fonction de x et y. En déduire l'équation permettant de déterminer quelle sera la courbe minimisant le trajet.
ds =[ (dx)2+(dy)2]½= [1+y '2]½dx ave y' = dy / dx.
v = ds /dt = (2gy)½ d'après le théorème de l'énergie cinétique.
dt =[(1+y '2) / (2gy)]½dx
On intègre entre xA=0 et xB pour trouver le temps de parcours T et on cherche le minimum de T.
Formule de Beltrami : L-y ' dL / dy' = k, constante arbitraire.
L = [(1+y '2) / (2gy)]½  ; DL /dy' = y' / [(1+y '2) 2gy]½  ;
[(1+y '2) / (2gy)]½ - y'2 / [(1+y '2) 2gy]½  = k.
Multiplier chaque membre par [(1+y '2) 2gy]½  puis simplifier.
1 / [(1+y '2) 2gy]½  = k.
Equation cartésienne (1+y '2) y = cste.
Cste = altitude minimale atteinte par le point mobile.

Exercice IV. Energie nucléaire.
La réaction de fission de l'uranium 235 s'écrit :
23592U +10n --->14156Ba + 92wKr + y 10n.
1. Calculer w et y et énoncer les lois de conservation utilisées.
Conservation du nombre de nucléons : 235+1 = 141 +92 +y ; y = 3.
Conservation du nombre de la charge : 92 = 56 +w ; w = 36.
2. Calculer  en MeV l'énergie libérée par cette réaction.
Dm =m(14156Ba) + m(9236Kr)+ 2m(10n) -m(23592U) =140,914411+91,926156+2 x1,00866-235,0439299 = -0,1860 u
-0,1860 *1,66054 10-27 = -3,0893 10-28 kg
E = |Dm|c2 =3,0893 10-28 *9 1016 =2,78 10-11 J.
2,78 10-11 /(1,6 10-19)=1,78 108 eV = 174 MeV.
 3. Comparer l'énergie produite idéalement par 1 kg d'uranium au 42 MJ produits par la combustion de 1 kg de pétrole. Ce chiffre est-il réaliste ?
Dans 1 kg d'uranium il y a 1000 / 235 x6,02 1023 = 2,56 1024 atomes d'uranium.
Energie libérée : 2,56 1024 x2,78 10-11 =7,12 1013 J =7,12 107 MJ.
Soit 7,12 107 /42 =1,7 106 kg =1,7 103 tonnes de pétrole.
L'uranium naturel ne contient que 0,4 % d'uranium 235 fissile. On l'enrichit à 4 %. Cela conduit à 69 tonnes de pétrole.

4. La demi-vie de l'uranium 235 est d'environ 700 millions d'années. De combien sera  réduite une quantité d'uranium donnée après 2 dem-vie ? La demi-vie du thorium 232 est de 14,05 milliards d'années, lequel de ces deux éléments a la plus grande activité ?
A chaque demi-vie la quantité initiale est divisée par 2. Au bout de 2 demi-vie la quantité initiale sera divisée par 4.
Plus la demi-vie est grande, plus l'activité est faible.
Pour une mole : A =  Nl avec l t½ = ln 2 ; A = N ln 2 / t½ .

 5. Calculer l'activité en Bq / mol du thorium 232.
 t½  = 14,5 109 x365 x24 x3600 =4,57 1017 s.
A = 6,02 1023 xln2 /(4,57 1017 )=9,1 105 Bq / mol.
6. On trouve un fragment de tissu ancien dont on extrait  un échantillon de 14C. Son activité est 2 fois plus faible que celle d'un échantillon de 14C provenant d'un tissu fabriqué de nos jours. La demi-vie du carbone 14 est 5730 ans. En déduire l'âge du tissu.
A chaque demi-vie l'activité initiale est divisée par 2. Age du tissu : 5730 ans.



  
menu