Etude d'un congelateur, concours ing�nieur travaux publics ITPE 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. . . . . . . .. .. ...... ... L'ammoniac, nomm� aussi R717, est un fluide r�frig�rant qui trouve principalement une application dans le froid industriel, gr�ce notamment � sa grande efficacit� �nerg�tique. De nombreuses patinoires canadiennes utilisent l'ammoniac pour la fabrication de la glace. Pour obtenir une qualit� de glace optimale, la patinoire doit �tre r�frig�r�e. On fait ainsi circuler pr�s de 50 tonnes d'ammoniac dans une centaine de kilom�tres de canalisations pour assurer 10 cm de glace � −10�C sur l'ensemble de la piste. Pour la mod�lisation, on consid�re une masse m (NH3) = 1 kg d'ammoniac, dont la phase gazeuse est suppos�e parfaite. Le cycle est compos� de quatre �tapes :  A → B est une compression adiabatique r�versible : l'ammoniac, constitu� uniquement de vapeur, est comprim� de la pression de vapeur saturante PA = 2, 8 bar � la pression PB = 12 bar. Il passe de la temp�rature TA = −10�C � la temp�rature TB. B → D est une condensation isobare : le gaz est refroidi de mani�re isobare jusqu'� l'�tat B′ (vapeur saturante) puis se condense compl�tement, � la temp�rature TD = 30�C. La pression est maintenue constante : PB = PD. D → E est une d�tente adiabatique isenthalpique : l'ammoniac est d�tendu jusqu'� la pression PE = PA. On note x le titre massique en vapeur obtenu en E.  E → A est une vaporisation isobare : sous la piste, l'ammoniac liquide se vaporise totalement sous la pression PA. 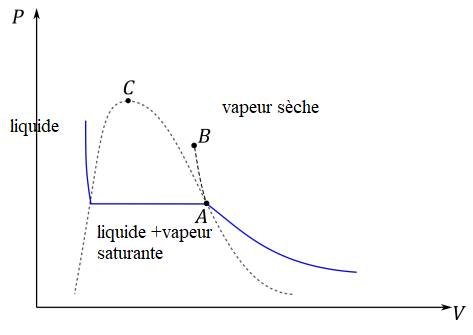Q.36 On donne dans le diagramme de Clapeyron o� figurent le volume V en abscisse et la pression P en ordonn�e, la position des points A et B ainsi que l'allure de l'isotherme � TA . Nommer la courbe en pointill�s. Pr�ciser l'�tat du fluide dans chaque zone. Justiffier l'allure de l'isotherme. Courbe en pointill�s : courbe de saturation. Dans les domaines diphas�s, les isothermes sont des droites. Dans les domaines monophas�s, les isothermes sont des branches d'hyperboles. Q.37 Reproduire la figure sur votre copie. Tracer l'isotherme �  TD. Placer les points B′ , D et E. Le cycle est-il moteur ou r�cepteur ? 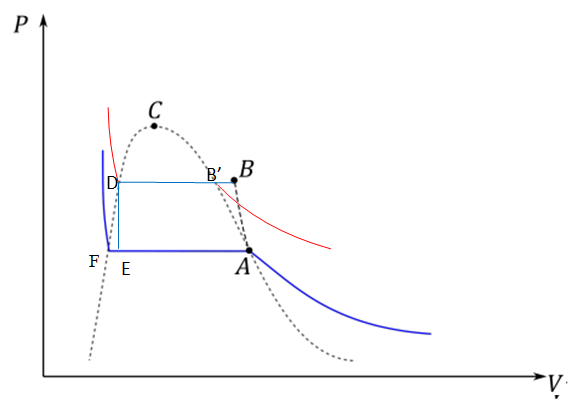Le cycle est parcouru dans le sens anti- horaire : cycle r�cepteur.  Q.38 Justiffier queTB > TA. D�terminer l'expression litt�rale de TB.   A → B est une compression adiabatique r�versible. Loi de Laplace : TAg PA1-g=TBg PB1-g . TB = TA (PB / PA)(g-1)/g=263(12 / 2,8)(1,3-1) / 1,3 ~368 K ( 95�C). pB > PA ; g-1 > 0 ; TB > TA. ... .... Dans la suite, on supposera que TB vaut 95�C. Q.39 Que valent les transferts thermiques QAB et QDE ?   A → B est une compression adiabatique r�versible : QAB =0. D → E est une d�tente adiabatique isenthalpique : QDE =0. Q.40 Exprimer le transfert thermique QBB′, entre les �tats B et B′ en fonction des donn�es.  Q.41 Exprimer le transfert thermique QB′D entre les �tats B′ et D en fonction des donn�es. En d�duire le transfert thermique QBD entre les �tats B et D. Faire l'application num�rique. La transformation �tant isobare, QBD est �gale � la variation de l'enthalpie massique c'est � dire : pour le fluide � l'�tat gazeux �voluant de TB � TB ' : QBB'=cp(TB '-TB) =2,1 (30-95)= -136,5 kJ kg-1. lors du changement d'�tat physique � temp�rature constante : -DHvap = -1,2 103 kJ kg-1. Cette valeur �tant n�gative, la chaleur est c�d�e au milieu ext�rieur. QBD = -136,5 -1,2 103 = -1,336 103 kJ Kg-1.   Q.42 Montrer que le titre massique en vapeur au point E s'�crit  x = cℓ (TD − TA) / DHvap (263 K) Faire l'application num�rique. x= FE / FA = cℓ (TD − TA) / DHvap (263 K) x = 4,7(30-(-10) / (1,3 103) =0,144.  Q.43 En d�duire le transfert thermique QEA lors de l'�vaporation sous la piste de la patinoire. Faire l'application num�rique. Pour 1 kg  : (1-0,144) x DHvap (263 K) =1,1128 103 kJ Kg-1. Pour 50 tonnes d'ammoniac : QEA = 50 103 x1,1128 103 = 42,8 103 x 1,3 103 =5,56 107 kJ. Q.44 D�terminer alors le travail total W fourni au fluide lors du cycle. Appliquer le premier principe � 1 kg du fluide sur un cycle : W+QAB +QBD + QDE +QEA=0. soit W= -QBD -QEA =1,336 103 -1,1128 103= 223 kJ kg-1.   Q.45 D�ffibir, en justiffiant soigneusement, l'efficacit� e de la machine frigoriffique puis l'exprimer en fonction de QEA et QBD. Faire l'application num�rique. efficacit� , rapport du gain sur l'�nergie d�pens�e = QEA / W= QEA /(-QBD -QEA)= -1/(QBD/QEA+1)=1,1128 103 / 223 ~5. Q.46 Montrer que l'efficacit� maximale emax d'une machine frigoriffique ditherme fonctionnant entre les temp�ratures TA et TD s'�crit : emax = TA / (TD-TA). Second principe de la thermodynamique : QEA / TA +QBD / TD = 0 sur le cycle. QBD / QEA =-TD / TA ; emax = 1/ ( TD / TA -1) = TA / (TD-TA). emax =263 / (30-(-10) ~ 6,6. Q.47 On d�ffinit le rendement r comme le rapport de l'efficacit� de la machine sur l'efficacit� maximale. Calculer le rendement de la machine. Commenter. r = 5 / 6,6 ~0,76, valeur assez �lev�e.

menu