Le drone
au service de l'agriculture, Concours général STL 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
En
survolant une exploitation agricole, le drone apporte de nombreuses
données pour l’agriculteur et lui permet d’adapter au mieux les apports
en arrosage, en engrais ou en produits phytosanitaires.
Étude simplifiée de la caméra
Le drone DJI Phantom 4 Multispectral embarque à l’aide d’une nacelle un
système composé de 6 caméras : une caméra RVB et cinq caméras
monochromatiques, dont une proche des infrarouges. Un logiciel de
traitement d’image permet ensuite la reconstitution de la cartographie
globale de l’exploitation agricole survolée.
La suite du sujet propose une étude simplifiée de ce système.
Données utiles :
- 6 capteurs CMOS
- 2,08 Mp x (1600 × 1300)
- Dimensions du capteur : 4,86 mm × 3,95 mm
- Distance focale f ’ = 5,74 mm
La caméra est située sous le drone qui se déplace à une altitude moyenne H = 180 m.
En optique, on modélise la caméra par :
- Un diaphragme
- Un objectif constitué d’une lentille mince convergente de distance focale f ’, fixe pour toute la durée du vol.
- Un capteur photosensible sur lequel se forme l’image de l’objet.
1. Préciser le rôle du diaphragme.
Il s'agit d'un élément mécanique placé sur le trajet de la lumière qui
conditionne la quantité de lumière transmise ainsi que l'ouverture du
système.
2. Justifier que l’on peut considérer que l’image de la parcelle se forme dans le plan focal image de l’objectif.
L'altitude du drone est h = 180 m. La distance lentille-objet est de
l'ordre de 180 m. La distance focale de la lentille est de quelques
millimètres. L'image d'un objet à l'infini se forme dans le plan focal
image de la lentille.
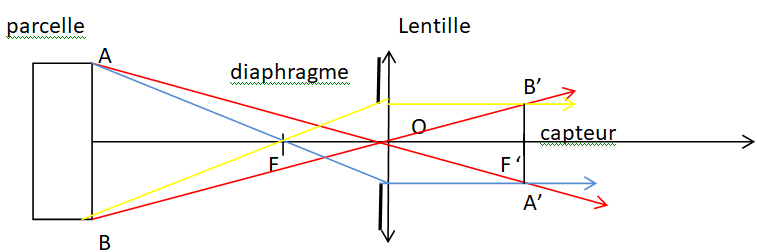
3. Faire un schéma,
sans souci d'échelle, faisant figurer la parcelle, le diaphragme, la
lentille convergente, le centre optique O et les foyers de la lentille
ainsi que le capteur CMOS.
Pour
avoir la meilleure image, il faut placer le diaphragme contre la
lentille ainsi elle est utilisée dans les conditions de Gauss.
4.
Déterminer les dimensions de la parcelle photographiée à l'altitude h =
180 m. L'image se forme sur toute la surface du capteur.
Valeur absolue du grandissement : f ' / H = 5,74 10-3/ 180 ~3,2 10-5.
Dimensions de la parcelle = dimensions du capteur / grandissement.
Dimensions du capteur : 4,86 mm × 3,95 mm.
Dimensions de la parcelle : 4,86 10-3 / (3,2 10-5 )~1,5 102 m ;
3,95 10-3 / (3,2 10-5 ) ~1,2 102 m.
5. Justifier la
formule de la "résolution au sol GSD " en supposant que GSD est la
taille d'un objet AB dont l'image A'B' se forme sur un pixel.
GSD = H / 18,9 cm / pixel avec H = altitude = 180 m.
GSD = 180 / 18,9 = 9,5 cm / pixel.
2,08 MP pour chaque capteur.
Surface d'un pixel : 3,95 x4,86 / (2,08 106)~9,2 10-6 mm2.
Dimension d'un pixel : racine carrée (9,2 10-6) ~3,04 10-3 mm.
Taille de l'objet se formant sur un pixel : 3,04 10-3 / (3,2 10-5) ~95 mm ou 9,5 cm / pixel.
6. La durée du vol
à vitesse maximale est d'environ 27 min et la fréquence maximale des
prises de vue est d'une image toutes les 4 s. Déterminer la surface
totale du champ qui peut être photographiée si les images sont mises
côté à côté sans recouvrement.
27 x 60 = 1620 s soit 1620 / 4 = 405 images.
Surface du champ : 1,5 102 x1,2 102 x405 ~7,3 106 m2 ou 7,3 km2.
7. Comparer à la surface de travail maximale donnée 0,63 km2 pour un taux de superposition latérale de 60 % et un taux de superposition avant de 80 %. Interpréter.
7,3 x(1-0,6) x (1-0,8) ~0,58 km2.
Ecart relatif : (0,63-0,58) / 0,63 ~0,08 (8 %).
Une utilisation d’engrais raisonnée.
La fertilisation azotée peut être maîtrisée et contrôlée à l’aide du survol des parcelles agricoles par les drones.
Étude du capteur RVB et de la photo obtenue.
Les images en couleurs du drone sont collectées grâce au capteur
RVB dans le domaine visible. La photographie ci-dessous est celle d’un
champ de betteraves prise par le drone.

1. Donner la signification de l’acronyme RVB.
Rouge, Vert, Bleu.
Les feuilles de betterave sont éclairées par la lumière blanche du soleil.
2. Préciser les couleurs absorbées et transmises par les feuilles de betteraves.
Le bleu est absorbé ; le rouge et le vert sont transmis.
3. Dans le codage RVB «
24 bits », chaque couleur primaire est codée sur un octet, soit 8 bits.
Déterminer le nombre de nuances de couleurs possible avec un codage «
24 bits ».
224=16 777 216 nuances.
4. Donner la signification du triplet (69 ; 38 ; 0).
Relier les valeurs numériques des deux triplets au caractère plutôt
clair ou plutôt foncé des pixels étudiés. Justifier. Conclure quant à
la possibilité de quantifier la quantité de végétation dans une zone
analysée grâce au caractère claire ou foncé du pixel.
Triplet (255 ; 255 ; 0) : teinte jaune très clair
Triplet (69 ; 38 ; 0) : teinte brun assez foncée, peu de végétation.
triplet (107 ; 109 ; 26) : teinte vert clair, quantité importante de végétation.
Exploitation du NDVI.
Les photos du drone dans le domaine du visible sont difficilement
exploitables pour définir la vigueur et la quantité de la végétation
d’une parcelle. Pour établir la carte de préconisation d’azote, le
logiciel calcule alors le NDVI (Normalized Difference Vegetation Index).
Sur la photo ci-dessous, à gauche une feuille de betterave sucrière ne
présentant aucune carence, tandis qu’à droite la feuille présente une
carence notable en azote.

1. Identifier le(s)
domaine(s) de travail des capteurs de la caméra mis en jeu dans la
réalisation de la carte de préconisation azotée.
R : réflectance des canaux rouge ; PIR : réflectance des canaux dans le proche infrarouge.
NDVI = (PIR-R) / (PIR + R).
2. À partir de ces
deux feuilles de betterave sucrière, établir un schéma récapitulatif
des rayons reçus et reflétés par les feuilles, suivant qu’elles
présentent ou non des carences.
En déduire si le NDVI sera supérieur ou inférieur pour la feuille carencée par rapport à la feuille en bon développement.
Lorsqu'une
plante est en bonne santé et en période de développement, elle pratique
la photosynthèse et la concentration en chlorophylle des feuilles est
importante. La plante absorbe toutes les couleurs et réfléchit
seulement le vert. Le NDVI se rapproche de 1.
En cas de carences ou lorsque la plante arrive à maturité , elle
absorbe toutes les couleurs sauf le jaune orangé. Le NDVI est faible,
proche de 0,1.
L'apport d'engrais.
L’engrais couramment utilisé par les agriculteurs est l’ammonitrate. Cet engrais permet de pallier le manque d’ions nitrate NO3-(aq) (aussi appelé azote nitrique) et d’ions ammonium NH4+(aq)
(azote ammoniacal) dans le sol. Cette partie aura pour objectif de
déterminer expérimentalement le pourcentage d’azote nitrique d’un
engrais azoté et le comparer aux indications de l'étiquette 16,7 % N
nitrique et 16,8 % N ammoniacal.
Mode opératoire du dosage des ions nitrate :
Préparation de la solution à titrer, réduction des ions nitrate NO3-(aq) :
On pèse à 0,01 g près m engrais = 1,20 g d’engrais. Après
avoir broyés les granulés à l’aide d’un mortier, on introduit la poudre
dans une fiole jaugée de 250 mL que l’on complète avec de l’eau
distillée. On obtient la solution S0.
On pèse avec précision m sel de Mohr= 7,85 g de sel de Mohr de formule Fe(NH4)2(SO4)2,6H2O
que l’on dissout ensuite dans une fiole jaugée de 100 mL en ajoutant de
l’eau distillée acidifiée par de l’acide sulfurique. On obtient la
solution S1 contenant des ions fer(II).
L’équation simplifiée de la réaction modélisant la dissolution du sel de Mohr dans l’eau est la suivante :
Fe(NH4)2(SO4)2,6H2O --> Fe2+(aq) + 2SO42−(aq) + 2NH4+ aq
Dans un erlenmeyer de 100 mL, on introduit :
- 20,0 mL de solution S0
- 20,0 mL de solution S1
- 10 mL d’acide sulfurique concentré
La transformation chimique étant lente, on porte à ébullition cette solution S pendant une quinzaine de minutes.
Titrage des ions fer(II) restant :
Une fois la solution S refroidie, on titre les ions Fe2+(aq) restants par une solution de permanganate de potassium KMnO4 à une concentration en quantité de matière de (5,00 ± 0,01)·10-2 mol·L-1. On procède à un premier titrage rapide puis à un deuxième titrage précis (à 0,05 mL près).
On obtient un volume équivalent VE de 11,95 mL.
Données : Masse molaire moléculaire du sel de Mohr : 392,13 g·mol-1.
1. Le titrage des ions nitrate dans l’engrais met en jeu deux réactions successives.
Nommer ce type de titrage et expliquer pourquoi on ne peut pas titrer directement les ions nitrate par les ions permanganate.
Titrage par différence :
Les ions nitrate de l'engrais réagissent de façon totale avec les ions fer (II) de la solution de sel de Mohr.
Les ions Fe(II) en excès sont ensuite titrés par une solution de permanganate de potassium.
Les ions nitrate sont des oxydants qui ne peuvent réagir qu'avec des réducteurs ( Fe2+ par exemple).
Étude de la réduction des ions nitrate NO3-(aq) :
2. Les couples d’oxydo-réduction mis en jeu lors de la transformation chimique prenant place dans l’erlenmeyer sont NO3-(aq) / NO(g) et Fe3+(aq) / Fe2+(aq). Écrire l’équation de la réaction modélisant la transformation chimique prenant place dans
l’erlenmeyer.
Réduction : NO3-(aq) +4H+aq + 3e- --> NO(g) +2H2O(l).
Oxydation : 3 fois { Fe2+(aq) --> Fe3+(aq)+ e- }.
Ajouter et simplifier : NO3-(aq) +4H+aq +3 Fe2+(aq)--> NO(g) +2H2O(l) + 3 Fe3+(aq).
3. Déterminer la quantité de matière d’ions Fe2+ dans la solution S1, puis la quantité de matière d’ions Fe2+ initiale dans la solution S, notée n Fe2+ initial.
m sel de Mohr/ M( sel de Mohr) = 7,85 /392,13 = 0,020 mol dans 100 mL de S1.
n Fe2+ initial =0,020 x20 / 100 =4,0 10-3 mol.
La transformation modélisée par la réaction entre les ions nitrate et les ions Fe2+ étant totale, établir la relation entre la quantité de matière d’ions Fe2+ initiale, la quantité de matière d’ions Fe2+ restante n Fe2+ restante et la quantité de matière d’ions nitrate n nitrate réellement contenue dans la solution S.
n Fe2+ restante= n Fe2+ initial - 3 n nitrate.
Dosage des ions fer (II) restant :
4. Écrire l’équation de la réaction support du titrage des ions fer (II) Fe2+ par les ions permanganate MnO4-.
Le couple d’oxydo-réduction du permanganate étant MnO4–(aq)/Mn2+(aq).
Oxydation : 5 fois { Fe2+(aq) --> Fe3+(aq)+ e- }.
Réduction : MnO4–(aq)+ 8H+aq + 5 e- --> Mn2+(aq) +4H2O(l).
MnO4–(aq)+ 8H+aq +5 Fe2+(aq) --> Mn2+(aq) +4H2O(l)+5Fe3+(aq).
5. Décrire le changement de couleur observé au moment de l’équivalence.
MnO4–(aq) couleur violette ; les autres ions sont icolores ou faiblement coloré.
Avant l'équivalence, MnO4–(aq) est en excès, la solution est violette.
Après l'équivalence, MnO4–(aq) est en défaut, la solution est pratiquement incolore.
En exploitant la relation à l’équivalence entre les quantités de matière nMnO4- et n Fe2+ restante
, montrer que la quantité de matière d’ions nitrate dans la prise
d’essai s’exprime au final par la relation suivante et calculer sa
valeur :
nNO3-=(n Fe2+ initial - 5 nMnO4-) / 3.
A l'équivalence : n Fe2+ restante = 5 nMnO4-.
n Fe2+ restante= n Fe2+ initial - 3 n nitrate.
5 nMnO4- = n Fe2+ initial - 3 n nitrate.
3 n nitrate = -5 nMnO4- + n Fe2+ initial .
n nitrate = (-5 nMnO4- + n Fe2+ initial) / 3.
nMnO4- = 5,00 10-2 x VE = 5,00 10-2 x 11,95 10-3=5,975 10-4 mol.
n nitrate =( 4 10-3 -5 x 5,975 10-4 ) / 3 = 3,375 10-4 mol dans 20 mL de S0.
Soit 4,22 10-3 mol dans 250 mL ( dans 1,20 g d'engrais).
6. En déduire le pourcentage massique d’ions nitrate dans les 1,2 g d’engrais. Conclure.
M(nitrate) = 14 +3 x16 = 62 g / mol.
m(nitrate) = 62 x 4,22 10-3 ~0,26 g.
0,26 / 1,2 x100 ~21,7 %.
Ecart relatif avec l'indiication de l'étiquette : (21,7 -16,7) / 16,7 ~0,30 (30 %).
|
...
|
....
|
Le mouvement du drone.
Le
mouvement du drone Le drone DJI Phantom 4 Pro possède quatre moteurs
identiques et une masse totale m = 1 487 g. L’accélération de pesanteur
est égale à g = 9,81 m·s-2. Le mouvement du drone est étudié dans le référentiel terrestre supposé galiléen.
Décollage du drone.
Lors de l’ascension, le drone s’élève verticalement avec une vitesse ascensionnelle constante va = 6,0 m·s-1 jusqu’à une altitude h= 180 m.
1. Déterminer la valeur du poids P du drone.
P = m g = 1,487 x 9,81 ~14,6N.
2. Déterminer la
valeur minimale de la force ascensionnelle verticale F délivrée par
chaque moteur afin que le drone puisse s’élever jusqu’à l’altitude
souhaitée.
La valeur minimale de F doit être égale à la valeur du poids, soit pour chaque moteur : 14,6 / 4 ~3,65N.
3. Déterminer la durée de la phase ascensionnelle.
h / va =180 / 6,0 = 30 s.
Autonomie de la batterie.
4. Donner la signification de l’acronyme LiPo.
Lithium-Polymère.
5. Déterminer l’énergie maximale disponible dans la batterie de vol quand celle-ci est entièrement chargée.
Capacité : 5 870 mAh ; tension : 15,2 V.
5,870 Ah soit 5,870 x3600 = 21 132 coulombs.
Energie maximale : 15,2 x 21 132 = 3,21 105 J.
La notice du drone précise que la collecte des données photographiques
se fait « pendant un vol qui vide la batterie de 100% à 30% ».
6. Estimer la durée du vol si les quatre moteurs sont utilisés à puissance maximale 35 W par moteur.
Energie utilisée : 3,21 105 x 0,70 = 2,25 105 J.
Durée du vol : 2,25 105 / (4 x35) =1,6 103 s ou environ 27 minutes. ( en accord avec les données).
7. Déterminer le temps nécessaire à la recharge complète de la batterie.
Chargeur : tension 17,4 V ; puissance 100 V.
énergie utilisée / puissance du chargeur = 2,25 105 / 100 = 2,25 103 s ou environ 38 min.
Chute contrôlée du drone.
Dans le référentiel terrestre supposé galiléen, on modélise le drone
par une sphère de diamètre égale à 40 cm, de masse m et on étudie le
mouvement de son centre de masse O pendant la chute.
Lorsque la batterie est quasiment déchargée, le drone se met en mode
stationnaire : sa vitesse dans le référentiel terrestre est nulle. Il
réduit alors la puissance de ses moteurs afin de réaliser une chute
verticale contrôlée pour revenir au sol.
On considère que les forces qui influent sur son mouvement, en plus de
son poids, sont la force ascensionnelle verticale des 4 moteurs ayant
pour valeur F = 13 N et les frottements dans l’air modélisés par une
force f de valeur proportionnelle à la vitesse f = 0,7 v et de sens contraire à la vitesse.
1. Donner une raison pouvant expliquer l’intérêt que peut avoir le drone à réduire la puissance de ses moteurs.
Pour descendre, la force verticale ascendante des moteurs doit être inférieure au poids.
2. Représenter, sans souci d’échelle, les forces qui s’exercent sur le drone.
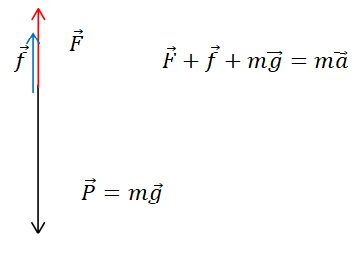
3. En utilisant la
deuxième loi de Newton montrer que l’équation différentielle modélisant
la vitesse du drone au cours de sa chute peut s’écrire sous la forme : t dv / dt + v = V où la vitesse est exprimée en m.s-1 et le temps en s.
4. Exprimer V et t en fonction de k, m, g et F.
Ecrire la seconde loi de Newton selon un axe vertical orienté vers le bas :
-F -k v +mg = m dv / dt.
m / k dv / dt + v = (mg - F) / k.
On pose t = m / k et V = (mg - F) / k.
5. Expliquer ce que
devient cette équation différentielle en régime permanent, et
déterminer la valeur de la vitesse atteinte par le drone en régime
permanent. Conclure.
En régime permanent dv / dt = 0.
vlimite = V =(mg- F) / k =(1,487 x 9,81 -13) / (7,0 10-1) = 2,7 m /s..
6. Identifier et déterminer la valeur du temps caractéristique.
t = m / k =1,487 / (7,0 10-1) =2,1 s.
La vitesse limite de chute est atteinte au bout de 5t soit environ 10 s.
|
|