Mathématiques,
QCM,
Concours ESA 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Exercice 1. 6 points.
Une seule bonne réponse ; une bonne réponse rapporte 1 pt, une réponse fausse -0,25 pt et l'absence de réponse 0 pt.,
QCM 1. Une suite est telle que pour tout entier naturel n : 1 < u n+1 < u n. Alors :
A. La limite de u n est égale à 1 si n tend vers plus l'infini.
B. La limite de un est égale à 0 si n tend vers plus l'infini.
C. La suite converge. Vrai.
D. La suite diverge.
1-un < un+1-un < un-un.
1-un < un+1-un < 0 : la suite est décroissante ; la suite est minorée par 1 : donc elle converge. .
QCM 2. La suite (v n) est définie pour tout entier naturel par : v n = 5-1 /(n 2+1) est :
A. Décroissante sur N.
B. Croissante sur N. Vrai.
C. Non monotone sur N.
D. Minorée par 5 sur N.
v0 = 4 ; v1 = 4,5 ; v2 = 5-1 /5 = 4,8 ; v3 =4,9; vn =5 si n tend vers plus l'infini.
vn+1-vn =5-1 /((n+1)2+1) -5+1 /(n2+1) =1 /(n2+1) - 1 /((n+1)2+1).
vn+1-vn =[(n+1)2+1- (n2+1)] / [((n+1)2+1)(n2+1)].
Le dénominateur est positif.
Le numérateur vaut : (n+1)2-n2 =(2n+1) positif.
vn+1-vn >0, la suite est croissante sur R.
QCM 3.
La suite (Sn) est définie pour tout entier n non nul par Sn = 1 +1 /4 +...+1 / 4n. Alors la suite :
A. a pour limite 2.
B. a pour limite 4,/3. Vrai.
C. n'a pas de limite.
D. a pour limite +oo.
Sn est la somme des termes d'une suite géométrique de raison 1 /4 et de premier terme 1.
Sn = (1-0,25n)/ / (1-0,25 ) ; 0,25n tend vers 0 si n tend vers plus l'infini.
Sn tend vers 1 / 0,75 = 4 / 3.
QCM 4.
Soit la fonction f définie sur ]0 ; +oo[ par f(x) = ln((x+1) / x) -1 /(x+1). La dérivée de f(x) a pour expression :
A. x /(x+1) -1/(x+1)2.
B. -1 /(x(x+1)).
C. -1/(x(x+1)) +1 /(x+1)2.
D. -1 /(x(x+1)2). Vrai.
Dérivée de (x+1) / x en posant u = x+1 ; v = x : u' = 1 ; v' = 1 ; (u'v-v'u) / v2 =(x-(x+1)) / x2 = -1/x2.
Dérivée de ln((x+1) / x) : [-1 /(x2)] / [(x+1) / x] = -1 / [x(x+1)].
Dérivée de -1 /(x+1) : 1 /(x+1)2.
Dérivée de f : -1 / [x(x+1)] + 1 /(x+1)2 = [-(x+1) +x] / [x(x+1)2] = -1 / [x(x+1)2].
QCM 5.
Soit E =exp(1+ln(2)) / (3 exp(1+ln(3)). Alors E est égale à :
A. 0,25
B. (e+2) /(e+9).
C. 2 / 9. Vrai.
D. 1 /3.
exp(1+ln(2) / exp(1+ln(3)) =exp(1+ln(2) x exp(-1-ln(3) =exp(1+ln(2)-1-ln(3)) =exp(ln(2)-ln(3)) exp(ln(2 /3)) =2 /3.
E = 2 /(3 x3) = 2 /9.
QCM 6.
On considère la fonction g définie sur R par g(x) =cos2(x) -2 cos(x). La dérivée de g(x) a pour expression :
A. sin2(x) +2 sin(x).
B. -2 cos(x) sin(x) +2 sin(x). Vrai.
C. 2 sin(x)(cos(x)-1)
D. 2 sin2(x) -2 sin(x).
Dérivée de cos2(x) : -2 sin(x) cos(x) = -sin(2x).
Dérivée de -2 cos(x) : 2 sin(x).
Dérivée de g : -2 cos(x) sin(x) +2 sin(x).
Exercice 2. 6 points.
QCM 7.
La fonction h définie sur R par h(x) =xe2x a pour primitive :
A. H(x) = x2e2x /4.
On dérive en posant u = x2 ; v = e2x ; u' = 2x ; v' = 2e2x.
u'v + v'u = 2xe2x+2x2e2x.
B. H(x) = (2x+1)e2x.
On dérive en posant u = 2x+1 ; v = e2x ; u' = 2 ; v' = 2e2x.
u'v + v'u = 2e2x+2(2x+1)e2x.
C. H(x) = 0,5 xe2x.
On dérive en posant u = 0,5x ; v = e2x ; u' = 0,5 ; v' = 2e2x.
u'v + v'u = 0,5e2x+xe2x.
D. H(x) =(0,5x-0,25)e2x. Vrai.
On dérive en posant u = 0,5x-0,25 ; v = e2x ; u' = 0,5 ; v' = 2e2x.
u'v + v'u = 0,5e2x+(x-0,5)e2x = xe2x.
QCM 8.
L'intégrale suivante est égale à :
A. e3+1.
B. e3+4.
C. e3-7. Vrai.
D. e3-1.
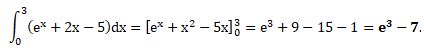
QCM 9.
Le plan ayant un vecteur normal de coordonnées (-1 ; 3 ; 2) et passant par le point A (-1 ; 0 ; 0) a pour équation cartésienne :
A. -x-3y+2z-5 =0.
B. -x+3y+2z+2=0.
C. x-3y-2z+1=0. Vrai.
D. x+3y-2z+1=0.
Equation de ce plan : -x+3y+2z+d=0
A appartient à ce plan : 1 +0 +0 +d = 0 soit d = -1.
Par suite : -x+3y+2z-1 = 0 ou bien x-3y-2z+1=0.
QCM 10.
La
couverture vaccinale contre la diphtérie-tétanos est de 90 % chez les
jeunes de 15 ans. On interroge au hasard 50 jeunes de 15 ans à propos
de cette vaccination. On assimile ce sondage à un tirage avec remise.
Soit X la variable aléatoire dénombrant les jeunes de 15 ans vaccinés
contre la diphtérie-tétanos parmi les 50 jeunes interrogés.
A. P(X = 0) = 50 10-49.
B. En moyenne 45 jeunes parmi les 50 sont vaccinés. Vrai.
C. P(X = 50)~ 1.
D. X suit une loi binomiale de paramètre n = 15 et p = 0,9.
n = 50 ; p = 0,9 ; expérance E(X) = n p = 50 x0,9 = 45.
P(X=0) = (500) x 0,90 x 0,150 = 0,150 .
P(X=50) = (5050) x 0,950 x 0,10 = 0,0051.
.
QCM 11.
Soit la fonction f définie sur ]0 : +oo[ par f(x) = ln(x) / ln(10), alors :
A. Pour tout x de ]0 ; +oo[, f(x) = x / 10
B. Pour tout entier naturel n non nul, f(3n) = 3 f(n).
f(3n) = ln(3n) / ln(10) =ln(3) / ln(10) +ln(x) / ln(10).
3f(n) = 3 ln(n) / ln(10).
C. f(1 / 3) = 1-f(3).
f(1/3) = ln(1 /3) / ln(10) = -ln(3) / ln(10).
f(3) = ln(3) / ln(10) ; 1-f(3) =1-ln(3) / ln(10).
D. Pour tout x réel de ]0 ; +oo[, f(3x) = f(3) + f(x). Vrai.
f(3x) = ln(3x) / ln(10) =ln(3) / ln(10) +ln(x) / ln(10).
f(3) = ln(3) / ln(10).
QCM 12.
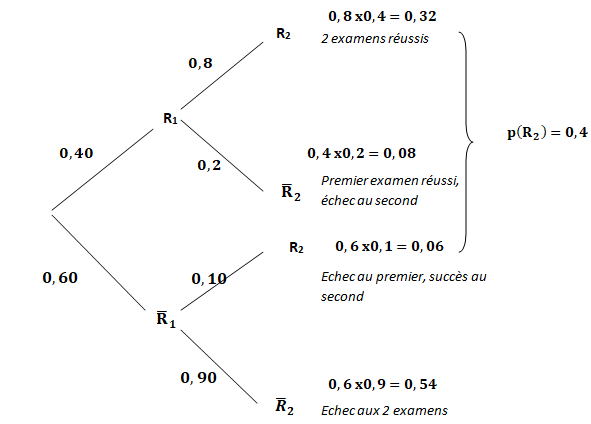
Pour
se préparer aux partiels, les étudiants en première année passent deux
examens blancs, 40 % d'entre eux réussissent le premier examen. La
probabilité d'échoué au second est 0,9 si l'étudiant a échoué au
premier et 0,2 si le premier est réussi.
A. La probabilité qu'un étudiant réussisse les 2 examens est strictement supérieure à 0,4.
B. La probabilité qu'un étudiant réussisse le deuxième examen est strictement supérieure à 0,74.
C.
Si un étudiant réussit le deuxième examen blanc, la probabilité qu'il
ait également réussi le premier est strictement supérieure à 0,4. Vrai.
P(R1 n R2) / P(R2)=0,32 / 0,4 = 0,80.
D. Si un étudiant échoue au deuxième examen, la probabilité qu'il ait échoué au premier est strictement inférieure à 0,75.
P(non R1 n non R2) / P(non R2)=0,54 / (0,54 +0,08) = 0,87.
|
...
|
....
|
Exercice 3 (8 points).
ln(2) ~0,7 ; ln(0,0005) ~-7,6 ; racine carrée (0,0736)~0,27.
Un patient consulte un oncologue.
Partie A. Test.
L'oncologue réalise un test pour savoiur si la tummeur est opérable ou non. Pour cela, il mesure le temps t0 ( heure) mis pour que la quantité q d'une substance S0 injectée dans l'organe malade atteigne son maximum.
Puis il applique la règle de décision suivante :
si t0 < 20 la tumeur est opérable sinon elle n'est pas opérable.
On note q(t) la quantité, exprimée en mg de la substance S0 dans l'organe malade à l'instant t ( heure). q est solution de l'équation différentielle (E) :
2y'+y= -0,001t +3,998.
y est une fonction définie et dérivable sur [0 ; 100].
1.a. Résoudre l'équation E0 : 2y'+y = 0.
y' +0,5y = 0 ; y = A e-0,5t avec A une constante.
b. Déterminer les réels a et b tels que la fonction g(t) = at +b soit une solution particulière de (E).
g' = a, repport dans (E) :
2a +at+b = -0,001t +3,998.
On identifie : a = -0,001 ; 2a+b = 3,998 ; b = 4.
g(t) = -0,001t + 4.
c. En déduire les solutions de (E).
q(t) = A e-0,5 t -0,001t +4.
2.a. Démontrer que la solution q de (E) qui vérifie q(0) = 0 est q(t) = 4-0,001t -4 e-0,5t.
q(0) = A +4 = 0 ; A = -4.
b. Calculer q'
q'(t) = -0,001 +2e-0,5t.
c. Etudier les variations de q.
q'(t) = 0 si e-0,5t = 0,001 /2 = 0,0005 soit t = -ln(0,0005) / 0,5 ~7,6 / 0,5 ~15,2.
si t < 15,2, q'(t) >0 et q(t) est croisante.
si t > 15,2, q'(t) < 0 et q(t) est décroisante.
d. Donner la valeur de t0 pour laquelle q est maximale. Quelle est la décision de l'oncologue ?
t0 ~15,2 h : la tumeur est opérable.
Partie B. Récidive.
Après l'opération, l'oncologue effectue un prélèvement sur les tissus
voisins de la tumeur enlevée, qu'il envoie à un laboratoire d'analyse.
Ce laboratoire injecte dans le prélèvement une substance S1 composée de 1000 cellules de type A.
On note N(t) le nombre de cellules de type A à l'instant t, exprimée en jours. N(t) = 1000 ert.
Il applique la règle de décision suivante :
si le temps mis, pour avoir 2000 cellules de type A dans le
prélèvement, exède 10 jours, on dira que le risque de récidive est
élevé, sinon il est modéré.
Le laboratoire annonce que le nombre de cellules de type A a quadruplé au bout de 28 jours.
1. Donner la valeur exacte de r.
4000 = 1000 e28r ; 4 = e28r ; ln(4) = 28 r ; r = ln(4) / 28.
2. Quel est le risque de récidive pour ce patient ?
2000 = 1000 exp[ln(4) / 28 t] ; 2 = exp[ln(4) / 28 t] ; ln2 = ln(4) / 28 t = 2 ln(2) / 28 t ;
1 = t / 14 ; t = 14 jours.
Le risque de récidive est
élevé.
Partie C . Chimiothérapie.
Le traitement est effectué en intraveineuse. La concentration du
médicament ( µmol / L) peut être modélisée par c(t) = D / K (1-exp(-Kt
/ 80)).
D réel positif représentant le débit d'écoulement du médicament dans la perfusion, exprimé en micromole par heure.
K, réel positif représente la clairance( capacité du patient à éliminer
plus ou moins vite le médicament ) du patient, exprimé en litre par
heure.
1. Détermination de la clairance.
On règle de débit de la perfusion à 120 µmol / h ; au bout de 6 heures;
on prélève un échantillon de sang et on mesure la concentration du
médicament qui est égale à 4,5 µmol / L.
a. Justifier que la clairance K est solution de l'équation : 120(1-exp[ -3 K / 40] -4,5 K = 0.
4,5 = 120 / K (1-exp(-6K
/ 80).
4,5 K =120(1-exp(-3K / 40 ) ; 120(1-exp[ -3 x / 40] -4,5 x = 0.
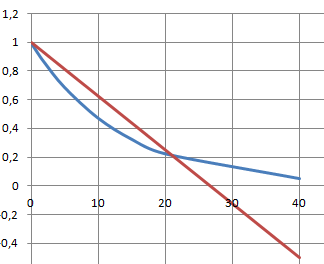
b. Montrer que cette équation admet une solution unique sur ]0 ; +oo[.
1-exp[ -3 x / 40] =4,5 / 120 x.
exp[ -3 x / 40] =1-4,5 / 120 x.
sur ]0 ; +oo[ : exp[ -3 x / 40] décroît de 1 à 0 ;
1-4,5 / 120 x décroît de 1 à -oo.
On prendra K = 21 pour la suite du problème.
2. Réglage du débit.
a. Déterminer la limite l de la fonction c en +oo en fonction du débit D.
c(t) = D / K (1-exp(-Kt
/ 80)).
En +oo, le terme en exponentielle tend vers zéro.
La limite de c(t) est égale à D / K = D / 21.
b. La concentration
du médicament dans le sang se rapproche rapidement de sa limite. Cette
concentration limite doit être égale à 10 µmol / L. En déduire la
valeur du débit à régler par le médecin.
10 = D / 21 ; D = 210 µmol / h.
.
|
|