Sciences
physiques,
Concours EMIA, école militaire interarmes 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
L'orage.
I. Eclair et tonnerre.
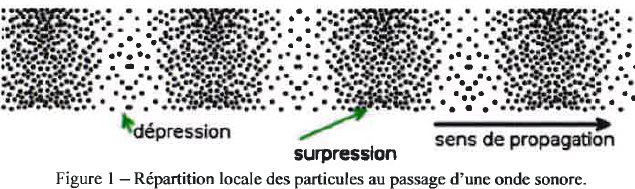
1. L'onde sonore
est-elle transversale ou longitudinale ? Justifier.
Onde longitudinale : l'onde se propage dans la même direction que la
variation de pression, succession de dépression et surpression.
2. Calculer les
longueurs d'onde correspondant à 20 Hz et 20 kHz, limites des
fréquences audibles par l'homme.
cson = 340 m / s à 20°C.
lmin
= cson / fmax =340 / 20 000
=0,017 m.
lmax = cson
/ fmin =340 / 20 =17 m.
3. Indiquer si les
affirmations suivantes sont vraies ou fausses en justifiant.
Affirmation 1
: une onde quelconque se propage toujours dans un milieu matériel.
Faux, une onde électromagnétique peut se propager dans le vide.
Affirmation 2
: une onde sonore peut se propager dans le vide.
Une onde mécanique ( onde sonore par exemple ) nécessite un milieu de
propagation.
Lors d'un orage, la foudre tombe à 3,4 km d'un promeneur. L'éclair et
le tonnerre sont émis simultanément au moment où la foudre tombe.
4. Au bout de
combien de temps le promeneur verra t-il l'éclair ? Au bout de combien
de temps entendra-t-il le tonnerre ?
Eclair : t = 3,4 103 / (3,0 108)~1,1 10-5
s.
Tonnerre : t = 3400 / 340 =10 s.
5. Justifier la
technique qui consiste à compter les secondes entre l'éclair et le
tonnerre et à les diviser par 3 pour obtenir la distance en km à
laquelle la foudre est tombée.
Secondes comptées / 3 = distance (m) / ( 3 x 340) =distance ( km
) / (3 x0,34) ~ distance (km) / 1,02 ~ distance ( km)
II. Etude du
condensateur Terre-Ionosphère.
On
considère que la terre et son atmosphère constituent les deux
armatures d'un volumineux condensateur sphérique. La terre de rayon R
est chargée
négativement -Q, l'ionosphère, représentée par une surface
équipotentielle de rayon R+h, porte une charge positive +Q. On suppose
que l'atmosphère située entre les deux a la permitivité du vide e0.
1. Faire un schéma
de la situation en plaçant un point M quelconque situé à la distance r
du centre de la terre, telle que R < r < R+h. Représenter le
repère sphérique au point M.

2. Justifier que le
champ électrostatique en M ne dépend que de la variable r.
Dans une distribution sphérique, il y a invariance par rotations autour
du point O, centre de la sphère. En M le champ électrostatique, ne
dépend pas des coordonnées q
et j. Le champ électrostatique en M ne dépend
que de la variable r.
3.
Citer des plans de symétrie et d'antisymétrie de la distribution de
charges passant par le point M. En déduire la direction du champ
électrostatique en M.
Tout plan contenant le point M et le centre O de la sphère est plan de
symétrie de la distribution de charge. Donc le champ électrique en M
appartient à tous ces plans, c'est à dire à la droite OM. Le champ
électrique est selon cette droite, donc radial.
4. Appliquer le
théorème de Gauss et montrer que 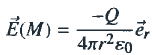
On considère comme surface de Gauss une sphère de centre O et de
rayon r = OM. Le champ étant constant sur cette surface et orthogonal à
la sphère, le flux du champ à travers cette surface est simplement le
champ multiplié par la surface :
F = 4 p r2 E(r)= -Q / e0.
5. Rappeler le lien
entre le champ électrique et le potentiel V. Donner alors l'expression
du potentiel V(r) puis celle de la différence de potentiel entre la
terre et l'ionosphère DV
= V(R+h) - V(R).
E = -dV / dr ; V(r) = Q /(4pe0r)
+ V0, avec V0 une contante d'intégration.
V(R) = Q /(4pe0R)
+ V0,
V(R+h)=Q /(4pe0(R+h)) + V0,
DV =Q /(4pe0)
[1 /(R+h) - 1 / R]= -h Q / [4pe0(R+h)R].
6. En déduire la capacité C du
condensateur terrestre définie par C = Q / DV en fonction de R, h et e0.
C = 4pe0(R+h)R
/ (-h)
7. Lors de l'émission d'un éclair,
la tension est de l'ordre de 100 millions de volts. Calculer la charge
Q. e0
= 8,85 10-12 F m-1. R = 6371 km et h = 80 km.
R+h =6451 km = 6,451 106 m. R =
6,371 106 m.
Q = C U =
4 x3,14 x8,85 10-12 x 6,451 106 x6,371 106
/( -8,0 104) x 108= -5,71 106 C.
Averse.
On étudie la chute d'une goutte d'eau, modélisée par une sphère de
rayon a, de masse m, composée d'eau de masse volumique r = 1,0 103 kg m-3
et tombant dans l'air de masse volumique rair = 1,2 kg m-3.
La goutte est soumise à une force de frottement fluide f = 6phav où v est sa vitesse et
h = 2,0 10-5 Pa s est la viscosité de l'air.
1. Justifier
que l'on peut négliger la poussée d'Archimède devant son poids.
V : volume de la goutte.
Poids P = V r g ;
poussée F = Vrair
g.
P / F = r / rair=1,0
103 / 1,2 ~800.
2. En utilisant la
seconde loi de Newton, établir l'équation différentielle vérifiée par
la vitesse de la goutte.
L'axe Oz est dirigé vers le bas.
La goutte est soumise à son poids et à la force de frottement,
verticale, vers le haut.
mg -6phav = m dv/ dt.
dv / dt +6pha
/ m v = g.
On pose t = m / (6pha).
dv / dt +v / t =
g. (E).
3. Résoudre cette équation sachant
que la vitesse initiale est nulle.
Solution générale de dv / dt +v / t =0 : v = A exp(-t / t) avec A une constante.
Solution particulière de (E) : vlim = g t.
Solution générale de (E) : v = A exp(-t / t) + g t.
La vitesse initiale étant nulle : 0 = A+ g t ; A = -g t.
v = g t ( 1- exp(-t / t)).
4.
Montrer que vlim = 2a2rg/(9h).
vlim
= g t=
gm (6pha) ; m = 4 / 3 p a3r.
vlim = 2a2rg/(9h).
A.N : a = 2,00 mm = 2,00 10-3 m.
vlim =2 x4,00
10-6x 103 x9,81 /(9 x2,0 10-5)=4,36 102
m /s.
a = 0,10 mm = 1,0 10-4
m.
vlim
=2 x1,00 10-8x 103 x9,81 /(9 x2,0 10-5)=1,1
m /s.
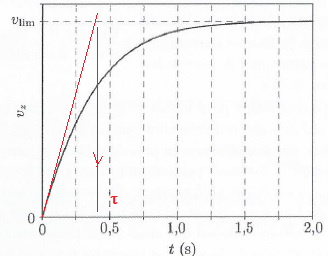
5. Dessiner l'allure du graphe de
v(t) en indiquant t
et vlim.
La forme ronde d'une goutte est due à son énergie de surface Es
= g S où g = 70 mN m-1
est la tension superficielle de l'eau et S la surface de la goutte.
Lorsque la goutte s'écrase, elle dissipe la totalité dr son énergie
cinétique Ec. Cela peut avoir pour effet de la faire
exploser si son énergie de surface est inférieure à son énergie
cinétique.
6. Rappeler
la formule de l'énergie cinétique.
Ec = ½m v2.
7. En
comparant les valeurs de Ec et Es de la goutte,
déterminer l'expression de la valeur limite du rayon de la goutte pour
qu'elle ne se fragmente pas en s'écrasant.
Fragmentation si Es
< Ec.
g 4pa2 < ½mv2.
m = 4 / 3 pa3 r.
g <
ra / 6
; a >6 g / r.
a > 6 x70 / 1000 ; a > 0,42 mm.
8. Les gouttes de la question 4
vont-elles se fragmenter ?
La grosse goutte se fragmente ; la petite goutte ne se fragmente pas.
|
...
|
....
|
IV. Réactions
nucléaires dans les nuages.
Des isotopes radioactifs 137 N et 158O
naissent au coeur des nuages d'orages.
1. Donner la
composition d'un noyau d'azote 14.
7 protons et 14-7 = 7 neutrons.
2 et 3.
Quelle particule est émise lors de la réaction de transformation d'un
noyau d'azote 14 en azote 13 sous l'effet d'un rayonnement g ? Ecrire
l'équation correspondante.
147 N
+ 00 g --> 137
N +10 X (
neutron).
4. La particule
émise a une énergie de E0 = 10 MeV. Convertir cette valeur
en joule.
10 x 106 x1,6 10-19 =1,6 10-13 J.
5. L'azote 13 décroît rapidement par
radioactivité ß+. Quel est le type de particule émise ?
Transformation d'un proton en neutron : positon 01e.
11p --> 10n
+01e.
6. En déduire la composition et la
nature du noyau fils.
137 N
--> 01e
+ 136 C.
7. Le temps de
demi-vie de l'azote 13 vaut 598 s. Que signifie cette valeur ?
Au bout de 598 s, la moitié des noyaux d'azote 13 se sont désintégrés
en carbone 13.
V. Protection des circuits
électriques contre la foudre.
Fusible simple.
Son
nom vient du fait qu'il y a fusion d'un filament conducteur sous
l'effet de son élévation de température provoquée par la surintensité.
Les premiers fusibles étaient en plomb.
r =
11,35 103 kg m-3 ; Tf = 327 °C ; c =
129 J K-1 kg-1 ; g = 4,81 106 S m-1.

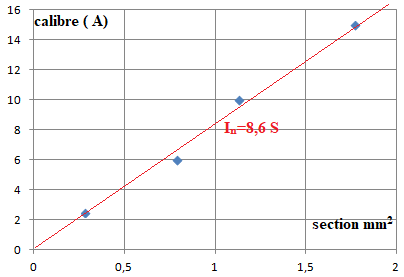
1. Tracer sur un
graphe le calibre In des 4 fils en fonction de leur
section S. Que remarque t-on ?
Calibre
In(A)
|
2,5
|
6
|
10
|
15
|
Diamètre
d (mm)
|
0,6
|
1
|
1,2
|
1,5
|
Section
S =pd2
/ 4 mm2
|
0,282
|
0,785
|
1,13
|
1,77
|
In
/ S
|
8,86
|
7,64
|
8,85
|
8,47
|
3. Quelle est la
puissane P dissipée par effet Joule dans le fusible de résistance R
traversé par l'intensité I ?
P = RI2.
L'énergie électrique reçue par le fusible le chauffe pendant la durée Dt depuis la température T0
= 20 °C jusqu'à sa température de fusion.
PDt = mc (Tf-T0).
Résistance du fil de longueur L de section S : R = L /(gS).
4. Exprimer la
masse m en fonction de sa masse volumique, de sa section et de sa
longueur.
m = r L S.
5. Montrer que I
est proportionnelle à S.
RI2Dt = mc (Tf-T0)
; L /(gS) I2Dt = r L S.c (Tf-T0)
.
I2Dt = r S2.c (Tf-T0)g .
I2 = r S2.c (Tf-T0)g / Dt.
I = a S avec a = ( r c (Tf-T0)g / Dt)½=(11,35
103x129 x317 x4,81 106 / Dt)½=4,72
107/ Dt½.
6. En
comparant l'expression de a obtenue à la question 5 à la valeur donnée
à la question 2, en déduire le temps caractéristique du fusible Dt.
8,6 A / mm2 =8,6 106 A / m2.
8,6 106 = 4,72 107/ Dt½.
Dt½
=47,2 / 8,6 ~5,48 ; Dt ~30
s.
Fusible composé.
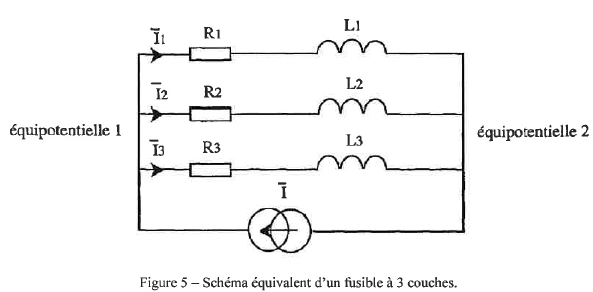
On note U la tension aux bornes des trois branches.
1. Donner la
relation liant les courants I, I1, I2 et I3.
Loi des noeuds : I = I1 + I2
+ I3.
2. Dessiner le
circuit équivalent à très basse fréquence ( courant quasi-continu ). A
quelle condition a t-on I1=I2=I3.
Les inductances se comportent comme des interrupteurs fermés ( petit
fil conducteur ).
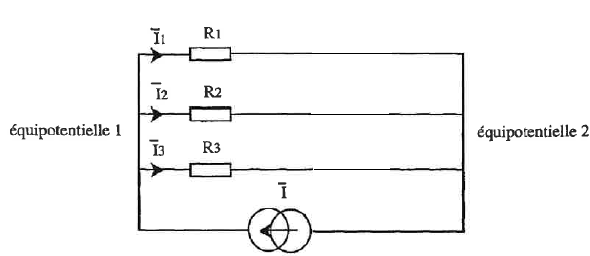
Si R1=R2=R3 alors I1=I2=I3.
On se place maintenant en régime sinusoïdal forcé de pulsation w.
3. Déterminer les
imédances Zi
des différentes branches.
Zi = R + jLi
w.
4. Donner
l'expression des courants complexes Ii traversant
les différentes branches.
Ii = U / Zi .
5. A haute
fréquence, quel est l'effet domminant ? Quel terme peut-on négliger
dans les expressions de Zi
?
L'effet domminant est
du à l'inductance Li. Le terme R devient négligeable devant
le terme Lw.
6. Quel est alors
le déphasage entre le courant et la tension ? Lequel est en avance sur
l'autre ?
La tension est en avance de ½p
sur l'intensité.
|
|