Mathématiques, concours recrutement professeur des écoles 2022

Exercice 4.
Soit M un nombre entier naturel inférieur à 100. On note u le chiffre des unités du nombre M et d son chiffre des dizaines.
Soit N un nombre entier naturel inférieur à 100, ayant le même chiffre d des dizaines que M et tel que son chiffre v des unités vérifie u+v=10.
Par exemple, pour M = 34, alors N = 36 vérifie ces conditions.
Pour M et N vérifiant les conditions ci-dessus, on propose d’utiliser l’algorithme ci-dessous pour calculer le produit M×N.
Algorithme de calcul.
- On calcule le produit de d et de l’entier suivant d+1.
- On calcule le produit de u et de v.
- On ajoute au produit de u et de v, 100 fois le produit de d et de l’entier suivant d+1.

1. Vérifier en détaillant les calculs que cet algorithme fonctionne pour 34×36.
d = 3 ; d+1 = 4 ; d x (d+1) = 3 x4 = 12.
100 d x (d+1) = 1200.
u x v = 4 x 6 = 24.
1200 +24 = 1224 ; 34 x 36 = 1224.
2. Démontrer que cet algorithme de calcul donne effectivement le résultat escompté pour tous les couples de nombres M et N vérifiant les conditions mentionnées en début d’exercice. On pourra utiliser les égalités M=10d+u et N=10d+v.
P=(10 d + u) ( 10 d + v) =100d² +10 d x v + 10d x u + u x v.
P =100d² +10 d (u+v) +u x v.
u+v = 10.
P =100d² +100 d +u x v.
P = 100 d x (d+1)+ u x v.

3. Montrer comment on peut utiliser cet algorithme de calcul, en détaillant les calculs, pour calculer mentalement 4,2×4,8.
M = 42 avec d = 4 et u = 2.
N = 48 avec d = 4 et v = 8.
M x N / 100 = d x (d+1)+ u x v / 100.
M x N /100 = 4 x 5 + 2 x 8 / 100 =20 +0,16 = 20,16.
4,2 x 4,8 = 4 x 5 +0,2 x 0,8.

Exercice 5.
On propose un jeu dans une cour de récréation.
Pour cela on s’appuie sur des croix peintes au sol comme indiquée sur le schéma ci-dessous :

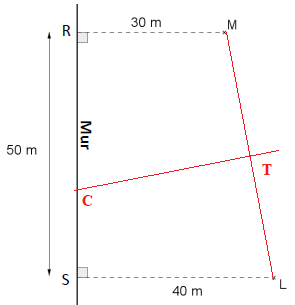
- la croix M est située à 30 m du mur d’enceinte de l’école (MR = 30 m) ;
- la croix L est située à 40 m du mur d’enceinte de l’école (LS = 40 m) ;
- les points R et S sont distants de 50 m (RS = 50 m).
Mila, une élève, se trouve sur la croix M et Lucien, un autre élève, se trouve sur la croix L. L’enseignante souhaite que Mila et Lucien courent tous les deux vers un même point de contact au mur ; le gagnant sera le premier à toucher ce point sur le mur. Pour que l’épreuve soit équitable, l’enseignante souhaite que le point de contact soit à égale distance des positions initiales des deux élèves, c’est-à-dire des croix L et M.
1. Construire à l’échelle le plan de la cour avec les points M, L, R et S en choisissant comme échelle 1 cm pour 5 m.
2. a. Sur la figure, construire le point T, milieu du segment [ML]. Tracer la droite perpendiculaire à (ML) et passant par T. On note C le point d’intersection de cette droite avec le mur.
b. Justifier que le point C est le point de contact cherché.
C appartient à la médiatrice du segment [ML]. Donc [MC] = [LC].
c. Mesurer la longueur RC sur le plan et en déduire une estimation de la distance entre les points R et C dans la cour de récréation.

3. On note x la distance, exprimée en mètre, entre les points R et C dans la cour de récréation.
a. Déterminer les longueurs MC et CL en fonction de x.
Le triangle RMC est rectangle en R.
Relation de Phytagore : MC² = RM² + RC².
MC² = 30² + x².
MC = (900 +x²)^½.
Le triangle LSC est rectangle en S.
Relation de Phytagore : LC² = SL² + SC².
LC² = 40² + (50-x)².
LC² =1600+2500+x²-100x.
LC² =4100+x²-100x.
LC = (4100 +x²-100x)^½.
b. En déduire la distance entre les points R et C dans la cour de récréation.
40² + (50-x)² = 30² + x².
40²-30² =x²-(50-x)² .
700 =(x+50-x) (x-50+x).
700 = 50 (2x-50).
14 = 2x -50.
64 = 2x soit x = 32.