A. Vitesse et cadence d'un cycliste lors
d'un entraînement.
Dans un sport d'endurance, comme le cyclisme, les principaux
indicateurs de la performance
sont la consommation maximale d'oxygène utilisée lors d'un effort
intense, caractérisée par la
capacité V
O2max, et la puissance maximale dite « aérobie »,
notée P
MA. La capacité V
O2max
est une limite: elle correspond au volume maximum de dioxygène consommé
par unité de
temps et par unité de masse corporelle ; elle s'exprime en mL.min
-1.kg
-1.
La puissance
maximale aérobie P
MA peut être déterminée à partir de la
valeur de V
O2max = 51,4
mL.min-1.kg-1
grâce à la formule
empirique de Hawley .
VO2max
=(0,01141 PMA +0,435) x1000 / M avec M masse du cycliste.
.
Lors d'un entraînement très intense, et après échauffement, le sportif
choisit de développer
une puissance P
MS à la limite d'un seuil qui équivaut
environ à 85 % de la P
MA. Au-delà de
cette valeur, le cycliste travaille en zone dite "anaérobie" ; il
s'épuise très rapidement et
récupère plus lentement.
Cette partie consiste à déterminer les vitesses d'un cycliste au seuil
anaérobie dans deux
situations : sur un sol plat, puis lors de l'ascension d'un col de
pente moyenne 10%.
Pour modéliser ces deux situations, on assimilera le système « vélo +
cycliste » à un point
matériel (son centre de gravité G). On admettra que le couple moteur
exercé par le cycliste au
niveau des pédales se traduit par une force motrice parallèle au
déplacement, notée F
m appliquée à ce système.
Deux types de frottements sont considérés :
- les forces de résistance dues à l'air,
notées F
air = 0,20 v
2 ( v : vitesse du vélo)
- les forces de résistance au roulement, notées F
r= 0,004 P
( P poids du vélo m=10 kg+ cycliste M = 75 kg).
Les roues ne glissent pas et la vitesse du vent est négligeable.
1. Définir la puissance
d'une force et exprimer la relation entre la puissance motrice P
m,
la
force motrice F
m et la vitesse v du cycliste. lndiquer les
unités des grandeurs en jeu.
La puissance ( watt) ets égale au produit scalaire du vecteur force (N)
par le vecteur vitesse ( m /s).
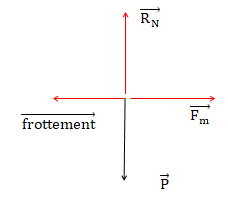
2. Le cycliste roule sur
un terrain horizontal. Représenter sur votre copie, au niveau du centre
de gravité G du système " vélo + cycliste ", les forces survantes : le
poids P
de l'ensemble, la réaction normale du sol R
N, les forces de
frottement, ainsi que la force
motrice F.
.
3. À partir de la
deuxième loi de Newton, exprimer littéralement F. en fonction notamment
de la vitesse v lorsque le cycliste roule à vitesse constante sur un
terrain horizontal.
Le mouvement étant rectiligne uniforme sur route horizontale : F
m
=
Fair + Fr =0,20 v2 +0,004 P.
4. En
déduire une expression littérale de la puissance P
m
développée par le cycliste en
fonction de la vitesse v et des constantes fournies.
La force motrice et le vecteur vitesse étant colinéaires et de même
sens : P
m = F
m v =(
0,20 v2 +0,004 P)v.
5. Montrer que la
puissance maximale
développée par le cycliste au seuil anaérobie, notée P
MS,
vaut 0,26 kW.
VO2max
= 51,4 mL.min-1.kg-1 = 51,4 10-6
/ 60 =8,57 10-7 m3 s-1 kg-1.
51,4=(0,01141 PMA +0,435) x1000 / 75.
PMA =0,304 kW.
PMS = 0,85 PMA = 0,304 x0,85 =0,26 kW.
6.
On donne la courbe
correspondant à la puissance motrice développée en fonction de la
vitesse v
1, sur route
horizontale. Déterminer graphiquement la valeur v de la vitesse, pour
la puissance de
seuil anaérobie P
MS de ce cycliste. .Justifier que les
frottements de I'air ne peuvent être négligés dans ce modèle.
7. Le cycliste
aborde désormais l'ascension sur une route inclinée d'un angle
a, avec
l'horizontale. Donner la nouvelle expression de F
m dans
cette situation et montrer que la
puissance développée par le cycliste devient P
m= 0,20 v
3
+ (M +m)(0,004+ sin
a)gv.
Fm = Fair + Fr =0,20 v2 +0,004 (M+m)+
(M+m) g sin a.
Pm=Fm v= 0,20 v3 + (M
+m)(0,004+ sin a)gv.
8. Déterminer la
valeur de la vitesse v
2 pour la puissance au seuil anaérobie
P
MS pour une
montée avec une pente à 10 %, c'est-à-dire une élévation de 10 m pour
un déplacement
de 100 m à I'horizontale. On pourra s'appuyer sur Ie graphe précédent
en modifiant la
courbe en conséquence, ou bien utiliser une calculatrice.
tan
a ~ sin
a ~0,1.
260 =
0,20 v3 + 85(0,004+ 0,1)*9,8v.
260 =0,20 v3 +86,6 v.
v3 +433 v -1300 =0 ; v2 ~3 m /s.
9. Exprimer v
1
et v
2 en km.h
-1, arrondies au km.h
-1
près, et commenter les résultats.
v
2 =3 x3,6 ~11 km / h.
10. On admet que, sur
route horizontale, la vitesse du cycliste est voisine de v= 10 m.s
-1.
Déterminer le nombre de tours de pédales par minute (appelée cadence)
que doit
respecter le cycliste pour obtenir cette vitesse avec le développement
choisi1 (taille du plateau et taille du pignon). On pourra s'appuyer
sur la relation
suivante :
vitesse (m.min
-1) = cadence (tr.min
-1) x
développement (m).
Circonférence des roues : 2,115 m.
Sur route horizontale : N
1 = 54 dents du plateau ; N
2
= 16 dents du pignon. Développement 7,27 m.
En montée : N
1 = 34 ; N
2 = 28.
Développement 2,62 m.
Le développement est la distance parcourue par le cycliste à chaque
tour de pédale : N
1 / N
2 x circonférence de la
roue.
Cadence = 10 x 60 / 7,27 ~83 tr / min.
11. À puissance
constante, justifier l'intérêt de faire varier le rapport N
1
/ N
2 lors de la montée.
Cadence = 3 x
60 / 2,62 ~69 tr / min.
On fournit moins deffort pour faire tourner la roue.
B : Le
glucose. une source essentielle d'énerqie.
Lors de la pratique d'un sport, l'énergie nécessaire à
l'organisme est introduite au niveau
cellulaire par des transformations chimiques mettant en jeu le glucose.
Le glucose existe sous
différentes formes, la forme cyclique étant la plus courante.
Les molécules de glucose.
12. Donner la définition
d'un isomère.
Deux isomères possèdent la même formule brute mais des formules
développées différentes.
13. Déterminer le
nombre de carbones asymétriques dans la molécule de glucose de forme
cyclique (D-g lucopyranose).
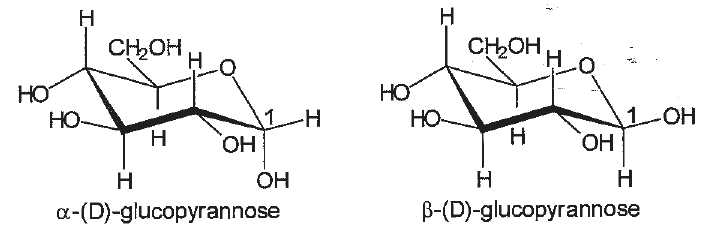
5 atomes de carbone asymétriques.
14. Préciser ce qui différencie les
deux isomères
a
et ß du D-glucopyranose. Préciser à quel
type d'isomérie correspondent ces deux formes.
Seul la configuration du carbone n°1 diffère : ce sont deux
diastéréoisomères.
15. Préciser comment sont
polarisées les liaisons O-H dans cette molécule. Proposer une
structure de Lewis pour cette dernière.
L'atome d'oxygène est plus électronégatif que l'atome d'hydrogène.
l'atome d'oxygène porte une charge négative partielle.
16. Le glucose est très
soluble dans l'eau (900 g.
L-1), ce qui permet le transport
par le sang ;
en effet, celui-ci est constitué à 90 % d'eau. En analysant la
structure de la molécule,
donner une explication de cette solubilité élevée du glucose dans l'eau.
La molécule de glucose est polaire ; la molécule d'eau est polaire : le
glucose est donc très soluble dans l'eau.
Le dosage d'une solution de
glucose par la liqueur de Fehling.
17. Expliquer le principe
général d'un dosage par comparaison.
Phase 1 : dosage du glucose de concentration connue d'une
solution dite de référence par la liqueur de Fehling.
Phase 2 :
dosage du
glucose de concentration inconnue de la solution étudiée par la
liqueur de Fehling.
18. Compléter le schéma
du dosage (nommer le matériel et les réactifs utilisés).
 19.
19. Compte-tenu des
pictogrammes de sécurité de la liqueur de Fehling, préciser les mesures
de sécurité particulières à prendre.
Corrosif : port de blouse, gants et lunettes.
Dangereux pour l'environnement : ne pas jeter à l'évier.
20. Proposer
un intérêt possible du chauffage lors de ce dosage.
La température est un facteur cinétique ; en chauffant on accélère la
réaction.
21. A partir de
l'équation du dosage et des données, déterminer la
relation à l'équivalence entre la quantité de glucose versé et la
quantité d'ions cuivre (ll)
consommés, et en déduire la valeur de la quantité de glucose nécessaire
pour faire réagir
tous les ions cuivre (ll).
C
6H
12O
6 +5HO
- +2CuT
22---->
C
6H
11O
7-+Cu
2O(s)
+4T
2- +3 H
2O.
n(glucose ) =0,5 n(
CuT22-).
40 g CuSO
4,5H
2O dans 1,0 L d'eau soit 40 / M(
CuSO4,5H2O)=40
/ 249,7 =0,160 ~0,16 mol.
n(glucose )
=8,0 10-2 mol.
22. Déterminer les
valeurs attendues de V
éq1 et V
éq2 pour les deux
étapes de ce dosage.
Solution de glucose de référence C
m = 4,0 / 180,1 ~0,0222
mol / L.
V = 10mL de liqueur de Fehling. [
CuT22-] = 0,16 mol / L
V [CuT22-]
=2 Véq1 Cm ; Véq1 = 10 x0,16 /
(2x0,0222) ~36 mL.
Solution S0 diluée 10 fois : V [CuT22-]
=2 Véq2 0,1C ;
Véq2 = 10 x0,16 / (0,2 C).
Solution S0
: 3,9 g de glucose dans 100 mL: C =3,9 / (180,1 x0,100)=0,216 mol / L
Véq2 = 10 x0,16 / (0,2 x0,216) =37 mL.
L'assimilation du
glucose dans le corps.
On cherche à déterminer l'énergie « récupérable » par la
dégradation du glucose de la boisson, On modélise cette dégradation par
une équation de réaction (E) où du
dioxygène gazeux, avec le coefficient stæchiométrique unité, réagit
avec le glucose solide
pour former du dioxyde de carbone gazeux et de l'eau liquide.
23. Écrire cette
équation de réaction (E). Préciser à quel
processus biologique elle correspond.
1 / 6 C6H12O6
(s)+O2(g) --->CO2(g)+H2O(l).
Processus aérobie.
24. Déterminer
l'enthalpie standard de réaction
DrH° à 298 K associée à (E),
à partir des
enthalpies standard de formation et des coefficients stæchiométriques
algébrisés.
DrH° =DrH° (CO2 g) +DrH° (H2O
l)-DrH°
(O2 g)-1 / 6 DrH° (glucose s).
DrH° = -393,5-285,1 -0+1274
/ 6 = -466,3 kJ / mol.
25.
Déterminer l'enthalpie libre standard de réaction
DrG° à
298 K associée à (E) sachant que
DS° =
+259 J.mol
-1.K
-1.
DrG°=DrH°-TDS° = -466,3 103 -298 x 259 = -5,43 105
J.mol-1.
26. On suppose que
l'énergie « récupérable » par unité de quantité de matière en glucose
dégradé est l'enthalpie libre standard de la réaction précédente. En
déduire
l'énergie « récupérable>> correspondant aux 100 mL de la boisson.
Comparer la valeur obtenue avec celle de 71 kJ indiquée sur l'étiquette
pour 100 mL
Dans 100 mL de la boisson, il y a 3,9 / 180,1 =.0,0216 mol de glucose.
Energie correspondante : 0,0216 x 5,45 10
5 =1,2 10
4
J = 12 kJ.
Valeur très inférieure à celle affichée.