Mathématiques,
Caplp maths sciences 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Exercice 1.
Dans cet exercice f désigne la fonction définie, pour.x réel, par f(x) = 1 /[x(x+1)].
On note C, la courbe représentative de f dans un repère orthonormé.
Partie A : Étude de la fonction f.
1. Déterminer l'ensemble de définition D de la fonction f.
Le dénominateur ne doit pas être nul : x diffère de zéro et de -1.
D = ensemble des réels moins 0 et -1.
a. Montrer que f est dérivable sur D et que f '(x) = (-2x-1) / [x(x+1)]2.
f est le quotient de fonctions dérivables non nulles : f est dérivable sur D.
On pose u = 1 et v = x(x+1) ; u' = 0 ; v' = x+1 +x = 2x+1
f '(x) = -(2x+1) / [x(x+1)]2.
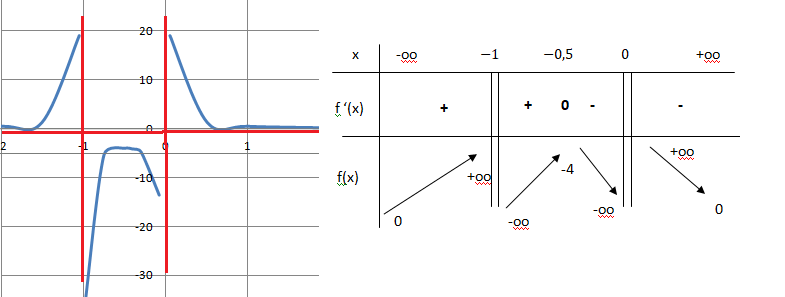
b. Donner le tableau de variations de f.
c. Déterminer les droites asymntotes.
d. Donner I'allure de C.
Quand x tend vers ± oo ; f(x) tend vers zéro. L'axe des abscisses est asymptote.
Quand x tend vers 0 +, f(x) tend vers +oo.
Quand x tend vers 0-, f(x) tend vers -oo. L'axe des ordonnées est asymptote.
Quand x tend vers -1+, f(x) tend vers -oo.
Quand x tend vers -1-, f(x) tend vers +oo.
La droite d'équation x= -1 est asymptote.
 3.
3. Montrer que C admet un axe de symétrie qui admet une équation de la forme x = k.
f(-0,5+x) = 1 / |(-0,5+x)(x+0,5)]
f(-0,5-x) = 1 / |(-x-0,5)(-x+0,5)] = 1 / |(-0,5+x)(x+0,5)]
f(-0,5+x) = f(-0,5-x).
C est symétrique par rapport à la droite verticale d'équation x = -0,5.
4. Déterminer une équation de la droite T tangente à la courbe C au point d'abscisse 1.
Coefficient directeur f '(1) = -0,75.Le point de coordonnées (1 ; f(1) =0,5) appartient à T.
y = -0,75 x +b
0,5 = -0,75 +b ; b = 1,25.
y = -0,75 x+1,25.
5. Déterminer les coordonnées du point d'intersection, noté A, de la droite T avec l'axe des
abscisses.
y = 0 =-0,75 x A+1,25 ; x A = 5 / 3.
6. Déterminer une équation de la droite passant par les points A et B, où B est le point de
coordonnées (1, -2).
y = ax +b ; 0 = 5a / 3 +b ; b = -5a /3.
-2 =a+b = a -5a/3 =-2a / 3 ; a = 3. ; par suite b = -5.
y = 3x-5.
7. Donner une équation de la droite d orthogonale à la droite (AB) et passant par B.
y = -x / 3 +b.
-2 = -1 /3 +b ; b = -5 /3.
y = -x/3 -5/3.
8. On note C le point d'intersection de la droite d avec l'axe des ordonnées. Déterminer l'aire
du triangle (ABC) en unité d'aire.
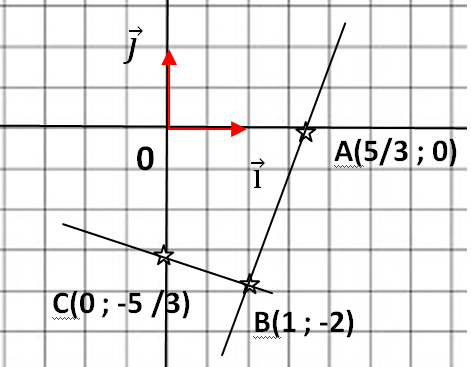
AB = [4 / 9 +4] ½ =(40 / 9) ½ =2 10 ½ / 3.
BC = [1 / 9 +1]½ =(10 / 9)½ = 10½ / 3.
AB x BC / 2 = 10 / 9 unités d'aire.
Partie B : Calcul intégral.
9. a. Déterminer les réels a et ß tels que, pour tout x €]0, +oo[, 1 / (x 2+x) = a /x +ß /(1+x).
En déduire une primitive de la fonction f sur ]0, +oo [.
Réduire au même dénominateur :
[(1+x) a +ßx ] / (x+x 2) = [ a +(a+ß)x ] / (x+x2)
Identifier : a +1 ; ß = -1.
f(x) = 1 /x -1 /(1+x).
F(x) = ln(x) -ln(1+x) + Cste.
10. Vérifier que la fonction F définie, pour x appartenant à ]0, +oo[, par
F(x)= -ln(1+1/x)
est une primitive de f sur ]0, +oo[ .
F(x) = -[ln(x+1) -ln(x)] = - ln[(1+x) / x] = -ln(1 +1/x).
11. Déterminer le réel m > 0 tel que l'intégrale suivante soit égale à 1.
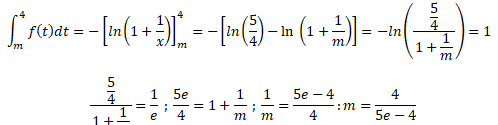 Partie C : Équations différentielles
Partie C : Équations différentielles.
Soit h la fonction définie sur ]0, +oo [ par
h(x) = x sin(x).
12. Déterminer les primitives de h sur ]0, +oo[.
Intégration par parties en posant u =x et v' = sin x ; u' = 1 ; v = -cos x. 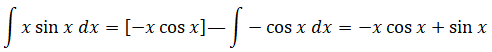
Primitives de h(x) : H(x) = sin x -x cos x + Cste.
13. a. Résoudre sur ]0, +oo[ l'équation différentielle y ' +y/ (x 2+x) = 0.
dy /dx = - y/ (x2+x) ; dy / y = - dx/(x2+x).
ln y = ln(1+1 /x).
y =1 +1 /x + C . ( C est une constante).
. b. Résoudre sur ]0,+oo[ l'équation différentielle y ' +y/ (x2+x) =(x+1) sin x. (E)
On cherche une solution de la forme C(x) (x+1) / x.
On dérive : C'(x) (x+1) / x - C(x) / x2.
Repport dans (E) : C'(x) (x+1) / x - C(x) / x2 +C(x) / x2 =(x+1) sin x.
C'(x) = x sin (x) ; soit C(x) = H(x) = sin x -x cos x.
Solution générale de (E) : ( sin x -x cos x) (x+1) / x + Cste.
c. Déterminer la solution u de l'équation différentielle (E) telle que u( p/2) = 0.
( sin p/2 -p/2 cos p/2) (p/2+1) / (p/2) + Cste = 0.
1+2 / p + Cste = 0 ; Cste = -1-2/ p.
u(x) =( sin x -x cos x) (x+1) / x -1-2/ p.
|
...
|
....
|
Partie D : Étude d'une suite définie par récurrence
14. Montrer qu'il existe un unique réel l tel que f (l)
= l.
x = 1 /[x(x+1)] ; x2(x+1) = 1 ; x3+x2-1=0.
Etude de g(x) = x3+x2-1.
g '(x) = 3x2+2x =x(3x+1).
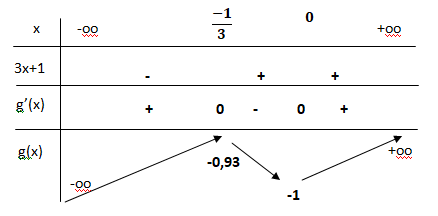
D'après le tableau ci-dessus, g(x) = 0 admet une unique solution.
15. Montrer que l appartient à [0,5 ; 1].
Sur cet intervalle, g(x) est continue, strictement croissante de g(0,5) = -0,625 à g(1) = 1.
zéro est compris entre -0,625 et 1 : donc l appartient à [0,5 ; 1].
16. a. On considère le code Python suivant :

Exécuter « à la main >> la commande suivante en détaillant itération par itération les
valeurs prises par les variables x, y et c ainsi que le résultat final obtenu :
>>> dichotomie(0,05).
x
|
0,5
|
0,375
|
0,6875
|
0,6875
|
0,6875
|
y
|
1
|
1
|
1
|
0,844
|
0,766
|
y-x > 2*0,05 =0,1
|
Vrai
|
Vrai
|
Vrai
|
Vrai
|
Faux
|
c
|
0,375
|
0,6875
|
~0,844
|
~ 0,766
|
0,727
|
g(c)=1 /(c2+c) -c
|
~ 1,56 > 0
|
~ 0,174 >0
|
~ -0,20 < 0
|
-0,027 < 0
|
|
b. Exptiquer ce que représente le résultat obtenu à la question précédente dans le
contexte de l'exercice.
Le résultat donne le réel l tel que f (l)
= l.
c. Justifier que, pour toute valeur strictement positive de eps, la boucle while du
programme s'arrête au bout d'un nombre fini d'itérations.
La fonction h(x) = x3+x2-1 est strictement croissante sur |0,5 ; 1] de h(0,5) = -0,625 à h(1) = 1.
y-x < 1 ; si eps < 0,5, on parcourt la boucle, y décroît et x croît. y-x tend vers zéro et on sort de la boucle.
Si eps > 0,5, on sort de la boucle.
17. Soit f :]0 ; +oo[ --> R la fonction définie par : f(x) = f o f (x) - x.
a. Calculer f(l).
f (f (l))-l ; f (l) = l ;
f (f (l))= f (l) = l ; f(l) =0.
b. Établir le tableau de signe de f sur ]0, +oo[.
( f o f (x) - x.) ' =f '(f(x) * f '(x) -1.
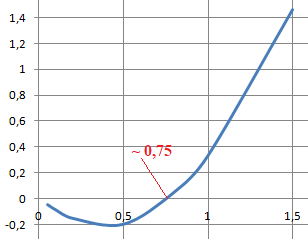
On considère la suite (un) définie par la donnée de son premier terme u0 et par la relation de
récurrence, un+1 = f (un).
18. Montrer par récurrence que la suite (un) est bien définie si et seulement si u0 appartient au domaine D de définition de f.
D = R -{0 } et - {-1}.
f(x) appartient à ]-oo ; -4] union ]0 ; +oo[.
f(x) appartient donc à D. L'intervalle J = ]-oo ; -4] union ]0 ; +oo[ est stable par f.
Initialisation : si u0 appartient à D, alors f(u0)= u1 appartient à D. La propriété est vraie au rang 1.
Hérédité : la propriété est supposée vraie au rang n.
un appartient à D. f(un)=un+1 existe.
Or J est stable par f, donc f(un+1)=un+2 existe.
Conclusion : la propriété est vraie au rang n et héréditaire, elle est vraie pour toutes valeurs de D.
19. On suppose dans cette question que u0 appartient à ]0, +oo[.
a. Montrer que la suite (un) est bien définie.
f(x) appartient donc à ]0, +oo[. L'intervalle ]0, +oo[ est stable par f.
Donc la suite (un) est bien définie.
b. Montrer que les sous-suites (u2k ) et (u2k+1) sont monotones.
Sur cet intervalle ]0, +oo[, la fonction f est strictement décroissante.
Donc les sous suites paire et impaire sont monotones.
c. Étudier la convergence de la suite (un) en fonction de u0.
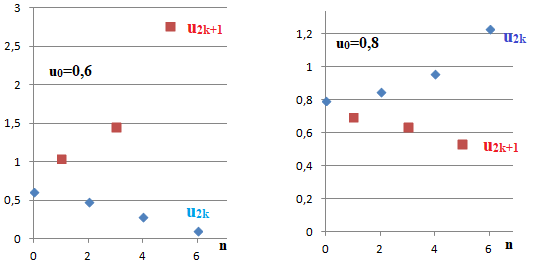
Si u0 ~0,754, la suite est constante.
20. On suppose dans cette question que u0 appartient à l'intersection de D avec ]-oo ; 0]. Étudier la convergence de la
suite (un) en fonction de uo.
Exercice 2.
Préciser si chacune des propositions suivanfes esf vraie ou fausse, puis justifier la réponse.
Une réponse non justifiée ne rapporte aucun point.
1. La population d'une ville a augmenté de 10 % en quatre ans.
Proposition. On peut dire que la population de cette ville a augmenté de 2,5 % par an en
moyenne. Faux.
Initial : la population vaut 1. Elle croît de x % par an.
Au bout d'un an, la population vaut 1+0,01 x.
Au bout de 2 ans, elle vaut : (1+0,01x)2.
Au bout de 4 ans, elle vaut : (1+0,01x)4 = 1,10.
1+0,01 x = 1,024 ; x = 2,41 %.
2, Soit f la fonction définie, pour tout réel x non nul, par f(x)=(1- cos(x)) / x2.
Proposition. La fonction f tend vers 1 quand x tend vers 0. Faux.
Développement limité de cos (x) en zéro : cos (x) = 1-x2/2 +x4/24 +...
1- cos(x) = x2/2 -x4/24 +...
(1- cos(x)) / x2 = 0,5 -x2/24 +...
f(x) tend vers 0,5.
3. Soit n un entier naturel non nul.
Proposition.
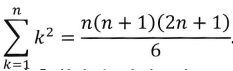 Vrai. Vrai.
Démonstration par récurrence :
Initialisation : c'est vrai pour n = 1.
Hérédité : c'est supposé vrai pour n.
12 +22 +...+n2 + (n+1)2 =n(n+1)(2n+1) / 6 + (n+1)2 =(n+1) [n(2n+1) / 6 +n+1].
(n+1) [2 n2+ 7n +6 ] / 6.
Or 2 n2+ 7n +6=(n+2)(2n+3).
Par suite : 12 +22 +...+n2 + (n+1)2 =(n+1)(n+2)[2(n+1)+1] / 6. La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est vraie pour tout entier n.
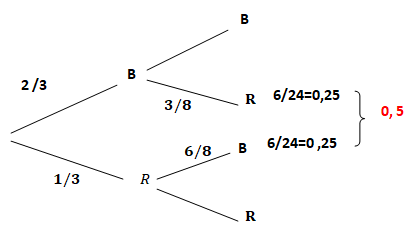
4. Une urne contient six boules bleues et trois boules rouges. On prélève simultanément
deux boules dans l'urne. Tous les prélèvements sont supposés équiprobables.
Proposition. La probabilité que les deux boules soient de couleurs différentes est égale à 0,5. Vrai.
Nombre de tirages possibles : 9 x 8 / 2 =36.
Nombre de tirages bicolores : 18.
18 / 36 = 0,5.
Autre approche :
On numérote les boules bleues; B1, B2 ... B6. et les rouges R1, R2 et R3.
Tirer 2 boules simultanément équivaut à les tirer individuellement et successivement sans tenir compte de l'ordre.
5. Deux variables aléatoires X et Y sont indépendantes et suivent respectivement les lois
normales N (24 ; 4 ) et N(20; 2). On admet que la variable aléatoire Z = X +Y suit une loi normale.
Proposition. L'espérance mathématique et l'écart type de Z sont respectivement 44 et 6. Vrai.
µ = 24 +20 = 44 ; s = 4+2 = 6.
6. Pour tout réel q, on considère ta matrice 
Proposition. ll existe q réel. tel que 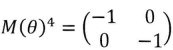 Vrai (q = p /4). Vrai (q = p /4).
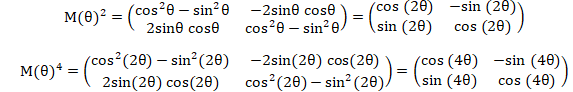
q = p /4.
7. Dans le plan muni d'un repère orthonormé, on considère les points A(0;1) , B(0;2) et
C(1; -1). On note G le barycentre du système (A, 1) ; (B , -1) ; (C ,2).
Proposition. Les coordonnées du point G sont (2; -3).
Faux.
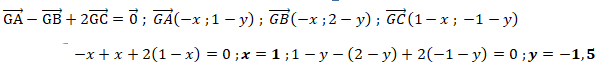
8. Dans l'espace rapporté à un repère orthonormé, on considère :
- la sphère S d'équation x2 + y2 + z2 =3 ;
- la droite D passant par le point A de coordonnées (-1; 1 ;0) et dirigée par le
vecteur directeur de coordonnées (1; 0; 1).
Proposition. La droite D est tangente à la sphère S. Faux.
Equation paramétrique de la droite :
x = t-1 ; y = 1 ; z = t avec t réel.
Repport dans l'équation de la sphère :
(t-1)2 +1+t2 =3.
t2+1-2t+1+t2 =3.
2t2+2-2t = 3 ; 2t2-2t -1=0.
Discriminant : 4+8=12 ; solutions ; t = (2 ± 2*3½) / 4.
Il y a deux points d'intersection.
|
|