Pasteurisation
du lait, étamage d'une cuve en cuivre,
concours CAPLP maths sciences 2022
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
Partie B :
Pasteurisation.
La pasteurisation du lait avant la mise en bouteille se fait dans une
cuve en cuivre. Le contrôle de la température se fait à l’aide d’un
dispositif électronique basé sur une thermistance .
Partie B-1 : La
thermistance.
22. Donner une
brève définition d’une thermistance.
Une thermistance est un composant électronique dant la résistance varie
en fonction de la température.
On donne l’équation générale de la résistance d’une thermistance CTN :
R = R0 exp(B(1 / T-1/T0)).
T : température ambiante en K
T0 : température de référence à 25 °C (soit 298 K)
R0 : résistance à 25 °C
B : indice de sensibilité thermique
23. Donner la
dimension de B. Une justification est attendue.
Le terme en exponentielle est sans dimension, donc B / T est sans
dimension ; B est en kelvin.
24. Que signifie
CTN ? Donner l'allure de l'évolution de la valeur de la résistance en
fonction de la température pour une thermistance CTN.
CTN : coefficient de température négatif.
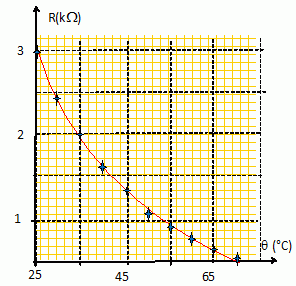 25. Proposer un protocole
expérimental qui permet de représenter graphiquement cette évolution.
25. Proposer un protocole
expérimental qui permet de représenter graphiquement cette évolution.
On utilise le montage en pont de Wheststone
suivant :
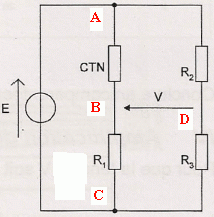
On veut choisir judicieusement les résistanes R 1, R 2
et R 3 de manière à linéariser l'évolution de V en
fonction de la température.
Pour linéariser la mesure, on impose V=0 pour q = 25°C, V = 1 V pour q = 50°C et V= 2 V pour q = 75°C.
Partie B 2 : La cuve en
cuivre
B 2.1 Étude structurale.
Le cuivre pur cristallise dans le système cubique à faces centrées.
Le rayon d’un atome de cuivre est d’environ 130 pm.
26. Représenter la
maille élémentaire du cuivre pur (vue en perspective cavalière ou en
projection). Déterminer le nombre d’atomes par maille.
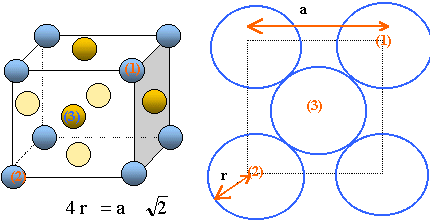
- Chaque atome situé au centre d'une face, donc
commun à deux mailles compte pour ½ : il y a 6 faces soit 6*0,5 = 3
atomes.
- Chaque atome situé à un sommet, donc commun à huit
mailles compte pour 1/8 : il y a huit sommets donc 8 /8= 1 atome.
27. En adoptant le
modèle de sphères dures indéformables, déterminer la valeur de la masse
volumique du cuivre. Comparer avec la valeur donnée 8960 kg m-3
et critiquer.
Masse des 4 atomes de cuivre : m= 4 x M(Cu) / NA =4 x0,0635
/ (6,02 1023) =4,2 10-25 kg.
a = 4 x130 10-12 /1,414 ~3,68 10-10 m ; volume de
la maille : V =(3,68 10-10)3 ~4,97 10-29
m3.
m / V =4,2 10-25
/ (4,97 10-29)=8,4 103 kg m-3.
Ecart relatif avec la valeur donnée :(8,96 -8,4) / 8,96~0,06 ( 6 %).
Les
entités de cuivre ne sont pas des sphères parfaites.
Par
ailleurs, le cuivre peut former de nombreux alliages, par insertion ou
substitution.
B 2.2 : Capacité thermique du cuivre.
28. Donner, en le justifiant, la fonction
d’état adaptée à la transformation s’effectuant à la pression
atmosphérique lors de l’étalonnage du calorimètre.
A pression constante, la fonction adaptée est l'enthalpie.
29. À l’aide des données numériques fournies, déterminer puis calculer
la capacité thermique Cc du calorimètre (incluant agitateur,
thermistance et résistance chauffante).
Une masse me d’eau me=0,600 kg, de capacité thermique massique ce=4 185 J kg-1 K-1
est introduite dans le calorimètre et une résistance chauffante (de
résistance électrique r=230 ohms) y est immergée, sans être alimentée
dans un premier temps. Après équilibre, la température de l’ensemble
eau calorimètre est θi=23,2°C. La résistance chauffante est
ensuite alimentée sous une différence de potentiel U=120 V et, au bout
d’un temps Δt=9 min, la température de l’ensemble atteint la valeur
d’équilibre θf=36,1°C. Les fuites thermiques sont négligées.
Energie électrique fournie : U I Dt =U2 / r Dt = 1202 /230 x9 x60=3,38 104 J.
Energie reçue par l'eau et le calorimètre : (me ce +Cc)(θf -θi)=(0,600 x4185+Cc) x12,9=3,24 104 +12,9 Cc.
3,38 104 =3,24 104 +12,9 Cc ; Cc ~109 J K-1.
30. Déterminer puis calculer la capacité thermique massique du cuivre
cCu.
Un échantillon parallélépipédique de cuivre de masse mcu (aire de la section S=25 cm2, épaisseur L=3 cm, masse volumique ρ Cu=8960 kg m-3) et de capacité thermique massique ccu est introduit dans un four régulé en température où il atteint, après équilibre, la température θ1=250°C.
Cet échantillon est ensuite plongé le plus rapidement possible dans le
calorimètre qui renferme toujours la même masse d’eau me à la température initiale θi
(la résistance chauffante n’est plus alimentée) ; après fermeture,
l’ensemble {calorimètre + eau + échantillon} atteint la température
d’équilibre θ2=43,8°C.
Masse de cuivre m = S L ρ Cu=25 10-4 x0,03 x8960 =0,672 kg.
Energie cédée par le cuivre : m ccu (θ2 -θ1)=0,672 x(-206,2) ccu = -138,56 ccu J.
Energie gagnée par l'eau et le calorimètre : (me ce +Cc)(θ2 -θi)=(0,600 x4185+109) x20,6=5,4 104 J.
Système adiabatique : 5,4 104 -138,56 ccu = 0 ; ccu =3,9 102 J kg-1 K-1 .
B 2.3 : Corrosion du cuivre.
On étudie la corrosion de la cuve en cuivre à pH = 7 en milieu humide
aéré.
31. Écrire la réaction pouvant s'effectuer entre le cuivre et le
dioxygène dissous dans la solution aérée et calculer sa constante
d'équilibre à 298 K. On choisira une écriture de la réaction telle que
le coefficient stoechiométrique du dioxygène soit 1.
2Cu(s) = 2Cu2+aq + 4e-. E°1 = 0,34 V.
O2(g) + 4H+ + 4e- = 2H2O(l). E°2 = 1,23 V.
2Cu(s) +O2(g) + 4H+ = 2Cu2+aq +2H2O(l).
K = [Cu2+]2 / (PO2[H+]4).
E1 =E°1 +0,06 / 4 log [Cu2+]2.
E2 = E°2 +0,06 / 4 log (PO2[H+]4).
A l'équilibre E1 = E2 : E°1 +0,06 / 4 log [Cu2+]2 = E°2 +0,06 / 4 log (PO2[H+]4).
E°2 -E°1 =0,06 / 4 log K.
log K =4(1,23-0,34) / 0,06 =59,3 ; K =2,15 1059.
32. Déterminer la valeur du potentiel du couple O2(g)/H2O à pH = 7.
Pourquoi parle t on de surtension cathodique ?
E2 = E°2 +0,06 / 4 log (PO2[H+]4)= 1,23 -0,06 pH si PO2= 1 bar.
E2 =1,23 -0,06 x7 =0,81 V.
Pendant
l'électrolyse, au voisinage de la cathode les cations disparaîssent (
réduction de ces derniers ) : leur concentration diminue fortement au
contact de l'électrode. La loi de Nernst s'appliquant, le potentiel de
l'électrode diminue. L'électrolyse ne peut se poursuivre avec une
vitesse acceptable, qu'en augmentant la tension appliquée entre les
électrodes : c'est ce que signifie surtension.
33. Définir et estimer le potentiel mixte de la solution aérée.
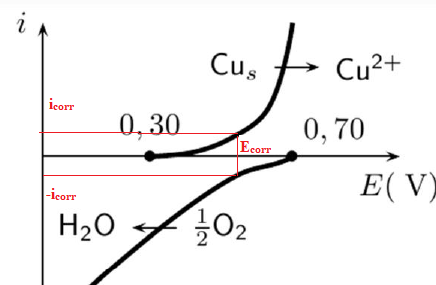
34. En fait, cette corrosion du cuivre est très lente. Que peut on en
déduire sur les valeurs des courants cathodiques et anodiques ?
Les valeurs des courants cathodiques et anodiques sont très faibles.
|
Partie B 3 : Étamage de la cuve.
L’électrolyse du cuivre consiste ici à déposer une fine couche d’étain
sur toute la surface du récipient. Ce procédé est appelé étamage.
Le récipient à étamer constitue une électrode, l’autre étant de l’étain Sn(s) pur.
L’électrolyte est constitué de sulfate d’étain, Sn2+(aq) + SO42- (aq) et de différents additifs que l’on négligera.
On étudie les réactions aux électrodes en considérant que le solvant n’intervient pas.
On considère le schéma du montage représenté ci-dessous.
35. Indiquer sur ce schéma le sens du courant électrique dans le
circuit ainsi que le sens de circulation des porteurs de charge dans
les conducteurs métalliques et dans la solution. On ajoutera les mots «
anode » ou « cathode » aux emplacements en pointillés.
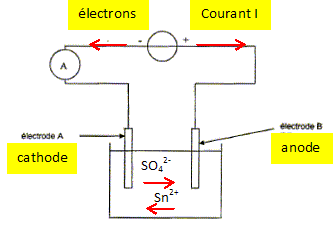
Les cations se déplacent dans le sens des
ions Sn2+aq et les anions
dans le sens des ions sulfate.
36. Écrire les demi-équations chimiques des transformations qui ont
lieu sur chaque électrode A et B et en déduire l’équation de la
réaction globale de cette électrolyse.
Réduction des ion étain(II) suivant :
Sn2+aq + 2e- =
Sn(s)cathode.
On observe un dépôt d'étain sur
l'électrode A : c'est le but recherché ; la
casserole à recouvrir constitue donc la cathode
A.
Le métal étain de
l'anode s'oxyde : Sn(s)anode =
Sn2+aq + 2e-.
Sn(s)anode =
Sn(s)cathode.
L’intensité du courant électrique est maintenue constante pendant toute la durée Δt de l’électrolyse et vaut I = 25 A.
37. Montrer alors que la durée de l’électrolyse peut être exprimée, en
fonction de la masse d'étain mSn déposée, par la relation
Δt=2.mSn.F / (I MSn).
Quantité de matière d'étain nSn = mSn / MSn.
Quantité de matière d'électrons : ne = 2 nSn = 2mSn / MSn= I Dt / F.
Δt=2.mSn.F / (I MSn).
On veut étamer la cuve cylindrique précédente en cuivre, de diamètre
intérieur D = 90 cm et de hauteur H = 70 cm. Le dépôt d’étain doit être
réalisé sur les seules faces internes et sur une épaisseur e = 20 μm.
38. Montrer que le volume à étamer de la cuve Vcuve=p.D e.( D /4 +H) et le calculer.
Surface du fond : pD2 / 4 ; surface latérale :pDH.
Surface totale d'étain : pD(D /4 +H).
Vcuve=p.D e.( D /4 +H) =3,14 x0,90 x20 10-6 (0,225+0,70)=5,23 10-5 m3.
39. Calculer la durée minimale de l’électrolyse pour réaliser ce dépôt.
Masse volumique de m'étain : 7300 kg m-3.
Masse d'étain mSn =5,23 10-5 x7300=0,382 kg.
Δt=2.mSn.F / (I MSn)= 2 x0,382 x96500 / (25 x0,119)=2,48 104 s ~6 h53 min.
|
|




