Mathématiques,
concours audioprotésiste 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Partie A. Exercice 1.
Définir et donner un exemple :
- d'un nombre entier:
un nombre entier ne contient ni décimale, ni fraction.
- d'un domaine de définition d'une fonction :
c'est l'ensemble des valeurs de x pour lesquelles f(x) existe.
- d'une fonction impaire.
f(x) = -f-(x), graphe symétrique par rapport à l'origine. Exemple f(x) = 1 /x.
Donner le domaine de définition de la fonction f(x) = sin(x)-1 / [(x2-x)½ -(x2+x)½].
Le dénominateur ne doit pas être nul.
(x2-x)½ différe de (x2+x)½ soit x différe de zéro.
De plus x2-x > 0 soit x < 0 ou x > 1.
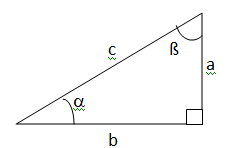
b : Compléter :
sin (½p-ß) = sin a.
cos (3p/2-a )= - cos ß
a +ß = ½p ; 3p /2 - a -ß =3p/2- ½p =p.
3p/2-a =p+ß.
cos ( p+ß) = - cos ß.
tan ( p/4 -p /2) = tan(-p/4) = -tan p /4 = -1.
sin (a +ß) = sin (p/2) = 1.
c. Encadré le nombre 1-2½ au dixième près.
racine carrée (2) = 1,414 ; 1-1,414 = -0,414.
-0,42 < 1-2½ < -0,41.
2.
a P(x) = -3x2 +5x -1.
Evaluer P(x) pour x = 3-3½.
-3(3-3½)2 +5(3-3½.)-1 = -3(9+3-6*3½+15-5*3½-1 = -36+18*3½+14-5*3½= -22+13*3½~0,517.
b Simplifier :
A = sin(-a) sin(90+a) / ( cos (180 +a) cos(270-a)).
sin(90+a) = sin a ; sin(-a)= - sin(a).
cos (180 +a)= - cos (a) ; cos(270-a) = - sin ( a).
A = - sin2(a) / (sin(a) cos(a)) = -tan (a).
B = sin(90-ß) tan(90 +ß) / (cos (180-ß) tan (270-ß)).
sin(90-ß) = cos(ß) ; tan(90 +ß) = sin(90+ß) / cos(90 +ß) =cos(ß) / (-sin(ß).
sin(90-ß) tan(90 +ß) =- cos2(ß) / sin (ß).
cos (180-ß) = - cos (ß) ; tan (270-ß) = sin( 270-ß) / cos(270-ß)= cos(ß) / sin (ß).
cos (180-ß) tan (270-ß))=- cos2(ß) / sin (ß).
B = 1.
3.1 Exprimer les angles suivants en radians.
270° = 3 p / 2radians ; .315° = 315 /180 x3,14 =1,75 p radians. 330° = 330 /180 x3,14 =11 p /6.
1 demi -tour = p radians ; un quart de tour = p / 2 radians. 5 demi-tours = 5 p radians.
3.2 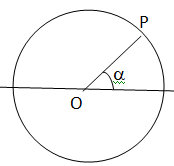 OP = 1 unité. OP = 1 unité.
Quelles sont les coordonnées du point P si :
a = 5 p /6 ; x = cos (5 p /6) = - cos (p /6)= -3½ /2 ; y = sin (5 p /6) = sin (p /6)=0,5.
a = -2 p / 3 ; x = cos (-2 p / 3) = -0,5 ; y = sin (-2 p / 3) = sin (-p / 3)= -3½ / 2.
3.3 Est-il possible de trouver un angle a justifiant les propriétés suivantes :
sin(a ) =0,75 et cos (a) = 0,25.
Non, car sin2a +cos2a = 1 ; cos2a = 1-0,752 =0,4375 différe de 0,252.
sin(a ) =0,25 et tan (a) = 0,2.
Non car : cos2a = 1-0,252 =1- 1 /16 = 15 /16 ; cos (a) = ±15½ / 4.
tan (a) =±1/ 15½ ~ ±0,258.
4. Résoudre les équations suivantes dans le troisième quadrant uniquement.
x appartient à [p ; 3 p /2].
sin(x-2) = 1 = sin (p/2)
x-2 =± p/2 +2kp ; x = ± p/2 +2kp +2.
k=0 ; x = p/2 +2.
2sin (ß) -1=0.
sin(ß) =0,5 = sin (p / 6 ) ou sin(5p/6)
ß = ± p /6 +2kp.
aucune solution entre [p ; 3 p /2].
sin (ß) = tan (ß) = sin(ß) / cos (ß) soit ß = 0 +2kp.
aucune solution entre [p ; 3 p /2].
Partie B.
1.a. Représenter graphiquement les fonctions suivantes : f(x) =| 3x-3| et g(x) =|x2-1|.
Si x < 1, f(x) = 3-3x ; si x > 1 , f(x) = 3x-3.
Si -1 < x < 1; g(x) = 1-x2 sinon g(x) = x2-1.
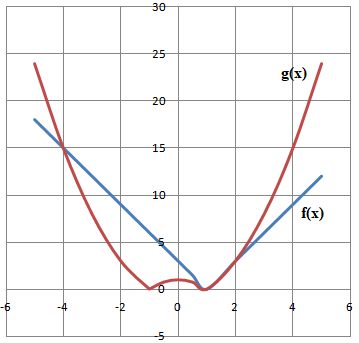
b. Déterminer l'antécédent de 5 par f.
3x-3=5 ; x = 8 /3.
c. Déterminer l'image de 3 par g.
g(3) = 32-1 = 8.
c. Etudier la croissance de f et de g sans calculer la dérivée.
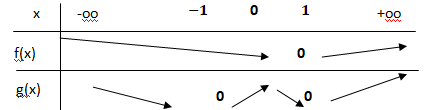
2.a Résoudre au moyen de 2 méthodes différentes.
20x / (x2+100) = -1.
20 x = -x2-100 ; x2+20+100 = 0.
(x+10)2 = 0 soit x = -10.
Discriminant D = 202 -4*100 = 0 solution unique x = -20 /2 = -10.
b Résoudre graphiquement le système d'inéquations suivantes :
-1 < x < 3.
-2 < y < 4.
x+y-5 < 0 soit x < 5-y.
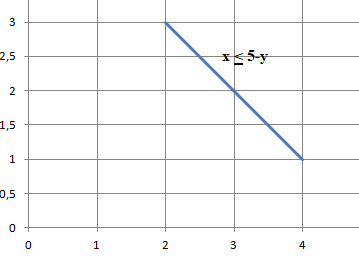
3. Simplifier.
A = ln[(5½+1) / 2] +ln[(5½-1) / 2]
A = ln[(5½+1)(5½-1) /4]ln[(5-1) /4] = ln(1) = 0
Quel est le domaine de la fonction suivante f(x) = [x-(x2+x-2)½] / [2x-(4x2-x]½].
(x2+x-2)½ doit être positif ou nul.
Solutions de x2+x-2 =0. Discriminant D =1+8=9 =32.
Solutions : x1 = (-1+3) / 2 =1 ; x2 = (-1-3) / 2 = -2
x2+x-2 >0 si x appartient à ] -oo ; -2 ] union [1 ; +oo[.
4x2-x > 0 ; racines de 4x2-x =0 ; x = 0 et x =0,25.
x appartient à ] -oo ; 0 ] union [0,25 ; +oo[.
2x-(4x2-x]½ ne doit pas être nul.
4x2=4x2-x ; x doit être différent de zéro.
x appartient à ] -oo ; -2 ] union [1 ; +oo[.
Préciser si les fonctions suivantes sont convexes ou non.
F(x) = - log(x+4) ; F '(x) = -1 /(x+4); F"(x) =1 /(x+4)2 >0, donc fonction convexe.
G(x) = 5-2x+3 = exp[(-2x+3) ln(5)].
G'(x) = -2 ln(5) exp[(-2x+3) ln(5)] .
G"(x) = (-2 ln(5))2 exp[(-2x+3) ln(5)] >0, donc fonction convexe.
|
...
|
....
|
4. Calculs de dérivées premières.
f(x) = -(2x)½ +(1-x) / x½.
Dérivée de -(2x)½ : -½ * 2 (2x)-½ = -(2x)-½.
Dérivée de (1-x) / x½.
On pose u = 1-x et v = x½ ; u' = -1 ; v' = ½x-½.
(u'v-v'u) / v2 =[-x½ -(1-x) / (2x½) ]/ x.
g(x) =sin4 (-3px+4).
On pose u =-3px+4 ; u' = -3p.
g'(x) = -12p cos (-3px+4) sin3 (-3px+4).
h(x) = 1 / sin( 4x-x2)1/3.
On pose u = ( 4x-x2)1/3 ; u'=1 /3 (4-2x) ( 4x-x2)-2/3 ;
w = sin( 4x-x2)1/3 ; w' =1 /3 (4-2x) ( 4x-x2)-2/3 cos( 4x-x2)1/3 ;
Dérivée de 1 / w = w-1 : -w' / w2 .
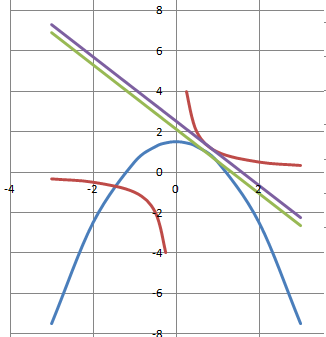
5. Tangente à une courbe donnée.
Représenter le graphe de chacune des fonctions. En quels points les
graphes de ces fonctions admettent-elles des tangentes parallèles.
f(x) = -x2+1,5 ; f ' (x) = -2x.
g(x) = 1 /x ; g '(x) = -1 /x2.
Les tangentes sont parallèles si elles ont le même coefficient directeur.
f '(x) = g'(x) ; -2x = -1 /x2 ; x3 = 1/2 ; x = 1 /21/3~0,793.
f '(0,793) =g'(0,793) ~ -1,59.
Equation de la tangente à la courbe représentant f(x) :
y = -1,59 x +b.
f(x) : le point de coordonnées 0,793 et f(0,793) ~0,87 appartient à la tangente.
0,87 = -1,59 *0,793 +b ; b =2,13.
y = -1,59 x +2,13.
g(x) : le point de coordonnées 0,793 et g(0,793) ~1,26 appartient à la tangente.
1,26 = -1,59 *0,793 +b' ; b' =2,52.
y = -1,59 x +2,52.
Recherche d'extrémum et de point d'inflexion.
Soit la fonction f polynomiale telle que f '(x) = (x+1)(x-2).
Esquiser le graphique sachant que f(2) = 3.
Justifier l'existence d'un point d'inflexion.
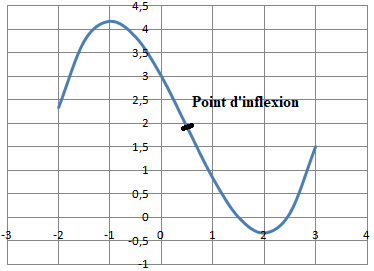
Dérivée seconde : on pose u =x+1 et v = x-2 ; u' = v' = 1.
u'v+v'u = x-2 +x+1 =2x-1.
f "(x) s'annule pour x = 0,5 et change de signe.
|
|