Autour de
l'astate, alpha-immunothérapie, concours agrégation
interne
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
L’isotope
211 de l’astate est un émetteur alpha. Dans le cadre de recherches
visant à l’utiliser en radiopharmacie, des études ont été menées pour
connaître ses propriétés chimiques et ainsi mieux comprendre le moyen
de le lier à des molécules vectrices.
Ce problème aborde l’établissement d’une partie du diagramme
potentiel-pH de l’astate ainsi que l’étude de certaines des espèces
chimiques qui y sont présentes.
L’astate : un élément
radioactif
L’astate, élément identifié en 1940, est l’un des plus rares éléments
naturels sur Terre. On estime à moins de 30 g la quantité totale
d'astate naturel dans la croûte terrestre. L’isotope le plus
intéressant pour son utilisation en radio-thérapie est l’isotope 211At.
Production d’astate 211.
L’astate 211 est fabriqué dans un cyclotron par irradiation d’une cible
en bismuth 209 à l’aide d’un faisceau de particules alpha d’énergie
égale à 28 MeV.
Q1. Après avoir
défini l’isotopie, donner la composition d’un atome de l’isotope 211 de
l’astate.
Deux isotopes ne diffèrent que par leur nombre de neutrons. Ils ont le
même numéro atomique Z.
21185At : 85 protons, 85 électrons et
211-85 =126 neutrons.
Q2. Donner la
composition d’une particule alpha. Proposer une équation traduisant la
formation de l’astate 211. Commenter.
42He particule alpha.
209 83Bi + 42He
--> 21185At
+2 10n.
La formation de l'astate 211 s'accompagene de la libération de 2
neutrons.
Désintégration d’astate 211.
La désintégration de l’astate 211 se fait selon deux voies différentes.
Chacune d’elles comporte une étape d’émission alpha et de capture
électronique. Cette dernière consiste en la transformation d’un proton
en un neutron par capture d’un électron du cortège électronique. Ce
type de réarrangement conduit à l’émission de rayons X.
Le schéma de la désintégration de l’astate 211 est donné.
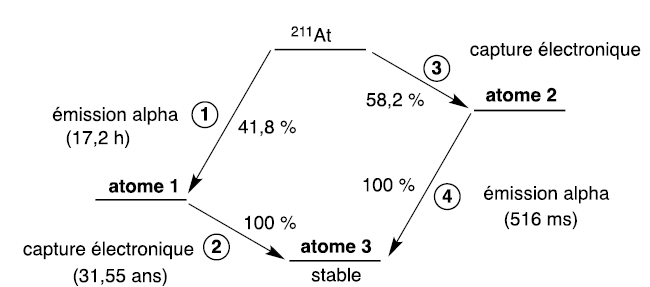
Q3. Déterminer les
atomes 1 à 3.
Atome 1 : 21185At-->
207 83Bi
+ 42He.
Suivie de : 207 83Bi
-->207 82Pb
( atome 3).
Atome 2 : 21185At-->21184Po
Suivie de : 21184Po--> 42He + 20782Pb.
Q4. Les désintégrations radioactives
suivent des cinétiques d’ordre 1 : établir la relation entre la
constante radioactive notée l et
le temps de demi-vie T. Le temps de demi-vie global de 211At
vaut 7,21 h. En déduire le temps de demi-vie manquant dans la figure.
L'activité s'écrit : A = -dN / dt = - l N.
N = N0 exp (-l
t).
N0 / 2 = N0
exp (-l T) ; ½ = exp (-l T) ; l T = ln 2.
Addition des activités : A(At) = 0,418 A(At) voie 1 +0,582 A(At) voie
3 .
lNAt=0,418
l1NAt
+ 0,582 l3NAt.
ln(2) / T=0,418 ln(2) / T1 +0,582 ln(2) / T3.
1 / 7,21 =0,418 / 17,2 +0,582 / T3 ; 0,582
/ T3 = 0,1387 -0,0243=0,1144.
T3 =0,582 / 0,1144 ~5,1 h.
L’astate : un élément chimique.
La configuration électronique de l’atome d’astate dans l’état
fondamental est :
1s22s22p63s23p64s23d104p65s24d105p66s24f145d106p5.
Q5. Donner le nom
des règles et principes qui ont permis d’établir la configuration
électronique fournie.
Préciser la colonne de la classification périodique dans laquelle se
situe l’astate et le nom de l’élément situé juste au-dessus.
Règle de Klechkowski et principe d'exclusion de Pauli.
La configurtion électronique se termine en 6p5 : l'astate
appartient à l'avant dernière colonne ( 17 eme), celle des
halgènes.
L'iode le précède dans cette colonne.
Q6. Un atome
d’astate est-il diamagnétique ou paramagnétique dans son état
fondamental ? Existe-t-il un état excité de l’astate dont la nature
magnétique est différente de celle de l’état fondamental ?
Répartition des électrons dans l'état fondamental :
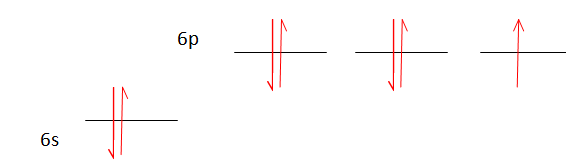
L'astate possédant un électron célibataire, son spin total n'est pas
nul : l'astate est paramagnétique.
L'astate possédant un nombre impair d'électrons, il n'existe pas d'état
excité de spin total nul : donc pas d'état excité diamagnétique.
Afin d’étudier les espèces de l’astate en solution aqueuse et de
simuler les effets dus à la solvatation, un calcul théorique du rayon
atomique de l’astate en solution est nécessaire. Le modèle théorique
utilisé est appelé UAHF (united atom Hartree-Fock). Pour les atomes
d’halogène, il existe une corrélation affine entre les rayons calculés
par le modèle UAHF et le rayon de Van der Waals. Ces valeurs sont
regroupées dans le tableau suivant, auxquelles ont été ajoutés les
rayons atomiques mesurés.
espèce
|
F
|
Cl
|
Br
|
I
|
At
|
rayon
UAHF ( pm)
|
150
|
198
|
208
|
235
|
|
rayon
de Van der Waals (pm)
|
146
|
182
|
185
|
204
|
209
|
rayon
atomique mesuré (pm)
|
50
|
100
|
115
|
140
|
|
Q7. Expliquer l’évolution du rayon
atomique mesuré du fluor à l'iode. Proposer une explication au fait que
pour chaque atome, le rayon de Van der Waals soit supérieur au rayon
atomique mesuré.
A chaque nouvelle période, les électrons occupant une couche
supplémentaire, ils prennent plus de place : le rayon atomique augmente.
Le rayon de Van der Waals ou rayon minimum d'approche de deux
atomes est très supérieur au rayon atomique du fait de la
répulsion des nuages électroniques des deux atomes.
Q8. En détaillant
votre démarche, proposer une valeur pour le rayon atomique de l’astate
qui s’accorderait avec le modèle UAHF.
Dans ce modèle UAHF, on cherche l'expression affine :
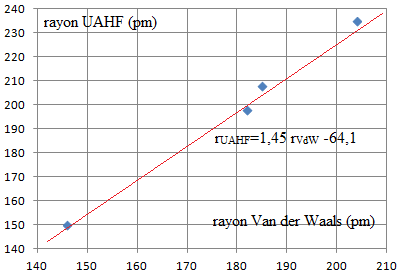
rUAHF=1,45 x209 -64,1 ~239
pm.
Établissement du diagramme
potentiel-pH de l’astate.
En milieu acide inorganique et dans la gamme de potentiels de stabilité
de l’eau, trois degrés d’oxydation de l’astate sont proposés selon le
potentiel de la solution. Nous les appelons par ordre croissant de
degré d’oxydation a,
ß et g. Pour
chacun de ces trois degrés d’oxydation, on recherche les différentes
espèces chimiques correspondantes. Dans ce but, des études précises ont
été réalisées.
Il n’existe qu’une seule espèce chimique de degré d’oxydation a correspondant à l'ion At-.
Détermination de la formule de l’espèce chimique de degré d’oxydation ß en milieu acide.
On note Ox la formule de l’espèce chimique de degré d’oxydation ß en milieu acide.
L’étude du couple oxydo-réducteur Ox / At– en milieu acide se fait à partir de l’étude des coefficients de partage entre l’eau et le toluène, définis par PA =[At- ]tol / [At- ]aq pour l’espèce At– et POx =[Ox ]tol / [Ox ]aq pour l’espèce Ox. On peut définir alors le coefficient de partage global de l’astate : P =([At- ]tol +[Ox ]tol) / ( [At- ]aq + [Ox ]aq ).
Cette grandeur est déterminée expérimentalement grâce à la radioactivité de l’astate. La figure 3 en
regroupe les valeurs trouvées.
Q13. À partir de la demi-équation électronique simplifiée At– = Ox + n e–, montrer que l’expression de P peut se mettre sous la forme : P =(PA + POxeu) / (1+eu) avec u = nF / (RT) (E-E°), où E° est le potentiel standard du couple rédox Ox/At– en solution aqueuse.
Relation de Nernst : E = E° + RT / (nF) ln ([Ox]aq / [At- ]aq) soit [Ox]aq = [At- ]aq eu.
P =( PA [At- ]aq +POx [Ox ]aq ) / ([At- ]aq +[Ox ]aq ) =( PA [At- ]aq +POx [At- ]aq eu) / ([At- ]aq + [At- ]aq eu ) = (PA + POxeu) / (1+eu).
Q14. Déterminer l’expression de P en fonction de PA et POx pour E = E°. Montrer que la dérivée de P par rapport à E pour la valeur E = E° s’écrit :
dP / dE = nF / (4RT) (POx-PA).
u = 0 ; eu = 1 ; PE=E°=½(PA+POx).
dP / dE = dP / du x du / dE.
u = nF / (RT) (E-E°) donc du / dE = nF / (RT).
P =(PA + POxeu) / (1+eu) donc dP / du = [ POxeu (1+eu) -(PA + POxeu)eu] / (1+eu)2=(POxeu -PAeu) / (1+eu)2.
Enfin pour E = E° : dP / du = 0,25 (POx-PA).
Conclusion ; dP / dE = nF / (4RT) (POx-PA).
Q15. Déterminer graphiquement les valeurs numériques de PA et POx
et les repérer sur une reproduction schématique de la courbe de la
figure 3. En déduire la valeur numérique du potentiel standard E° du
couple Ox/At–.
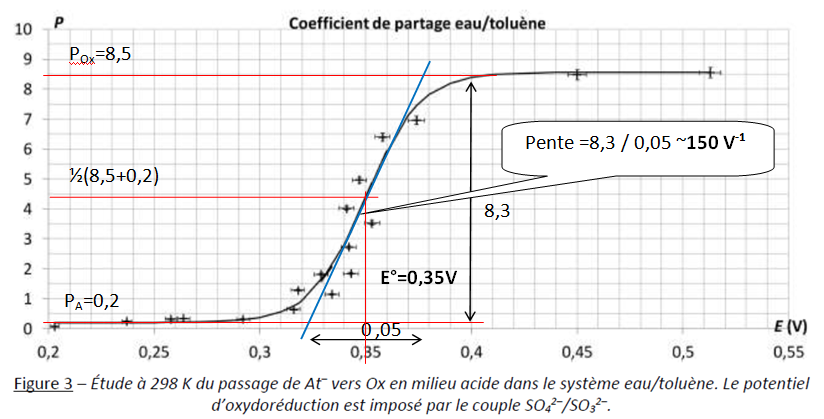
Q16. Montrer que le
nombre d’électrons échangés n vaut 2 en faisant apparaître sur le
schéma précédemment construit les éléments pertinents du raisonnement.
dP / dE = 140 V-1 pour E°.
dP / dE = nF / (4RT) (POx-PA) = n x 96500 x (8,5-0,2) / (4 x8,31 x298) ~80,9 n.
n = 150 / 80,9 =1,85 ~2.
Les résultats des calculs théoriques issus de modèles plus ou moins
élaborés ainsi que des mesures expérimentales sont regroupés dans le
tableau suivant :
|
Potentiel standard (V)
|
Couple
|
Calcul
|
Expérience
|
Cl2 aq / Cl-
|
1,47
|
1,396
|
| Br2 aq / Br- |
1,16
|
1,087
|
| I2 aq / I- |
0,72
|
0,621
|
| At2 aq / At- |
de 0,15 à 0,26
|
0,35
|
Q17.
Expliquer clairement, pourquoi les auteurs des recherches ont conclu
que la formule de l’espèce chimique de degré d’oxydation β en milieu
acide était At+.
Pour Cl, Br et I, les potentiels expérimentaux sont inférieurs à ceux calculés. Cela est faux pour l'astate.
L'espèce chimique de degré d'oxydation ß en milieu acide est donc At+et non At2.
Q18. Proposer une manipulation simple qui permettrait de confirmer le choix entre At2 et At+.
Soumettre l'espèce à un champ électrique :
Sans déplacement observé, elle ne porte pas de charge.
Déplacement observé, elle porte une charge électrique dont le signe est donné par le sens du déplacement.
|
...
|
....
|
Détermination de la formule de l’espèce chimique de degré d’oxydation g en milieu acide.
L’étude du potentiel du couple g/At+
a été réalisée de la même manière que précédemment, à l’aide de
constantes de partage sur une résine (équilibre solide/liquide au lieu
de liquide/liquide). Inconnue, la formule de l’espèce chimique de degré
d’oxydation 𝛾 est en premier lieu nommée AtOpr-2p où « r – 2p » représente la charge de l’espèce.
Comme pour l’étude précédente, les variations de la constante de
partage permettent de déterminer le nombre d’électrons échangés ainsi
que le potentiel du couple lorsque les concentrations en chacune des
espèces sont égales.
L’étude, réalisée à différents pH compris entre 0,0 et 2,0 a permis de
montrer que le nombre d’électrons échangés valait encore 2. La courbe
des potentiels obtenus est donnée.
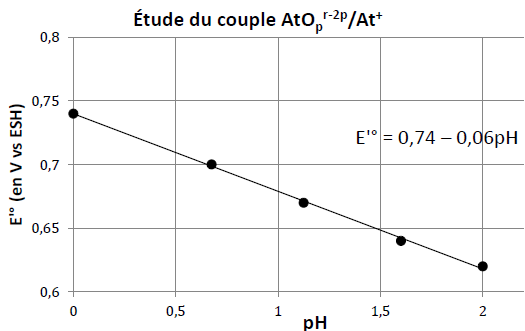
Q19. Expliquer comment les auteurs de l’étude ont pu attribuer la formule AtO+ à l’espèce chimique de degré d’oxydation g en milieu acide.
AtOpr-2p + 2 p H+ + 2e- = At+ + pH2O.
Formule de Nernst : E = E° +0,03 log ([AtOpr-2p][H+]2p / [At+])
E = E° -0,03 p pH +0,03 log ([AtOpr-2p] / [At+]).
Pour ([AtOpr-2p] = [At+], E = E° -0,03 p pH=0,74 -0,06 pH d'après le graphe.
Par suite p = 1 et AtOr-2 + 2 H+ + 2e- = At+ + H2O.
Conservation de la charge : r-2 = 1 soit r = 3.
AtO+ + 2 p H+ + 2e- = At+ + H2O.
Propriétés acido-basiques des espèces chimiques de degré d’oxydation g.
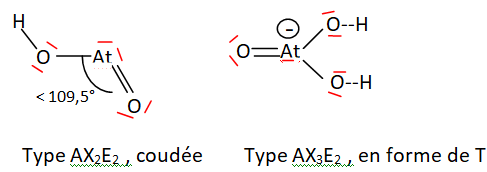
La détermination des formules des espèces chimiques de degré d’oxydation g en milieux neutre et basique a été réalisée de la même manière qu’en milieu acide. Les espèces [AtO(OH)] et [AtO(OH)2]– ont été mises en évidence.
Q21 On considère les espèces [AtO(OH)] et [AtO(OH)2]–.
En utilisant la théorie de la VSEPR, proposer une représentation
spatiale autour de l’atome d’astate pour chacune de ces deux espèces.
Q22. Des calculs
théoriques permettent de prédire l’angle O-At-O dans l’espèce [AtO(OH)]
: ils donnent 99,6°. Commenter cette valeur au regard de celle de
l’angle H-O-H (104,5°) dans la molécule d’eau.
La molécule d'eau est aussi du type AX2E2 ;
l'atome d'oxygène est plus petit et plus électronégatif que l'atome At.
Les doblets de liaisons sont plus localisés sur l'atome central et la
répulsion entre ces paires liantes sera plus grande.
Afin de comprendre la capacité de l’espèce AtO+ à réagir avec l’ion HO–
ainsi que la géométrie de l’espèce [AtO(OH)] formée, on cherche à
déterminer les orbitales moléculaires en interaction. Ne disposant pas
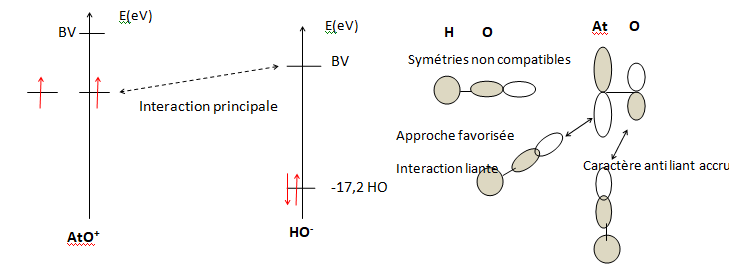
d’informations sur le diagramme d’orbitales moléculaires de AtO+, celui de ClO+ est pris comme modèle.
Q23. À partir du diagramme qualitatif d’orbitales moléculaires de ClO+ fourni, déterminer la configuration électronique de ClO+ et repérer ses orbitales frontalières (OF). Indiquer la signification des * dans les noms des orbitales concernées.
L'énergie
de l'orbitale 2 s de l'oxygène ( -33,9 eV) diffère beaucoup des autres
orbitales ( -17,2 et -13,6 eV). Sa participation sera donc écartée.
Les orbitales 1s et 2pz ont la même symétrie de révolution : elles permettent de former 2 orbitales moléculaires ( une liante et une antiliante)
Les orbitales 2px et 2py ne peuvent pas interéagir.
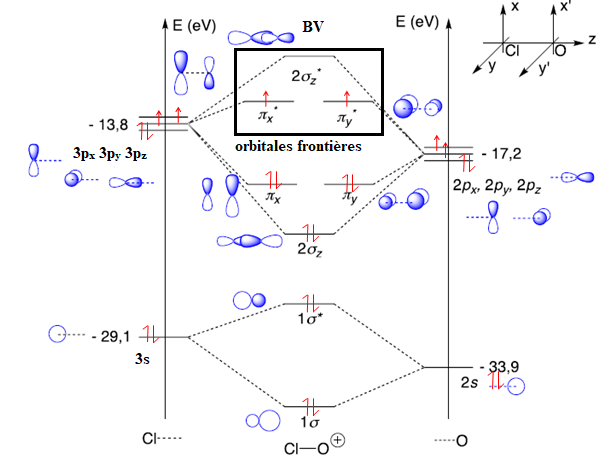
L'astérisque * signifie que l'orbitale est antiliante.
Q24. Etablir un diagramme qualitatif d’orbitales moléculaires de HO–. Déterminer la configuration électronique de HO–, et repérer les OF.
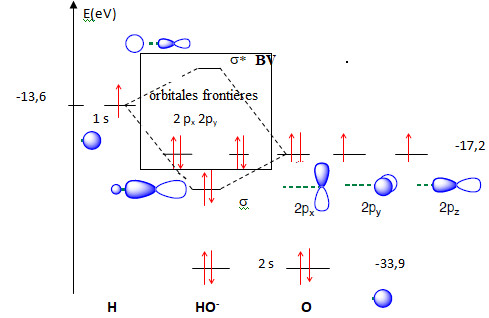
Nombre d'électrons pour HO- : 1 électron pôur H, 6 électrons pour O et un électron pour la charge : total 8.
Configuration électronique pour HO- : ns2 s2ny2nx2.
Q25. Positionner qualitativement les OF des deux fragments AtO+ et HO–.
En déduire les interactions à considérer lors de la formation de
l’espèce [AtO(OH)]. Montrer pourquoi l’approche selon un angle O-At-O
de 99,6° est bien favorisée par rapport à 180° ou 90°.
Acidité de l’espèce chimique AtO+.
On étudie les propriétés acido-basiques de l’espèce chimique AtO+ dont les valeurs des pKa sont données ( pKa1 = 2 ; pKa2 = 7,2).
.
Compte-tenu des particularités de l’astate, les concentrations des
solutions étudiées sont extrêmement faibles. Comprises entre 10–15 et 10–11 mol.L–1, ce ne sont pas des concentrations habituelles pour des calculs en chimie des solutions.
Q26. En supposant que l’on dispose d’une solution aqueuse d’AtO+ de concentration c = 1,0.10–3 mol.L–1, déterminer le coefficient de dissociation de AtO+.
Réaction entre l'acide le plus fort AtO+ et la base la plus forte H2O.
|
AtO+ |
+2H2O |
=AtO(OH)
|
+H3O+
|
initial
|
C
|
solvant
|
0
|
0
|
équilibre
|
C-xéq
|
xéq |
xéq |
Ka= xéq2 / (C-xéq) = 10-2.
xéq2 +10-2 xéq -10-5 =0.
Discriminant D =10-4+4 10-5 =1,4 10-4 ; solution positive : xéq =½ (-10-2+1,2 10-2) ~9,16 10-4 soit pH~3,0.
Coefficient de dissociation de AtO+ : xéq / C =9,16 10-4 / 10-3 = 0,916 (91,6 %).
L'acide AtO+ est très dissocié.
Q27.
Expliquer comment évolue le coefficient de dissociation d’une espèce
acide avec la dilution. Nommer la loi correspondante. Sans calcul,
évaluer alors le coefficient de dissociation pour une concentration c’
de l’ordre de 10–11 mol.L–1.
Loi de dilution d'Ostwald : par dilution, l'équilibre est déplacé vers la droite. Le coefficient de dissociation sera de 100 %.
Q28. Sans calcul mais en justifiant, évaluer la valeur du pH d’une solution aqueuse de AtO+ à la concentration c’.
Il faut tenir compte de l'autoprotolyse de l'eau qui apporte des ions H3O+. Celle-ci apporte majoritairement des ions H3O+. Donc le pH sera voisin de 7.
Q29. Commenter les stabilités de ces espèces en solution aqueuse.
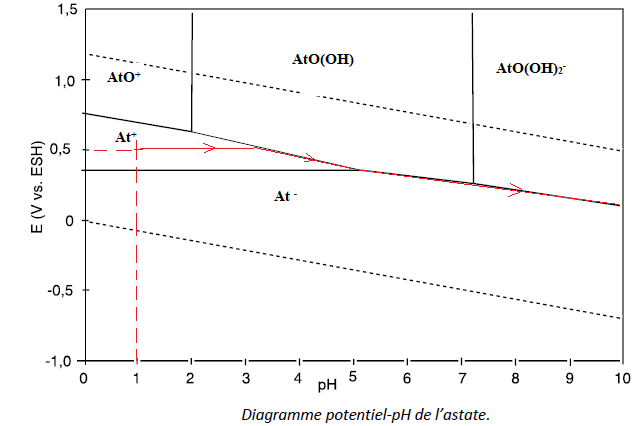
Toutes les espèces possèdent un domaine commun avec l'eau, elles sont donc toutes stables dans l'eau.
Q30. On considère une électrode de platine trempant dans une solution d’ions At+
à un pH = 1, soumise à un potentiel initial égal à 0,5 V. Une base est
ajoutée à la solution. Sur une représentation approximative à main
levée du diagramme, faire apparaître le point représentatif du système
au
début puis son évolution jusqu’à un pH aux environs de 10. Expliquer cette évolution.
Le point (pH=1 ; E = 0,5 V) se situe dans le domaine où At+ prédomine. En absence d'ajout d'oxydant, At+ n'est pas oxydé.
Le pH croît, ce point se déplace vers la droite et atteint la frontière At- / AtO(OH) puis la frontière At- / AtO(OH)2-.
On passe de At- au mélange At- ; AtO(OH), puis au mélange At- ; AtO(OH)2-.
Q31. Écrire l’équation de la réaction se produisant dans l’eau à partir de At+ comme seul réactif et pour un pH compris entre 5 et 7. Nommer ce type de réaction.
Entre pH=5 et pH = 7, At+ est à la fois oxydé en AtO(OH) et réduit en At- : réaction de dismutation.
At+ +2e- = At-.
At+ +2H2O = AtO(OH) + 3H+ +2e-.
2At+ +2H2O = AtO(OH) + 3H+ +At+.
|
|