Machine à
force de surface (SFA), mesure de force, concours agrégation interne
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Mesures de forces.
La
machine à force de surface (SFA) estreprésenté schématiquement sur la
figure ci-dessous. Elle permet de mesurer la force qui s’exerce entre
deux surfaces (en l’occurrence une sphère de rayon millimétrique et un
plan) entre lesquelles est
introduit un fluide tout en contrôlant la distance entre celles-ci, à
une fraction de nanomètre près. En mode dynamique,
la sphère est excitée, dans la direction normale au plan, par une
vibration sinusoïdale de petite amplitude (typiquement 1 nm) appliquée
au moyen d’une céramique piezoélectrique. Le plan est monté sur un
bilame élastique dont la déformation est mesurée grâce à un capteur
optique qui ne sera pas étudié dans ce problème. La force exercée par
le bilame sur le plan est simplement reliée à la déformation du bilame
multipliée par sa raideur. Le bilame constitue ainsi un capteur de
force. Le
déplacement relatif entre la sphère et le plan est, quant à lui, mesuré
par un capteur capacitif.
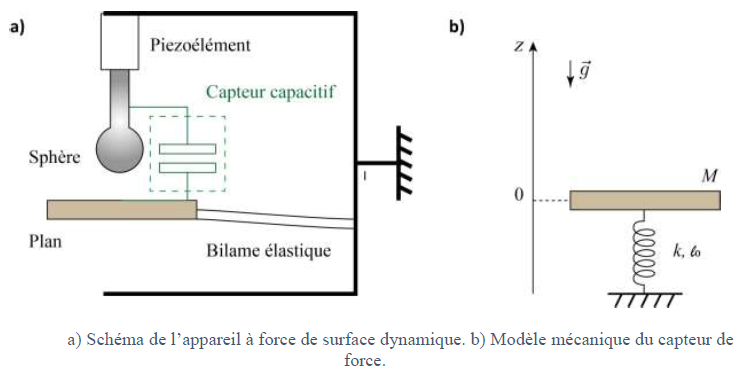
1. Mesure de forces.
On peut modéliser le bilame élastique qui sert de capteur de force par
un ressort de raideur 𝑘 et de longueur à vide l0
. On note M la masse du plan déposé sur le ressort susceptible de se
déplacer suivant un axe vertical O𝑧 orienté par le vecteur unitaire,
noté ez , dirigé vers le haut. Le point O (z=0) est choisi à
la position d’équilibre du plan quand la sphère n’exerce aucune force
sur le plan.
Le déplacement du plan est mesuré grâce à un dispositif optique qui
n’est pas étudié dans ce problème.
Dans cette partie, le capteur de force est étudié en l'absence de force
exercée par la sphère sur le plan.
1. Mécanique au
collège.
a. Indiquer deux
fausses conceptions initiales que l’on retrouve chez de nombreux élèves
en cycle 3 et début du cycle 4 concernant la notion de vitesse et la
notion de relativité des mouvements.
Force et vitesse sont toujours colinéaires. S'il n'y a pas de force,
alors la vitesse de l'objet est nulle.
Les objets ont un mouvement et une vitesse indépendamment du
référentiel.
Confusion entre temps et durée, entre position, vitesse et accélération.
b. Proposer, en une
vingtaine de lignes maximum, une séquence pédagogique pour faire
émerger une de ces deux conceptions initiales et y apporter une
réponse. On y intègrera une expérience de cours à préciser.
Etude du mouvement de plusieurs points sur une roue dans différents
référentiels.
Les élèves se répartissent par groupes de 3.
Cas n°1 : etude du mouvement du centre de la roue dans le référentiel
terrestre. (mouvement rectiligne uniforme)
Cas n°2 : étude du mouvement de la valve dans le référentiel terrestre.
( mouvement curviligne non uniforme )
Cas n°3. étude du mouvement du centre ( immobilité ) et de la valve (
mouvement circulaire uniforme) dans le référentiel du centre de la roue.
Tracé de la trajectoire : pointage + logiciel ou papier calque.
2. Rappeler ce
qu’est un référentiel. Définir « référentiel galiléen ».
Un référentiel est un objet de référence par rapport auquel on étudie
un solide en mouvement.
Le référentiel est galiléen si le barycentre d'un système fermé et
isolé se déplace avec un vecteur vitesse constant ( mouvement
rectiligne uniforme ).
3. En l’absence de
force exercée par la sphère sur le plan, identifier les forces qui
s’appliquent sur le système mécanique constitué par le plan. Pour un
plan de masse typique M = 30,0 g et un ressort de raideur typique k =
1,00 · 103 N.m-1, calculer la valeur de
l’enfoncement du ressort à l'équilibre.
Poids, verticale, vers le bas, valeur P =Mg.
Tension du ressort, verticale, vers le haut, valeur T = k |l-l0|.
A l'équilibre, ces deux forces se compensent :
Mg = k |léq-l0| ; |léq-l0 |= Mg / k =
0,0300 x9,81 / (1,00 103) =2,94
10-4 m.
4. Appliquer le
principe fondamental de la dynamique au système constitué par le plan
de masse M, en déduire l’équation différentielle du mouvement reliant
la position z du plan, à ses différentes dérivées temporelles z' et z".
Montrer que cette équation différentielle peut s’écrire sous la forme :
z"+ w02
z = 0
Exprimer la pulsation propre w0 en
fonction de k et M. À partir des dimensions de k et de M, justifier
l’homogénéité de cette relation.
Ecrire la seconde loi de Newton suivant l'axe Oz : -Mg +k( l0 -l) = Ma
= M z".
-Mg +k( l0 -léq +léq- l)
= M z".
Or -Mg + k( l0 -léq )= 0
; d'où : k( l -léq )= M z" soit -kz = M
z" ou z" +k / M z = 0.
w02 z=
k / M.
M s'exprime en kg et k en N m-1 soit kg m s-2 m-1 soit kg s-2 ; k
/ M s'exprime en s-2.
5. Exprimer la
solution générale de cette équation. Indiquer combien il faut de
conditions initiales pour la déterminer entièrement. On suppose qu’on
écarte le plan d’une quantité z0 et qu’on le lâche avec une
vitesse initiale nulle, établir alors l’équation horaire du mouvement.
z = A cos ( w0t + B).
A et B sont des constantes déterminées par 2 conditions initiales.
A t = 0; z0 =Acos (B) ; v (t)= z'(t) = -A w0 sin ( w0t + B).
v(t=0) = -A w0 sin B = 0 soit B = 2 k p.
Par suite z = z0 cos ( w0t ).
6. Pour déterminer
la valeur de la raideur k, une technique consiste à rajouter des
masselottes de masse m à la masse M. On observe que la pulsation propre
du système M+m est désormais w1.
Exprimer w1 en
fonction de k, M et m.
Sur la figure suivante, on représente les valeurs de 1/w12 en
fonction de m. Estimer un ordre de grandeur de la valeur de la raideur
k et de la valeur de la masse M correspondant à ces mesures.
w12 =k
/(M+m) soit 1/w12 =
(M+m) / k.
Le graphe est donc une droite de pente 1 / k et d'ordonnée à l'origine
M / k.
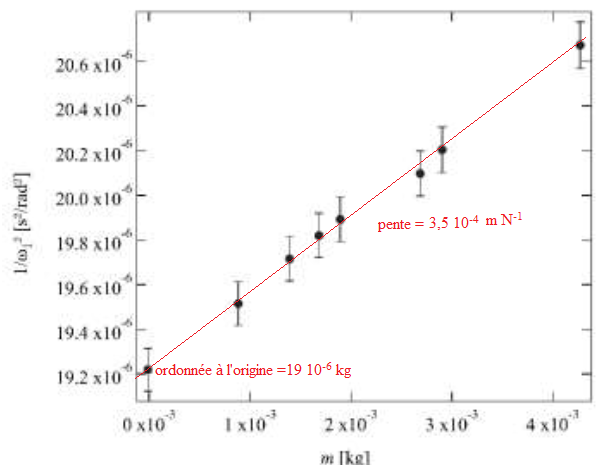
k = 1 /(3,5 10-4) =2,9 103 N/m.
M = 19 10-6 x2,9 103 =5,4 10-2 kg = 54
g.
|
...
|
....
|
7.
On modélise la dissipation dans cet oscillateur par une force de
frottement fluide proportionnelle à la vitesse du plan et de sens
contraire à la vitesse. ( |f |= a
M v. Donner la nouvelle équation différentielle du mouvement.
-Mg
+k( l0 -l) - a M z' = M z".
z"+ a z'+ w02 z
= 0.
Dans toute la suite du problème, on supposera
que cet amortissement est faible, de sorte que a << w0.
On définit le facteur de qualité Q par : Q =w0 / a >>
1.
Dans un premier temps, on s’intéresse aux oscillations libres de ce
système mécanique oscillant amorti, on montre que la solution approchée
de l’équation différentielle obtenue à la question 7 peut se mettre
sous la forme : 𝑧(𝑡) = 𝑧0 e−a𝑡/2 cos(w0 t + F).
8. La dissipation
d’énergie est traitée comme une perturbation par rapport au cas d’un
système non amorti. Compte tenu du choix de l’origine de l’axe Oz,
établir l’expression de la valeur moyenne temporelle de l’énergie
mécanique <E> du système non amorti en fonction de k et 𝑧0.
Energie mécanique = énergie potentielle élastique + énergie cinétique.
E = ½k z2 +½Mv2.
E = ½ k z20
cos2 ( w0t )+½M w02sin2 ( w0t )
avec M w02= k.
E = ½ k z20
cos2 ( w0t )+½k
z20sin2 ( w0t )=½k z20
= <E>
( énergie mécanique constante ).
9.
Montrer qu’au premier ordre en 1 / Q, l’énergie dissipée par frottement
pendant une période s’écrit
DE=2 p / Q<
E>.
En déduire une interprétation énergétique du facteur de qualité Q
dans cette limite de faible amortissement.
Energie mécanique dissipée par frottement sur une période DT = 2 p / w0 :
Efrot = - a
M z' z = - a M z2 ' DT .
<Efrot
> = -2 p/ w0 a M <z2
'> = -2 p/ w0 a k / w02<z2
'>.
z(t) = 𝑧0
e−a𝑡/2
cos(w0 t + F).
z '(t) = w0 z0e−a𝑡/2[-a/(2w0)cos(w0 t + F) - sin(w0 t + F)] ~ -w0 z0e−a𝑡/2 sin(w0 t + F).
<z2
'>= (w0 z0)2<e−a𝑡 sin2(w0 t + F)>
=½(w0 z0)2 e−a𝑡.
<Efrot
> =-2 p/ w0 a k / w02 ½(w0 z0)2 e−a𝑡= -2 p/ w0 a k ½ z02 e−a𝑡= -2 p/ Q k ½ z02 e−a𝑡= -2 p/
Q<E>
Facteur de qualité Q = 2p / DE <E>.
Le facteur de qualité est sans dimension ; il caractérise
l'amortissement de l'oscillateur.Plus Q est grand, plus l'amortissement
est faible.
On
s’intéresse maintenant au régime sinusoïdal forcé où le plan est soumis
à une force excitatrice supplémentaire que l’on note en représentation
complexe 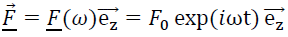 avec 𝐹0 > 0. avec 𝐹0 > 0.
Le régime transitoire n’est pas pris en compte dans cette description.
En pratique cette force est appliquée grâce à un petit aimant de masse
négligeable, collé sous le plan, placé en face d’une bobine que l’on
fait parcourir par un courant sinusoïdal. Ce système bobine-aimant
permet de déterminer la fonction de transfert du SFA.
10. Expliquer
comment le système bobine-aimant décrit ci-dessus permet
d’appliquer une force sinusoïdale sur le plan.
Une bobine parcourue par un courant sinusoïdal se comporte comme un
électroaimant. Un champ magnétique sinusoïdal est créé. Ce champ exerce
une force sinusoïdal sur l'aimant.
11. Expliciter la
propriété de l’équation du mouvement qui justifie
l’utilisation de la notation complexe.
L'équation du mouvement est linéaire.
12. Exprimer
l’amplitude complexe z(w) des oscillations en
fonction
de F0, M, w,
w0
et a.
z(t) = z(w) exp(iwt) ; z '(t) = iw z(w) exp(iwt) ; z "(t) = -w2 z(w) exp(iwt).
La seconde loi de Newton s'écrit : -Mg -k(z +Dl) -M a z' +F(t) = M z"
-k z -M a
z' +F(t) = M z"
En notation complexe : -k z -M a z' +F(t) = M z"
z(w) [-k -iMaw+Mw2]=-F0.
z(w)=F0 / M [1 /(k
/M +iaw-w2)]= F0
/ M [1 /(w02
+iaw-w2)].
13. On
définit la fonction de transfert complexe H(w) =k z(w) / F0. Préciser
l’expression du module |H(w)| et
de la phase F(w) (on fera attention à
séparer le
cas w < w0
et w
> w0)
de H(w).
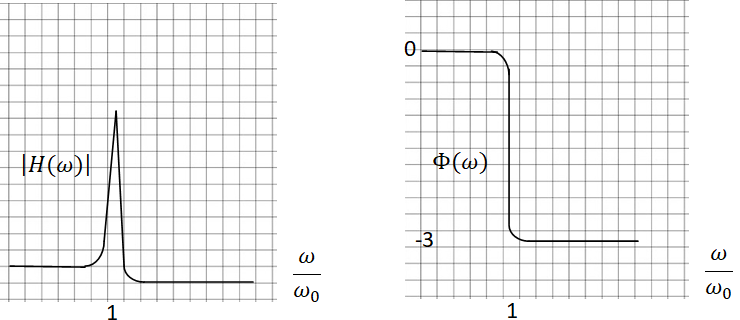
Calculer |H(0)|, |H(w0)|
et |H(+∞)|
Tracer l’allure de ces fonctions.
H(w) =w02 / (w02 +iaw-w2) .
|H(w)| =w02 / [(w02-w2)2 +a2w2 ]½.
F(w) = -arctan [aw / (w02-w2)]
pour w < w0.
F(w) = -arctan [aw / (w02-w2)] -p pour w > w0.
F(w0) = - p /2.
|H(0)| = 1 ; |H(w0)| =
Q ; |H(+∞)|
=0.
Tracés pour Q = 10.
14. Sur la figure suivante, les expérimentateurs ont choisi de
travailler en
fréquence plutôt qu’en pulsation et ont tracé le module |H(f)| de H(f) en fonction de la
fréquence f. Estimer l’ordre de grandeur du facteur de qualité à partir
de la courbe expérimentale de
la figure en s’appuyant
sur la question 13.
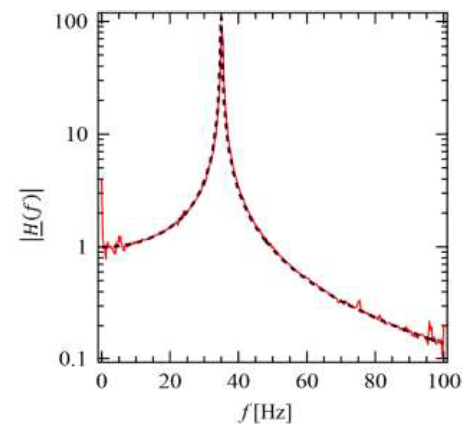
|H(w0)| =
Q = 100.
15.
Donner une valeur typique du facteur de qualité d’un diapason,
oscillateur mécanique très souvent utilisé en classe. Expliquer comment
on peut l’estimer avec un
chronomètre. Comparer au facteur de qualité du SFA.
Le facteur de qualité d'un diapason est de l'ordre de 1000, valeur bien
plus élevée que le facteur de qualité du SFA.
Frapper fortement un diapason et noté le temps au bout duquel
l'intensité sonore est divisée par 2. Après l'excitation, on entend le
son durant environ 3 s ; fréquence du diapason f = 440 Hz ; Q = 3 x440
= 1200.
16. Expliquer en
quoi la connaissance de la fonction de transfert
complexe est importante par rapport à la simple connaissance de la
raideur k ?
Pour mesurer des forces dépendantes du temps avec le SFA, il faut
connaître de manière précise la réponse en fréquence du capteur de
forces.
|
|