D�riv�es, convexit�, point d'inflexion, Oral concours Advance 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.


.
.
.. ..
......


...
D�riv�es.
  1. D�terminer les d�riv�es des fonctions suivantes d�finies par :
a. f(x) =ln(x2-2x+3) pour tout x r�el.
On pose u = x2-2x+3 ; u' = 2x-2.
f '(x) = u' / u = (2x-2) / (x2-2x+3)

b.g(x) = e-2x / x pour tout x de R*+.
On pose u = e-2x et v = x ; u' = -2e-2x ; v' = 1.
(u'v-v'u) / v2 = (-2x e-2x-e-2x)/ x2= -e-2x (2x+1) / x2.

 2. D�terminer les d�riv�es des fonctions suivantes d�finies sur R par :
a. f(x) = (2x2+1)�.
On pose u = 2x2+1 ; u' = 4x.
f(u) = u� ; f '(u) = 0,5 u-� u' ; f '(x) = 2x / (2x2+1)�.
b. g(x) = 2x ln(x2+1).
On pose u = 2x ; v = ln(x2+1) ; u' = 2 ; v' = 2x /(x2+1).
u'v+v'u = 2 ln(x2+1)+4x2 /(x2+1).

 3. D�terminer les d�riv�es des fonctions suivantes d�finies par :
a). f(x) = (x2+1) / (x2-3x-2) pour tout x de R - {1 ; 2}.
On pose u =x2+1 et v =x2-3x-2. u' = 2x ; v' = 2x-3.
(u'v-v'u) / v2 =[2x(x2-3x-2)-(2x-3)(x2+1)] / (x2-3x+2)2.
f '(x) = (2x3-6x2-4x-2x3-2x+3x2+3) / (x2-3x+2)2.
f '(x) = (-3x2-6x+3) / (x2-3x+2)2.

b. g(x) = (2x3-x+1)2020.
On pose u = 2x3-x+1 ; u' = 6x2-1.
g(u) = u2020 ; g'(u) = 2020 u' u2019 ; g '(x) = 2020(6x2-1) (2x3-x+1)2019.

 4. D�terminer les d�riv�es des fonctions suivantes d�finies sur R par :
a. f(x) = x e1/x +3(x2+1)�.
 x e1/x  : on pose u = x et v =e1/x  ; u' = 1 v' = -e1/x / x2.
u'v + v'u = e1/x -e1/x / x = e1/x (1-1 /x).
3(x2+1)� : on pose u = x2+1 ; u' = 2x ; � u' u-� = x (x2+1)-� .
f '(x) = e1/x (1-1 /x) +3x (x2+1)-� .
b. g(x) = (sin(x) +cos(x)20.
On pose u = (sin(x) +cos(x) ; u' = cos (x) - sin(x).
g ' =20 u' u19.
g'(x) = 20 (cos (x) - sin(x))(sin(x) +cos(x)19.

 5. D�terminer les d�riv�es des fonctions suivantes d�finies  par :
a. f(x) = e2x ln(2x+1) pour x > 0,5.
On pose u = e2x et v = ln(2x+1) ; u' = 2 e2x ; v' = 2 / (2x+1).
u'v+v'u = 2e2x ln(2x+1)+2e2x /(2x+1).
b. g(x) = (ln(x2+1)]18 pour x r�el.
On pose u = x2+1 ; u' = 2x.
w = ln(x2+1)  ; w' = 2x / (x2+1).
D�riv�e de w18 = 18 w17 w' = 18[ln(x2+1)]172x / (x2+1).

Convexit�.
6.  Soit la fonction d�finie sur R par f(x) = (x2+1) ex et C sa courbe repr�sentative.
a. Etudier les variations de f sur R.
b. Etudier la convexit� de f sur R et pr�ciser les �ventuels points d'inflexion pour la courbe C.
D�riv�e : on pose u = x2+1 et v = ex ; u' = 2x ; v' = ex.
f '(x) = u' v + v' u = 2xex +(x2+1)ex =(x2+2x+1)ex=(x+1)2ex >0. f(x) est croissante sur R.
D�riv�e seconde :
On pose u = x2+2x+1 et v = ex ; u' = 2x+2 ; v' = ex.
f "(x) = u' v + v' u = 2(x+1)ex +(x2+2x+1)ex =(x2+4x+3)ex.
f " a le signe de x2+4x+3 :
x2+4x+3=0 ; discriminant D =42-4 *3 = 4 = 22.
x1 = (-4 +2) / 2 = -1 ; x2 =(-4-2) / 2 = -3.

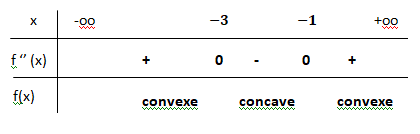
Au points d'abscisse x = -3 et x = -1, la d�riv�e seconde s'annule et change de signe. Ce sont deux points d'inflexion.

7. Soit la fonction d�finie sur R par f(x) = x2-4+ e-x et C sa courbe repr�sentative.
a. Etudier la convexit� de f sur R.
D�riv�e f ' =2x-e-x.
D�riv�e seconde  f "(x) = 2+e-x.
f "(x) est strictement positive sur R : f(x) est convexe sur R.
b. Soit a un r�el. D�terminer une �quation de la tangente � C au point d'abscisse a.
Coefficient directeur de la tangente : f '(a) = 2a-e-a.
Le point de coordonn�es (a ; f(a) = a2-4+e-a ) appartient � la tangente.
Equation de la tangente : y = f '(a) x + b.
a2-4+e-a =2a2-ae-a + b ; b = -a2-4+e-a +ae-a .
y = ( 2a-e-a)x -a2-4+e-a +ae-a .
c. D�duire l'�quation de la tangente � C au point d'abscisse 0.
a = 0 ; y = -x -3.
d. Montrer que pour tout r�el x : e-x+x2-4 > -x-3.
f est convexe sur R ; C se trouve toujours au dessus de ses tangentes.
En particulier en x = 0 : e-x+x2-4 > -x-3.


....
8. Soit f la fonction d�finie sur R par f(x) = x4-2x3-120x2+3 et C sa courbe repr�sentative.
a. Etudier la convexit� de f sur R et pr�ciser les �ventuels points d'inflexion pour la courbe C.
D�riv�e premi�re : f '(x) =4x3-6x2-240 x= 2x(.2x2-3x-120).
D�riv�e seconde : f ''(x) =12x2-12x-240 = 12(x2-x-20).
Erude de x2-x-20 =0
Discriminant D = 1+80 = 81=92.
Solutions x1 = (1+9) / 2 = 5 ; x2 = (1-9) / 2 = -4

Au points d'abscisse x = -4 et x =5, la d�riv�e seconde s'annule et change de signe. Ce sont deux points d'inflexion.
b. D�terminer l'�quation de la tangente � C au point d'abscisse 0.
Coefficient directeur de la tangente : f '(0) = 0.
Le point de coordonn�es (0 ; f(0) = 3) appartient � la tangente.
Equation de la tangente y = 3.
c. Montrer que pour tout r�el x appartenant � [-4 ; 5 ], x4-2x3-120x2+3 < 3.
f est concave sur[-4 ; 5 ] ; C se trouve  au dessous de ses tangentes sur cet intervalle.
 x4-2x3-120x2+3 < 3.

. Soit f la fonction d�finie sur ]0; +∞[ par f(x) = x + 1 /x et C sa courbe repr�sentative dans un rep�re orhogonal.
a. �tudier la convexit� de f sur R et pr�ciser les �ventuels points d’inflexion pour la courbe C.
D�riv�e premi�re : f '(x) = 1-1 / x2.
D�riv�e seconde f ''(x) = 2 / x3.
Sur ]0; +∞[, f ''(x) >0 et f(x) est convexe.
 b. D�terminer l’�quation de la tangente � C au point d’abscisse 1.
Coefficient directeur de la tangente : f '(1) = 0.
Le point de coordonn�es (0 ; f(1) = 2) appartient � la tangente.
Equation de la tangente y = 2.
 c. Montrer que pour tout r�el x appartenant � ]0; +∞[, x + 1/ x ≥ 2.
f est convexe sur ]0; +∞[ ; C se trouve  au dessus de ses tangentes sur cet intervalle.
x + 1/ x ≥ 2.

  
menu