Mathématiques, Bts opticien lunetier Métropole 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
EXERCICE 1
Un étudiant effectue son stage dans une boutique de lunetterie.
 PARTIE A - Probabilités conditionnelles.
Cette boutique est spécialisée dans les montures réalisées à partir de bois recyclé. Elle propose deux modèles de montures : - les montures SURF, réalisées avec le bois d’anciennes planches de surf;
- les montures TRADITION, réalisées avec le bois provenant d’un ébéniste.
 Un client souhaitant acheter des montures a le choix entre deux formules :
 -la formule PERSONNELLE : les montures sont confectionnées sur mesure;
-la formule IMMEDIAT : le client achète un modèle déjà confectionné.
 On dispose des informations suivantes :
 • 65 % des montures vendues sont des montures SURF. Parmi elles, 10 % ont été vendues selon la formule PERSONNELLE, les autres ont été vendues selon la formule IMMEDIAT.
• 35 % des montures vendues sont des montures TRADITION. Parmi elles, 15 % ont été vendues selon la formule PERSONNELLE, les autres ont été vendues selon la formule IMMEDIAT.
 On choisit au hasard une monture ayant été vendue. On définit les évènements :
S : il s’agit d’une monture SURF.
 E : il s’agit d’une monture ayant été vendue selon la formule PERSONNELLE.
1. Représenter la situation à l’aide d’un arbre pondéré.
2. Calculer la probabilité P(S ∩E).
3. Démontrer que P(E) = 0,1175.

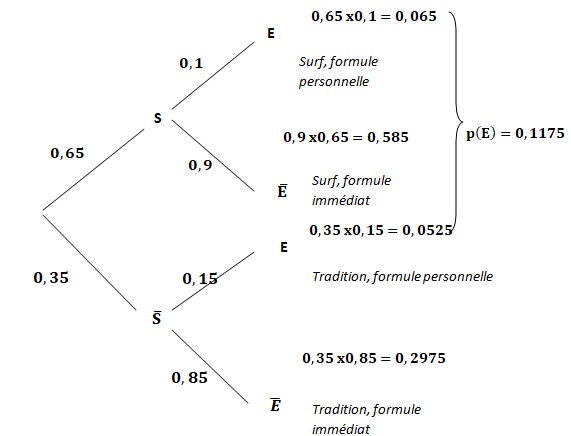4. La monture a été vendue selon la formule PERSONNELLE. Quelle est la probabilité qu’il s’agisse d’une monture SURF?
PE(S) = P(S n E) / P(E) = 0,065 / 0,1175 =0,553.

 Partie B  - Lois de probabilités
 Dans cette partie, on étudie les temps d’attente des clients selon les jours de la semaine. On a recueilli les observations ci-dessous.

 Description de la situation Loi de probabilité décrivant le temps d’attente exprimé en minutes Courbe correspondante
 Paramètres
Mardi, Jeudi
 Peu de clients. Peu d’attente. Loi exponentielle de paramètre l = 0,5. C1
 l = 0,5.
Mercredi, Vendredi
 Imprévisible. Un client peut attendre beaucoup, un peu, ou pas du tout Loi uniforme sur l’intervalle [a ; b]. C3
 a =0
b =8
Samedi
 Beaucoup de vendeurs, beaucoup de clients Loi normale de moyenne m et d’écart-type s = 1 minute. C2
 m=6.
s = 1 minute.
Dimanche, Lundi
 Boutique fermée.

On a représenté ci-dessous les représentations graphiques des densités des trois lois décrites dans le tableau ci-dessus.

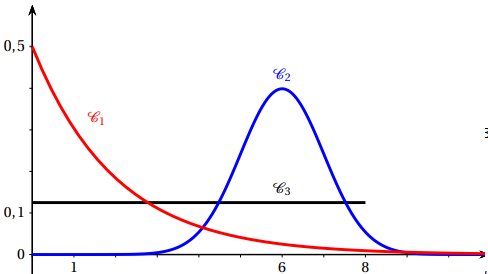1. Recopier  et compléter le tableau ci-dessus (colonnes 4 et 5 ).
2. Justifier que, le mardi, le temps d’attente moyen est égal à 2 minutes.
1 / l = 1 /0,5 = 2 minutes.
 3. Justifier que, le mercredi, la probabilité que le temps d’attente soit inférieur à 6 minutes est égale à 0,75.
6 /(8-0) = 6 /8 = 0,75.
4. Le samedi, quelle est la probabilité que le temps d’attente soit compris entre 4 et 8 minutes ? (Le résultat sera arrondi à 10−3 ).
P( temps d'attente < 4 )= 0,02275.
P( temps d'attente < 8 )= 0,9772.
P( 4 < temps d'attente < 8 )= 0,9772=0,02275=0,954.

 PARTIE C - Suites numériques
La boutique vend également des appareils auditifs. On constate que le nombre d’appareils vendus annuellement augmente de 12 % chaque année. On modélise cette évolution par une suite (un). Ainsi, selon cette modélisation, un représente le nombre d’appareils vendus durant l’année 2010+n. Par exemple, u7 représente le nombre d’appareils vendus durant l’année 2017.
 On suppose que l’on a u0 = 50. Tous les termes de la suite (un) seront arrondis à l’unité.
1. Calculer u1.
u1 = 1,12 u0 =1,12 x 50 =56.
2. Vérifier que, durant l’année 2012, le nombre d’appareils auditifs vendus est égal à 63.
u2 = 1,12 u1 =1,12 x 56=62,72 ( 63).
3. Justifier que la suite (un) est une suite géométrique dont on précisera la raison.
On passe d'un terme au suivant en le multipliant par 1,12.
Suite géométrique de raison q = 1,12, de premier terme u0 = 50.
un = 50 x1,12n.
 4. Résoudre, par la méthode de votre choix l’inéquation uN > 200. Interpréter le résultat dans le contexte de l’énoncé.
50 x1,12n > 200 ; 1,12n > 4.
n ln(1,12) > ln(4) ; n > ln(4) / ln(1,12) ; n >12,23  (13).
En 2010 +13 =2023, on vend plus de 200 appareils auditifs.

PARTIE D - Intervalle de confiance
 On souhaite estimer la proportion p de personnes intéressées par la commercialisation de lunettes connectées. On réalise un sondage auprès d’un échantillon de 200 clients. La clientèle est suffisamment importante pour assimiler cet échantillon à un tirage avec remise. Soit F la variable aléatoire qui à tout échantillon ainsi prélevé, associe la fréquence, dans cet échantillon, des clients intéressés par la commercialisation de lunettes connectées. On admet que F suit la loi normale de moyenne p inconnue dont l’écart-type est égal à [p(1-p) /200]½. Lors du sondage, 45 clients sur 200 ont dit être intéressés par la vente de lunettes connectées.
1. Donner une estimation ponctuelle f de la proportion inconnue p.
f =45 / 200 =0,225.
 2. Déterminer un intervalle de confiance centré sur f de la proportion p avec le niveau de confiance de 95 %. Arrondir les bornes de l’intervalle à 10−3 .
 f ± 2 s = f ±2 [f(1-f) /200]½= 0,225 ±0,059.
Intervalle de confiance : [0,225 -0,059 ; 0,225 +0,059] soit [0,166 ; 0,284].
3. La proportion p appartient-elle de façon certaine à cet intervalle ? Justifier.
Non, seulement  95 % des intervalles obtenus contiennent la proportion p.

...
....

 Exercice 2 10 points
Le glaucome est une maladie dégénérative du nerf optique qui entraîne une perte progressive de la vision. Cette maladie entraîne la dégénérescence des fibres nerveuses chargées de transmettre au cerveau les informations issues de la rétine.

PARTIE A - Statistique à deux variables.
La technique d’imagerie Tomographie en Cohérence Optique (OCT) permet de scanner la rétine et le nerf optique : en mesurant l’épaisseur des fibres du nerf optique on peut en déduire le nombre de fibres nerveuses optiques d’une personne. On a mesuré l’évolution du nombre N de fibres nerveuses optiques, en millier, en fonction du temps t, exprimé en mois, d’une personne atteinte d’un glaucome aigu. L’instant t = 0 représente le moment d’apparition du glaucome aigu. On obtient les résultats suivants :

1. À l’aide du graphique expliquer pourquoi un ajustement affine de N en t ne semble pas approprié.
Les points du graphique ne sont pas alignés.
 2. On décide de procéder à un changement de variable, en posant : z = ln(N −375). On obtient alors le tableau de valeurs suivant (les résultats ont été arrondis à 10−2 ).
temps t (mois)
 0
 1
 2
 3
 4
 6
 8
 12
 18
 24
z
 6,43
 6,31
 6,19
 6,06
 5,95
 5,70
 5,46
 5,00
 4,29
 3,53
a. Donner, à l’aide de la calculatrice, une équation de la droite de régression de z en t selon la méthode des moindres carrés, sous la forme : z = at +b, où a et b seront arrondis au millième.
z = -0,146 t +6,932.
 b. En déduire une expression de N en fonction de t de la forme : N = A e −0,12t +375, où A sera arrondi à l’unité.
ln(N-375) = -0,120 t +6,428.
N-375 = e-0,120t x e6,428 =619 e-0,120t .
N =619 e-0,120t +375.

PARTIE B - Résolution d’une équation différentielle.
 On considère une personne atteinte d’un glaucome aigu. y(t) désigne le nombre de milliers de fibres nerveuses optiques que possède cette personne t mois après l’apparition du glaucome. La fonction  y(t) modélise donc l’évolution du nombre de milliers de fibres nerveuses optiques au cours du temps. On admet que y est définie et dérivable sur [ 0 ; +∞[ et on note y ′ sa dérivée. On admet que la fonction y est solution de l’équation différentielle (E).
(E) : 2y ′ +0,24y = 90
1. Déterminer les solutions de l’équation différentielle : (E0) : 2y ′ +0,24y = 0

y' +0,12 y = 0 ; y(t) = Ae-0,12 t avec A une constante.
2. a. Soit g la fonction définie sur [ 0 ; +∞[ par g(t) = 375. Vérifier que la fonction g est une solution de (E).
g' = 0 ; repport dans (E) : 0,24 x375 =90 est bien vérifiée.
 b. En déduire les solutions de l’équation différentielle (E).
f(t) = Ae-0,12 t +375.
3. On sait que, à l’instant t = 0, le nombre de fibres nerveuses de la personne est de 994 milliers de fibres. Déterminer alors la solution y vérifiant cette condition initiale.
994 = A +375 ; A = 619.
f(t) = 6194e-0,12 t +375.

PARTIE C- Étude de fonction
On considère la fonction f définie sur [ 0 ; +∞[ par : f (t) = 375+619 e −0,12t . On suppose que l’évolution du nombre de fibres nerveuses optiques de la personne atteinte d’un glaucome peut être modélisée par la fonction f où f (t) représente le nombre de milliers de fibres nerveuses optiques t mois après l’apparition du glaucome. On admet que f est une fonction dérivable sur [ 0 ; +∞[ et on note f ′ sa fonction dérivée. On désigne par C la courbe représentative de la fonction f dans un repère orthogonal.
1. Démontrer que, pour tout réel t de l’intervalle [ 0 ; +∞[ , on a : f ′ (t) = −74,28 e −0,12t.
f '(t) = 619 x(-0,12) e-0,12t =−74,28 e −0,12t.
2. En déduire le sens de variation de la fonction f sur [ 0 ; +∞[ .
e −0,12t est positif ; f '(t) est strictement négative et f(t) est strictement décroissante.
 3. Déterminer la limite de la fonction f en +∞. Interpréter graphiquement.
e −0,12t tend vers zéro et f(t) tend vers zéro.
La droite d'équation y=0 est asymptote à la courbe représentant f(t).
4. QCM On admet qu’un développement limité à l’ordre 2 de la fonction f au voisinage de 0 est donné par : f (t) = 994−74,28t +4,4568t 2 + t 2 ε(t) avec lim t→0 ε(t) = 0.
Une équation de la tangente T à la courbe C au point d’abscisse 0 est :
y = −74,28t +4,4568t 2.
 y = 994−74,28t.
 y = 74,28t −994.
Coefficient directeur de cette tangente en t = 0 : f '(0) = -74,28.
Le point de coordonnées 0 ; f(0) = 994 appartient à cette tangente.
Equation de la tangente : y = -74,28 t +b.
994 = 0 +b ; b = 994.
y = -74,28 t +994.

  
menu