Mathématiques,
Bts groupe B1 Métropole
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1 : un problème de routage 5 points
Un chariot d’une fête foraine est propulsé à une vitesse de 20 m.s−1
sur un axe horizontal,
puis il est ralenti par un système de freinage.
On s’intéresse à la vitesse du chariot durant le freinage.
On note f (t) la vitesse du chariot à l’instant t.
f (t) est exprimé en mètre par seconde, et t est exprimé en seconde.
L’instant t = 0 correspond à l’instant où le chariot commence à être pris en charge par le
système de freinage. On a donc f (0) = 20.
On suppose que f est une fonction dérivable sur [0 ; +∞[ et on note f
′
sa fonction dérivée.
Les trois parties peuvent être traitées de façon indépendante.
Partie A - Résolution d’une équation différentielle.
On admet que la fonction f est solution de l’équation différentielle :
(E) : y
′ +0,8y = 4,
où y est une fonction inconnue et où y
′
est la fonction dérivée de y.
1. a. Résoudre l’équation différentielle (E0) : y
′ +0,8y = 0.
f(t) =A e-0,8t. A est une constante.
b. Soit g la fonction définie sur [0 ; +∞[ par g(t) = 5.
Vérifier que la fonction g est solution de l’équation différentielle (E).
g'(t) = 0, repport dans (E) : 0+0,8 x5 = 4 est bien vbérifié.
c. En déduire l’ensemble des solutions de l’équation différentielle (E).
f(t) = Ae-0,8t +5.
2. On rappelle que f (0) = 20.
Déterminer la solution f de l’équation (E) qui vérifie la condition initiale : f (0) = 20.
20 = A+5 ; A =15.
f(t) = 15e-0,8t +5.
Partie B - Étude de la fonction f
On admet que la fonction f est définie pour tout t appartenant à [0 ; +∞[ par :
f (t) = 15e−0,8t +5.
Sa courbe représentative C dans un repère orthogonal est donnée ci-dessous.
1. a. Démontrer que la limite de f(t) en plus l'infini est
f (t) = 5.
En plus l'infini, e−0,8t est nul et f(t) tend vers 5.
b. En déduire que la courbe C admet une asymptote dont on donnera une équation.
La droite d'équation y = 5 est asymptote à la courbe représentant f(t).
2. On admet que, pour tout réel t appartenant à [0 ; +∞[ on a :
f
′
(t) = −12e−0,8t
.
Dresser le tableau de variation de f sur [0 ; +∞[.
e−0,8t >0, f '(t) est strictement négative et f(t) est strictement décroissante.
3. Le système de freinage permet-il au chariot de s’arrêter ?
Non, la vitesse finale tend vers 5 m /s.
4. Soit F la fonction définie sur [0 ; +∞[ par F(t) = −18,75e−0,8t +5t.
a. Vérifier que la fonction F est une primitive de la fonction f sur [0 ; +∞[.
On dérive F : -18,75 x(-0,8) e−0,8t +5 =15e−0,8t +5 =f(t).
b. On admet que la distance d, exprimée en mètre, parcourue par le chariot entre
les instants t0 et t1 est donnée par :
d = F(t1)-F(t0).
Calculer la valeur exacte de la distance parcourue par le chariot entre l’instant
t0 = 0 et t1 = 1. Donner une valeur arrondie au centimètre.
F(1) =-18,75 e-0,8 +5.
F(0) = -18,75.
d = -18,75 e-0,8 +5+18,75 =23,75 -18,75e-0,8 ~15,33 m.
Partie C – Étude locale
On rappelle que l’on étudie la fonction f définie sur [0 ; +∞[ par :
f (t) = 15e−0,8t +5.
On rappelle que sa courbe représentative C est reproduite au début de la partie B.
Un logiciel de calcul formel affiche la partie régulière du développement limité à l’ordre 2 de
la la fonction f au voisinage de 0 soit 20 -12 t+24 / 5t2+t2e(t) avec e(t) tendant vers zéro quant t tend vers zéro.
Donner une équation de la tangente T à la courbe C au point d’abscisse 0.
y = -12 t +20.
|
...
|
....
|
Exercice 2 10 points
Une usine fabrique des tubes fluorescents. Des tests de conformité permettent de vérifier si
les tubes présentent un défaut.
Les trois parties peuvent être traitées de façon indépendante
Partie A - Probabilités conditionnelles
L’entreprise possède deux ateliers de production des tubes : atelier 1 et atelier 2.
• L’atelier 1 produit 30 % des tubes.
◦ Parmi eux, 1,5 % présentent un défaut.
• L’atelier 2 produit 70 % des tubes.
◦ Parmi eux, 2,5 % présentent un défaut.
On prélève au hasard un tube parmi la production totale de l’usine. On définit les évènements suivants :
• A1 : « le tube provient de l’atelier 1 »;
• A2 : « le tube provient de l’atelier 2 »;
• D : « le tube présente un défaut ».
1. Réaliser un arbre pondéré décrivant la situation.
2. Calculer la probabilité P (A1 ∩D).
3. Montrer que P(D) = 0,022.
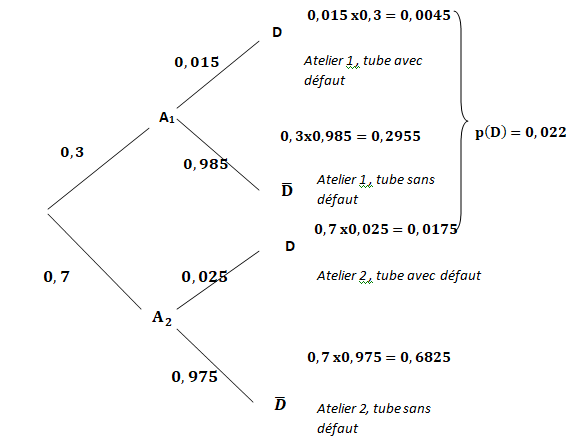
4. On sait que le tube ne présente pas de défaut.
Quelle est la probabilité qu’il provienne de l’atelier 2 ?
P non D (A2)=P(non D n A2) / P(non D)=0,6825 / (1-0,022)=0,698.
Partie B - Durée de vie des tubes fluorescents
On considère la variable aléatoire T qui, à tout tube fluorescent prélevé au hasard dans le
stock, associe sa durée de bon fonctionnement en heure.
On suppose que T suit une loi exponentielle de paramètre l = 0,0001.
1. Déterminer l’espérance E(T ) et interpréter le résultat dans le contexte de l’énoncé.
E(T) = 1 /l = 10 000 heures.
La durée de vie moyenne est de 10 000 heures.
2. Calculer la probabilité, arrondie à 10−2
, que la durée de bon fonctionnement du tube
fluorescent prélevé soit inférieure à 8 000 heures.
P(T < 8000) = 1-exp(-0,0001 x8000) = 1-e-0,8 =1-0,45= 0,55..
3. Calculer la probabilité, arrondie à 10−2
, que la durée de bon fonctionnement du tube
fluorescent prélevé soit supérieure à 10 000 heures.
P(T > 10 000 )=exp(-0,0001 x 10 000 ) =e-1 =0,37.
Partie C - Intervalle de confiance
La fixation des tubes fluorescents se fait à l’aide de rivets produits
dans une usine.
On cherche la proportion p de rivets conformes parmi l’ensemble de la
production.
Pour cela, on prélève au hasard dans la production un échantillon de 1
000 rivets. Ce prélèvement peut être assimilé à un tirage au sort avec
remise.
On constate que, sur les 1 000 rivets prélevés, 975 d’entre eux sont
conformes.
1. Donner une estimation ponctuelle f de la proportion inconnue p.
f = 975 / 1000 = 0,975.
2. Soit F la variable aléatoire qui, à tout échantillon de 1 000 rivets ainsi prélevé, associe
la fréquence, dans cet échantillon, des rivets conformes.
Déterminer un intervalle de confiance centré sur f de la proportion p au niveau confiance
de 95 %.
Arrondir les bornes de l’intervalle à 10−3 près
1,96 [p(1-p) / n]½ = 1,96 [0,975 x0,025 /1000]½ =0,00968.
Intervalle de confiance [0,975 -0,00968 ; 0,975 +0,00968) soit [0,965 ; 0,985]
|
|