Etude d'un
gymnase rénové, acoustique, transferts thermiques, polychlorure de
vinyle, BTS Batiment
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
A. Étude thermique du gymnase rénové (8 points)
Le but de cet exercice est d’analyser l’isolation thermique du gymnase rénové, d’une surface totale au sol de 1 400 m 2.
Nous prendrons en compte dans notre étude les éléments d’architecture suivants :
la toiture ;
les parois extérieures constituées de murs maçonnés en soubassement et d’une surface vitrée en polycarbonate ;
les portes-fenêtres à double vitrage.
L’ensemble des données liées aux éléments de structure du gymnase est recensé dans le tableau ci-dessous.
Elément
|
composition
|
l(W m-1K-1)
|
Rth pour 1 m2
(m2K W-1)
|
coef transmission
thermique U(Wm-2K-1)
|
épaisseur e(cm)
|
Surface totale S m2
|
toit
|
laine de verre
|
0,034
|
8,8
|
|
30
|
1400
|
profils acier
|
|
négligeable
|
|
|
Parois
|
murs
|
béton |
|
1,4
|
|
20
|
738
|
| laine de verre |
|
4,7
|
|
1,6
|
| bardage bois |
0,012
|
|
|
2,0
|
Surface vitrée
|
|
|
|
1,1
|
3,2
|
252
|
Portes-fenètres double vitrage
|
|
0,48
|
|
|
12
|
Pour les
parois verticales, il faut tenir compte de la convection et prendre en
compte les résistances superficielles intérieures et extérieures par
convection suivantes : r si = 0,11 m 2 K W -1 et r se = 0,06 m2 K W-1 pour 1 m².
La température de confort à l’intérieur du gymnase est de qint = 18°C.
La température moyenne à l’extérieur pendant les périodes d’utilisation du chauffage est de qext = 4,0°C.
La durée annuelle d’utilisation du chauffage est estimée à 150 jours ;
la durée journalière d’utilisation du chauffage est estimée à 10 h
chaque jour de la semaine. I. Les transferts thermiques.
1 - Donner le sens spontané des transferts thermiques à travers les parois, entre l’intérieur du gymnase et l’extérieur.
Les transferts thermiques s'effectuent du corps chaud ( intérieur du gymnase) vers le corps froid ( l'extérieur).
2 - Citer la grandeur physique qui représente le transfert thermique par unité de temps à travers une paroi. Donner son unité.
Le flux thermique surfacique exprimé en W m -2.
3 - Citer la
grandeur physique permettant de caractériser la capacité d’une paroi à
s’opposer au transfert thermique. Donner son unité.
La résistance thermique Rth pour 1 m2 (m2K W-1)
II. Isolation Thermique.
À l’aide des données du tableau :
4 - Retrouver par le calcul la valeur de la résistance thermique pour 1 m² du toit : R toit = 8,8 m2K W-1.
e / l = 0,30 / 0,034= 8,8 m2K W-1.
5 - Donner l’expression littérale du flux thermique surfacique Ftoit transféré à travers la toiture en fonction de la résistance thermique pour 1 m² du toit R toit, de la température intérieure qint et de la température extérieure qext. Calculer sa valeur.
Ftoit = (qint - qext) / Rtoit=(18-4) / 8,8=1,59 W m-2.
6 - Vérifier que le flux thermique transféré à travers la surface totale de la toiture est 2,2 kW.
Ftoit S = 1,59 x1400 ~2,23 103 W ~ 2,2 kW.
7 - Vérifier par le calcul la valeur de la résistance thermique des murs maçonnés, en tenant compte de la convection : R murs = 7,9 m2K W-1.
Rth béton + RTh laine de verre +ebardage / l bardage + rsi + rse=1,4 +4,7 +0,02 /0,012 +0,11 +0,06 =7,9 m2K W-1.
8 - Vérifier que le flux thermique transféré à travers la surface totale des murs maçonnés est 1,3 kW.
Fmurs = (qint - qext) / Rmur=(18-4) / 7,9=1,77 W m-2.
Fmurs Smurs =1,77 x 738 ~1,31 103 W ~1,3 kW.
Le flux thermique transféré à travers la surface vitrée en
polycarbonate est 3,9 kW ; celui transféré à travers les
portes-fenêtres à double vitrage est 0,26 kW.
9 - Montrer que la valeur du flux total transféré à travers toutes les parois du bâtiment est 7,7 kW.
2,2 +1,3 +3,9 +0,26~ 7,7 kW.
10 - Déterminer
l’énergie totale perdue par le bâtiment, en mégawattheures, pendant la
durée annuelle d’utilisation du chauffage de ce gymnase (1 M = 10 3 k).
Durée = 150 x10 = 1500 heures.
Energie perdue = 7,7 x1500 =1,16 10 4 kJ = 11,6 MJ ~12 MJ.
L’énergie nécessaire au chauffage du bâtiment avant rénovation était de 45 MWh.
11 - Déterminer la valeur du rapport entre consommée pour le chauffage avant et après rénovation. Commenter.
12 / 45 ~0,27.
L'isolation a permis de diviser par 3 l'énergie consommée par le chauffage.
|
...
|
....
|
B. Rénovation acoustique du gymnase (6 points)
Après une première période d’utilisation du gymnase qui a montré
un confort acoustique insuffisant, il a été décidé de rajouter des
panneaux suspendus isolants.
Le confort acoustique d’une salle est directement lié au temps de
réverbération acoustique TR, défini comme la durée nécessaire pour que
le niveau sonore, N en dB, diminue de 60 dB après l’arrêt de l’émission
de la source sonore.
On peut le calculer par la formule de Sabine : TR = 0,16 V/A
TR est le temps de réverbération acoustique (en s) ;
V est le volume du local (en m3) ;
A est l’aire d’absorption équivalente (en m2) définie par : A = Sai × Si, chaque surface Si étant affectée d’un coefficient d’absorption αi.
Pour toute la partie B, on considère l’enceinte du gymnase comme un
parallélépipède rectangle de dimensions intérieures 45 m × 30 m × 8 m.
Avant les travaux d’isolation acoustique dans le gymnase, on a procédé
à une détermination expérimentale de ce temps de réverbération,
illustrée par la courbe suivante.
12 - Déterminer le
temps de réverbération avant isolation acoustique du gymnase, en
précisant sur la courbe la construction graphique permettant cette
détermination.
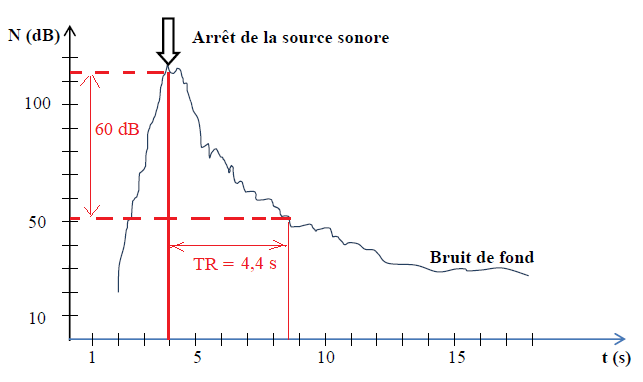
13 - À partir du
temps de réverbération mesuré, vérifier que la valeur de l’aire
d’absorption équivalente A du gymnase avant travaux était environ égale
à 4.102 m2.
Volume du gymnase = 45 x30 x8=10 800 m3.
A = 0,16 V / TR =0,16 x10 800 /4,4 ~ 4.102 m2.
14 -
Les travaux de rénovation acoustique ont pour objectif de réduire le
temps de réverbération. Indiquer comment on doit faire varier la
surface d’absorption équivalente A. Expliquer l’intérêt pour la
compréhension de la parole (dite aussi « intelligibilité de la parole
»).
La surface d'absorption équivalente doit augmenter.
Pour diminuer le temps de réverbération du gymnase, des panneaux suspendus sont installés.
Un temps de réverbération court permet à la personne qui écoute
d'entendre et de comprendre correctement le premier mot, le son
en émanant disparaît avant l'arrivée du mot suivant.
Données relatives aux panneaux isolants suspendus.
Coefficient d'absorption moyen : a = 0,80 ; surface : 670 m2.
15 - Calculer la nouvelle surface d’absorption équivalente A’ après les travaux de rénovation.
A' =A + 670 x 0,8 =936 m2.
16 - En déduire la nouvelle valeur du temps de réverbération. Commenter
TR' = 0,16 V / A' = 0,16 x10800 / 936=1,8 s.
Le confort acoustique est bien ammélioré.
Étude du revêtement de sol (6 points)
Le nouveau revêtement de sol du gymnase est
constitué d’un revêtement de surface en polychlorure de vinyle (noté A
sur le schéma) associé à un « support à déformation surfacique » (noté
B sur le schéma) reposant sur un film en polyéthylène (noté 6 sur le
schéma).

Ce nouveau revêtement de sol est donc composé de plusieurs matières
plastiques : le polychlorure de vinyle (PVC), le polyéthylène (PE) et
le polyuréthane (PU).
Quelques données :
Masse molaire atomique : M(C) = 12,0 g.mol-1 ; M(H) = 1,0 g.mol-1 ; M(Cl) = 35,5 g.mol-1.
Masse volumique moyenne du PVC à 25 °C : r = 1 300 kg m-3.
Conversion énergétique : 1 kWh = 3,6.106 J.
17 - Recopier et compléter les équations des réactions modélisant les polymérisations du polyéthylène PE et du PVC ci-dessous.
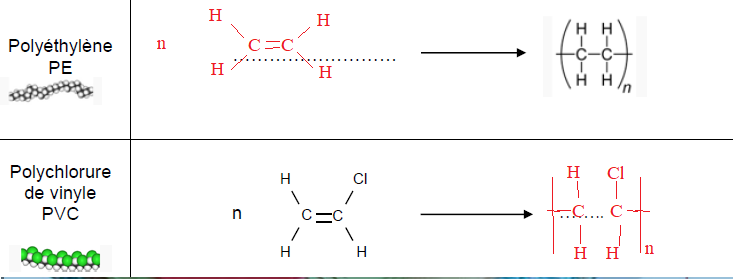
18 - Indiquer si les polymérisations du PE et du PVC sont des polyadditions ou des polycondensations. Justifier.
Polyaddition : addition de molécules différentes sans élimination de petites molécules comme dans les polycondensations.
19 - Définir l’indice n dans les formules des polymères.
n : nombre d'unités de monomère constituant le polymère.
20 - Calculer la masse molaire moléculaire du chlorure de vinyle CH2=CHCl, le monomère du PVC.
2 x12 + 3 +35,5 =62,5 g / mol.
21 - L’indice n du PVC étudié vaut en moyenne 1 500. Montrer que sa masse molaire moléculaire est égale à environ 94 kg.mol-1.
1500 x 62,5 =93 750 g ~94 kg / mol.
Le sol du gymnase est composé de plusieurs couches de différents
matériaux. Celle du PVC a une épaisseur de 2,2 mm. Le sol du gymnase a
pour dimension 45 × 30 m.
22 - Déterminer la masse de PVC utilisée pour couvrir le sol du gymnase.
Volume du PVC : V = 45 x 30 x2,2 10-3 =2,97 m3.
Masse volumique moyenne du PVC à 25 °C : r = 1 300 kg m-3.
Masse =1300 x2,97 ~3,86 103 kg.
23 - En déduire la quantité de matière en moles de PVC correspondant à cette masse.
3,86 103 / 94 ~ 41 mol.
La réflexion environnementale autour des économies d’énergie introduit la notion d’« énergie grise ».
24 - Définir ce qu’on appelle « l’énergie grise » d’un matériau.
Energie nécessaire à la fabrication, au transport et à l’élimination des matériaux.
On estime « l’énergie grise » du PVC à 5,9.103 MJ mol-1.
25 - Déterminer « l’énergie grise » en kWh par m3 du PVC utilisé sur le sol du gymnase.
5,9 103 x 41 =2,42 105 MJ.
1 kWh = 3,6.106 J = 3,6 MJ.
2,42 105 / 3,6 =6,7 104 kWh.
6,7 104 / 2,97 ~2,26 104 kWh m-3.
On fournit des données sur les « énergies grises » estimées de quelques matériaux.
Polyéthylène : 28 000 à 32 000 kWh m-3.
PVC : 21 000 à 27 000 kWh m-3.
Mousse polyuréthane :1 000 kWh m-3.
Bois (parquet) :50 à 1 000 kWh m-3.
26 -
En comparant les données, commenter, selon ce critère, le choix d’un
revêtement de sol à base de polymères par rapport à un parquet en bois
utilisé également dans certains gymnases.
27 - Citer deux
avantages des revêtements de sol à base de polymères par rapport au
parquet en bois qui expliquent leur utilisation dans certains gymnases.
Confort thermique et acoustique du revêtement à base de polymère, malgré une énergie grise très supérieure à celle du bois..
|
|


