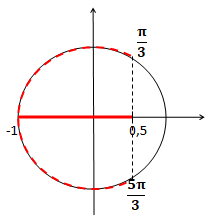
Mathématiques, technicien supérieur de l'aviation 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Question 1. Pour x appartenant à [0 ; 2p[, l'ensemble des solutions de l'inéquation cos(x) < -cos(2x) est : cos(x) +cos(2x) < 0 ; cos (2x) = 2cos2(x) -1. 2cos2(x) +cos(x) -1 < 0. On pose X =  cos (x) avec -1 < X < 1. Solutions de 2X2 +X-1 =0 ; discriminant D =1+8 =9=32. Solutions : X1 =(-1+3) / 4=0,5 et X2 =(-1-3) / 4 =-1. Solutions de 2X2 +X-1 < 0 : X, donc cos(x) appartient à [-1 ; 0,5]. cos (x) = -1 conduit à x = ± p ; cos (x) = 0,5 conduit à x = ±p/3. Réponse C :  x appartient à [p / 3 ;5 p/ 3 ]. Question 2. La solution de l'équation différentielle (E) 15 y' +24 y = 12 avec y(5 /4) = 2 est la fonction : Solution générale de 15 y'+24 y=0 : f(x) = A exp(-24 /15 x) = A exp(-8x / 5) avec A une constante. Solution particulière de (E) : y = 0,5. Solution générale de (E) : f(x) =A exp(-8x /5) +0,5. Or f(5 /4) =2=A exp(-10 /5 )+0,5 ; A =1,5 exp(2). f(x) =1,5 exp(2) exp(-8x /5) +0,5 =1,5 exp(-8x /5+2) +0,5. Question 3. Dans un repère orthonormé, nous considérons un hexagone régulier ABCDEF de centre O, dont les côtés ont pour mesure de longueur 1. 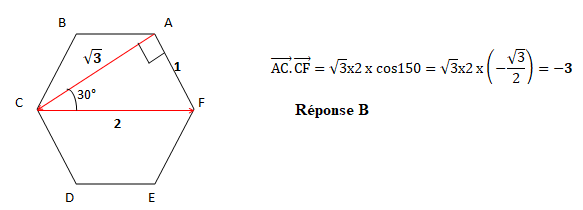Le produit scalaire suivant est égal à : Question 4. Soit une fonction g définie sur l’intervalle ]−∞; 0] ; sa courbe représentative dans un repère du plan admet-elle un asymptote. 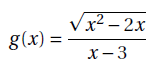Sur l’intervalle ]−∞; 0] : - le dénominateur n'est pas nul ; x2-2x =x(x-2) > 0  soit x = 0. 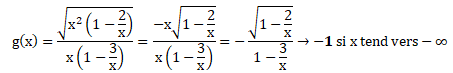La droite d'équation y = -1 est asymptote à la courbe. Réponse A. . Question 5. 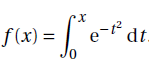Soit la fonction f définie sur l’ensemble des nombres réels par : La fonction f ′′, dérivée seconde de f sur l’ensemble des nombres réels, est définie par :  f '(x) = exp(-x2) ;  f "(x) = -2x exp(-x2). Réponse C. Question 6. On considère deux suites (un) et (un) définies sur l’ensemble des nombres entiers naturels : A. Si un tend vers plus l'infini et si vn tend vers moins l'infini, alors un + vn tend vers zéro. Faux, la forme un + vn est indéterminée. B. Si (un) converge vers un nombre réel non nul et si  vn tend vers moins l'infini, alors la suite (un ×vn) ne converge pas vers une limite finie. Vrai. C. Si (un) converge vers un nombre réel non nul et si vn tend zéro, alors la suite (un / vn ) admet +∞ou −∞comme limite. Vrai. D. Si (un) et (vn) convergent alors la suite (un / vn ) converge vers une limite finie. Faux. La limite de (vn) ne doit pas être nulle. Question 7. Dans un repère de l’espace, on considère les trois points : A(1; 2; 3), B(−1 ; 5 ; 4), C(−1 ; 0 ; 4). La droite D parallèle à la droite (AB) passant par le point C a pour représentation paramétrique : Coordonnées d'un vecteur directeur de la droite (AB), donc d'une droite parallèle à (AB) : xB-xA = -2 ; yB-yA = 3 ; zB-zA = 1 ou encore (-1 ; 1,5 ; 0,5). Représentation paramétrique de la droite D : x = -t+xC = -t-1. y =1,5t+yC =1,5t. z =0,5t+zC =0,5t +4 avec t réel. Réponse A. 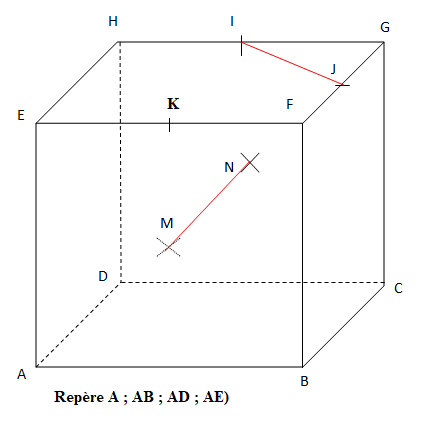Question 8. ABCDEFGH est un cube dont les faces ABCD et EFCH sont parallèles et de telle sorte que [AE] et[BF] soient deux arêtes avec E situé « au-dessus » de A. M est le centre de la face ABFE et N est le centre de la face BCGF. Les points I et J sont les milieux respectifs des arêtes [GH] et [FG]. Les droites (IJ) et (MN) sont : A. perpendiculaires. Faux. Deux droites du même plan sont perpendiculaires si elles se coupent à angle droit. B. orthogonales Faux. K étant le milieu de EF, les droites (IK) et (MN) sont parallèles. (IJ ) et ( IK) n'étant pas perpendiculaires, les droites (IJ) et (MN) ne sont pas orthogonales., C. sécantes, non perpendiculaires. Faux. D. parallèles. Faux. M(0,5 ; 0 ; 0,5 ) ; N ( 0,5 ; 1 ; 0,5) ; I (0,5 ; 1 ; 1) ; J(1 ; 0,5 ; 1). Coordonnées d'un vecteur directeur de (MN)  :(  0 ; 1 ; 0 ). Coordonnées d'un vecteur directeur de (IJ)  :(  0,5 ; -0,5 ; 0 ). ... .... Question 9. L’équation e2x−3ex−4 =0 admet dans l’ensemble des nombres réels : A. 0 solution B. 1 solution. Vrai. C. 2 solution D. plus de 2 solutions. On pose X = ex > 0. X2-3X-4=0 ; discriminant D = 9+4*4=25 = 52. Solution positive retenue : X = (3+5) / 2 =4 Question 10. Le plan est rapporté à un repère orthonormé. Soient f et g les fonctions définies sur [0 ; +∞[ respectivement par : f (x) = e−x cos(4x) et g(x) =0,5e−x . Les points communs aux deux courbes représentatives de ces deux fonctions ont pour abscisses : e−x cos(4x) =0,5e−x   ; cos(4x) =0,5 = cos(p/3) 4x =±p/3 +2kp avec k  appartenant à Z x =± p/12 +0,5kp. Question 11.  Un joueur lance une fois un dé cubique bien équilibré. Il gagne 10 € si le dé marque 1. Il gagne1 € si le démarque 2 ou 4. Il ne gagne rien dans les autres cas. Soit X la variable aléatoire égale au gain du joueur. La variance de X est ; 2; 12 ; 16 ; 17. Gain (€) 10 1 0 Probabilité 1 /6 2 /6 3 /6 écart à la moyenne +8 -1 -2 Moyenne : (10 +2) / 6 =2. Variance : ( 82+(-1)2 *2+ (-2)2x3) / 6=78 /6 =13. . Question 12. Suite télescopique Soit n un entier naturel non nul. La limite de l’expression suivante lorsque n tend vers +∞est : 0 ; ln(2) ; +oo vrai ; -ln(2). 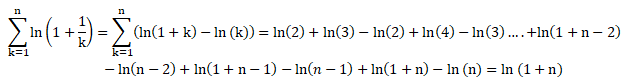Question 13. Suite doublement télescopique Soit n un entier naturel supérieur ou égal à 2. La limite de l’expression suivante lorsque n tend vers +oo est : 0 ; ln(2) ; +oo ; -ln(2) vrai. 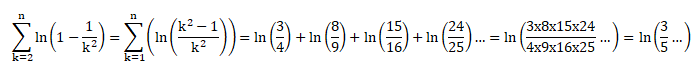Question 14. On jette deux dés cubiques non pipés, l’un bleu et l’autre rouge. Les faces de chacun des dés sont numérotées de 1 à 6. On note a le nombre de la face apparente du dé bleu et b celui du dé rouge. Soil E l’équation du second degré dans l’ensemble des nombres réels : x2−2ax +b2= 0. Identifier la ou les affirmation(s) vraie(s) parmi les suivantes : A. La probabilité que E ait une racine double est 1/6. Vrai. B. La probabilité que E n’ait aucune racine réelle est égale à la probabilité que E ait deux racines réelles distinctes. Vrai. Si a > b , il y a 2 racines réelles ( 15 cas posibles sur 36). Si a < b , il n'y a pas de racines réelles ( 15 cas posibles sur 36). C. Si E a deux racines réelles distinctes, la probabilité que l’une soit égale à 1 est 1 /3. Faux. 5 cas possibles sur 36. D. La probabilité que E ait une racine double paire est 1 / 36. Faux ( 3 / 36 = 1 / 12).  a et b sont des entiers compris entre 1 et 6, bornes comprises. x2−2ax +b2= 0 ; discriminant D = 4a2-4b2 =4(a2-b2). Si a = b, il existe une racine double x = a. Soit 1,1 ; 2, 2 ; 3,3 ; 4, 4 ; 5, 5 ; 6,6 sur 36 cas possibles. Si a > b, il existe deux racines réelles. x=(2a ± 2(a2-b2)½) / 2 =a ±(a2-b2)½. a 1 2 3 4 5 6 b 1 1 1 2 1 3 1 4 1 5 1 6 1 2 1 2 2 2 3 2 4 2 5 2 6 2 3 1 3 2 3 3 3 4 3 5 3 6 3 4 1 4 2 4 3 4 4 4 5 4 6 4 5 1 5 2 5 3 5 4 5 5 5 6 5 6 1 6 2 6 3 6 4 6 5 6 6 6 Question 15. Une usine fabrique des vis de 2 cm de mesure de longueur. On note X la variable aléatoire ayant pour valeurs les mesures de longueurs des vis possibles exprimée en cm, la probabilité pi qu’une vis soit de longueur xi . xi 1,8 1,9 2 2,1 2,2 pi 1/12 1/6 0,5 1/6 1/12 A. Si nous prélevons au hasard et avec remise 6 vis, la probabilité d’avoir au moins une vis de mesure de longueur 1,8 cm est (1/12)6. Faux. X suit la loi binomiale. "au moins une vis" signifie 1, ou 2, ou 3, ou 4, ou 5, ou 6 vis.de longueur 1,8 cm. Probabilité d’avoir au moins une vis de mesure de longueur 1,8 cm : 1-P(X=0) = 1-(60)(1/12)0 x(11/12)6 =1-(11/12)6 =(126-116) /126 = B. Si nous prélevons au hasard et avec remise 6 vis, la probabilité d’avoir exactement deux vis de mesure de longueur 1,8 cm est 6x114 / 126. Faux. P(X=2) = (6 2) (1/12)2 (1-1/12)4=6 x5 /2 (1/12)2 (1-1/12)4=15x(1/12)2 (11/12)4=15x114 / 126. C. Si nous prélevons au hasard et avec remise 6 vis, la probabilité d’avoir au moins une vis de mesure de longueur supérieure ou égale à 1,9 cm est 1−(11/12)6. Faux. " avoir au moins une vis de mesure de longueur supérieure ou égale à 1,9 cm" signifie vis de longueur 1,9 cm ou 2 cm ou 2,1 cm ou 2,2 cm. 1-P(X=1)=1- (6 1) (1/6)1 (1-1/6)5=1-6 /6 x(5 / 6)5 =1-(5 / 6)5. D. Si l’on prélève au hasard une vis, la probabilité qu’elle soit au moins de 2 cm est 3 /4. Vrai. "au moins de 2 cm" signifie 2 cm ou 2,1 cm ou 2,2 cm. 0,5 +1/6 +1 /12 = (6 +2+1) / 12 =9 /12 =3 /4.

menu