Mathématiques,
technicien supérieur de l'aviation 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Partie 1.
On considère la fonction f définie sur l’intervalle [−2 ; 2] par :
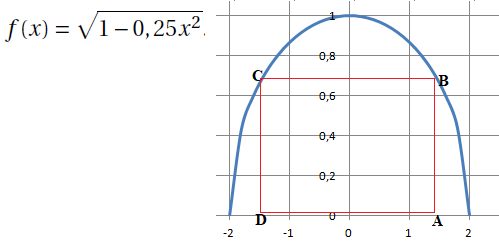
et Cf sa courbe représentative dans un repère orthonormé.
Question 1.
Un calcul de f (−x) donne
A. f (−x) = f (x) : la fonction f est impaire. Faux, la fonction est paire.
B. f (−x) = −f (x) : la fonction f est paire. Faux.
C. Le point O(0; 0) est centre de symétrie de Cf .
D. La droite d’équation x = 0 est axe de symétrie de Cf . Vrai.
Question 2.
Le calcul de la dérivée f ′ de la fonction f donne :
On pose u =1- 0,25 x2 ; u' = -0,5 x.
f(u) = u½ : f '(u) = ½u' u-½ ; f '(x) = -0,25 x(1-0,25x2)-½.
Question 3.
Ainsi, on en déduit :
A. La fonction f est croissante sur ]−2 ; 0[ et décroissante sur ]0; 2[. Vrai.
B. La fonction f est décroissante sur ]−2 ; 0[ et croissante sur ]0; 2[. Faux.
C. La fonction f est croissante sur ]−2 ; 2[. Faux.
D. La fonction f est décroissante sur ]−2 ; 2[. Faux.
Pour tout réel x de l’intervalle ]0; 2[, on note :
A le point de coordonnées (x ; 0),
D le point de coordonnées (−x ; 0),
B le point de coordonnées (x ; f (x)),
et C le point de coordonnées (−x ; f (−x)).
Question 4.
Soit g la fonction qui à tout réel x de l’intervalle ]0; 2[ associe l’aire du rectangle ABCD.
On a : g(x) = 2x f(x) = 2x(1-0,25x2)½= (4x2-x4)½. Réponse C.
Question 5.
Ainsi, la dérivée g′ de la fonction g sur ]0; 2[ peut s’écrire :
On pose u =4x2-x4 ; u' = 8 x-4x3.
g(u) = u½ : g '(u) = ½u' u-½ ; g '(x) = (4 x-2x3)(4x2-x4)-½ =(4 x-2x3) / (2x) (1-0,25x2)-½=(2-x2) (1-0,25x2)-½. Réponse D.
Question 6.
L’aire du rectangle ABCD est alors maximale pour :
g'(x) = 0 ; 2-x2 = 0 ; x = 2½.
Réponse B.
.
Question 7.
La valeur maximale S de cette aire est ainsi :
S =g(2½)=(4*2-4)½=2.
. Réponse A.
Partie II.
Un joueur débute un jeu vidéo et effectue plusieurs parties successives. On admet que :
• la probabilité qu’il gagne la première partie est 0,1 ;
• s’il gagne une partie, la probabilité de gagner la suivante est égale à 0,8 ;
• s’il perd une partie, la probabilité de gagner la suivante est égale à 0,6.
On note, pour tout entier n non nul :
Gn l’évènement « le joueur gagne la n-ième partie » ;
pn la probabilité de l’évènement Gn.
On a donc p1 = 0,1.
Question 8.
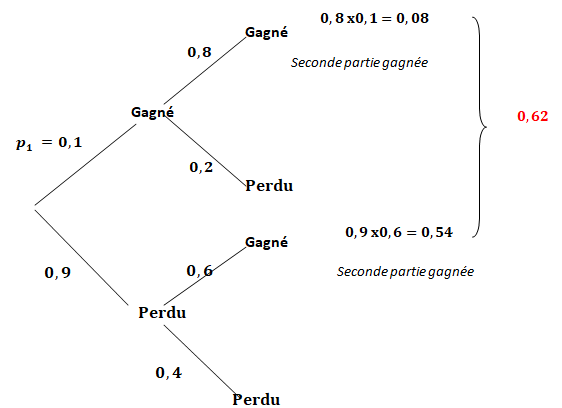
On montre que p2 =0,6 ; 0,78 ; 0,62 vrai ; 0,8.
Question 9.
Le joueur a gagné la deuxième partie. La probabilité p qu’il ait perdu la première est :
1 /19 : 18 /31 ; 4 / 19 ; 27 / 31.Vrai.
0,54 / 0,62 = 54 / 62 = 27 / 31.
Question 10.
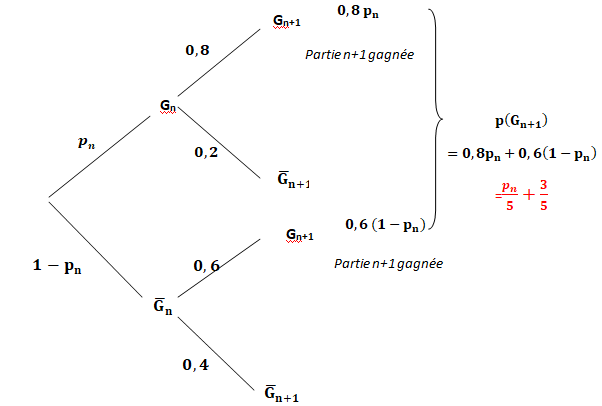
On montre, que pour tout entier naturel n non nul :
A. pn+1 =pn / 5 +3 /5. Vrai.
Dans ce cas p2 =0,1 / 5 +3 / 5 =3,1 / 5=0,62.
B. pn+1 = 2 /5 -pn /5.
Dans ce cas p2 =2 / 5 -0,1 / 5 =1,9 / 5=0,38 différent de 0,62.
C. pn+1 =4pn / 5 +0,1.
Dans ce cas p2 =0,4 / 5 -0,1 =1,9 / 5=0,18 différent de 0,62.
D. pn+1 =0,9 -4pn /5.
Dans ce cas p2 =0,9 -0,4 / 5 =1,9 / 5=0,82 différent de 0,62.
Question 11.
Ainsi, pour tout entier naturel n non nul :
A. pn =1 /3 -7 /6(-1/5)n.
Dans ce cas p2 =1 / 3 -7 / (6x25) =1,9 / 5~0,28 différent de 0,62.
B. pn =3 /4 -13 /4(1/5)n. Vrai.
Dans ce cas p2 =0,75 -13 /100 =0,62.
C. pn =1 /2 -1 /2(4/5)n.
Dans ce cas p2 =0,5 -0,5x16 / 25 =0,18 différent de 0,62.
D. pn =1 /2 +1 /2(-4/5)n.
Dans ce cas p2 =0,5 +0,5x16 / 25 =0,82 différent de 0,62.
Toutes les propositions sont fausses.
Question 12.
Quand n tend vers plus l'infini, pn tend vers : 0,5 ; 0,75 vrai ; 1 /3 ; +oo.
-1 < 1 /5 < 1, donc (1 /5)n tend vers zéro si n tend vers plus l'infini ;
par produit et addition pn tend vers 0,75.
|
...
|
....
|
Partie III.
Les questions de cette partie sont indépendantes
Question 13.
On considère, dans le plan complexe muni d’un repère orthonormal direct les points A, B et C d’affixes respectives :
a = 1+i, b = 3i, c =(3½+0,5)+ i(0,5 x3½ +2)
A. Le triangle ABC est un triangle rectangle.
B. Le triangle ABC est un triangle isocèle. Vrai.
C. Le triangle ABC est un triangle équilatéral. Vrai.
D. Le triangle ABC est un triangle ni rectangle, ni isocèle, ni équilatéral.
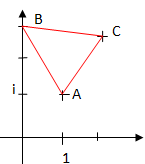
AB = |zB-zA|=(12+22)½ =5½.
AC = |zC-zA|=((3½-0,5)2+(0,5 x3½ +1)2)½ =(3,25 -3½+1,75+3½)½ =5½.
BC = |zC-zB|=((3½+0,5)2+(0,5 x3½ -1)2)½ =(3,25 +3½+1,75-3½)½ =5½.
Question 14.
Soit le nombre complexe z =(3½+i)1515.
A. Le nombre complexe z est un réel.
B. Le nombre complexe z est un imaginaire pur. Vrai.
C. arg(z) = 1515 p /3 +2k p, k ∈ Z.
D. |z| =(2½)1515.
z1 = 3½+i ; |z1 | =(3 +1)½ = 2.
z1 / |z1 | =3½ / 2 +0,5 i =cos (p/6) + i sin(p/6) = exp(p/6).
|z| = 21515.
arg (z )= 1515 xp / 6 =505 p /2 =(126 x 2 +0,5)p= 0,5 p +2kp avec k = 126
.
Question 15.
Dans le plan muni d’un repère orthonormé, on note S l’ensemble des points M dont l’affixe z vérifie les conditions :
|z −1| = |z −i| et |z −1−2i| < 3.
On désigne par C le cercle de centre le point de coordonnées (1 ; 2) et de rayon 3, et par D la droite d’équation y = x.
A. L’ensemble S est la réunion des ensembles C et D.
B. L’ensemble S est l’intersection des ensembles C et D.
C. Soient A et B les points d’intersection de C et D. L’ensemble S est le segment [AB]. Vrai.
D. L’ensemble S est réduit au point I(0,5 ; 0,5).
Equation du cercle : (x-1)2 +(y-2)2 = 9.
z = x+iy ; |z-1| =((x-1)2 +y2)½.
|z-i| =((y-1)2 +x2)½.
|z −1| = |z −i| donne : (x-1)2 +y2=(y-1)2 +x2 ; x2-2x+1+y2 =y2-2y+1+x2 ; y = x.
Les points M appartienent à la droite D.
|z −1−2i| =( (x-1)2 +(y-2)2)½ = 3.
Les points M appartienent disque de centre (1 ; 2).
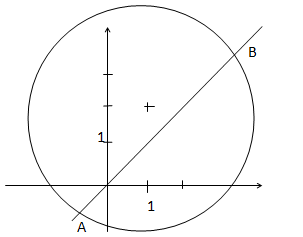
L'ensemble S est l'ensemble des points de la droite D situés à l'intérieur du disque.
|
|