Mathématiques,
 concours TSEEAC technicien supérieur de l'aviation civile 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.
.. ..
......


...
Partie I.
Max doit se rendre en voiture dans une ville voisine pour un rendez-vous à 15 h 15. Il quitte son domicile entre 13 h et 14 h à un instant 13 +t ou t est compris entre [0 ; 1]. La durée du trajet est estimée à t+0,5.
Question 1.
La probabilité p1 que Max ne soit pas en retard à son rendez-vous est :
A. 0,125 ; B. 0,25 ; C. 0,75 ; D. 0,875. Vrai.
Origine des dates : 13 h. ( 15 h15 correspond à 2,25)
t+t+0,5 < 2,25.
2t < 1,75 ; t < 0,875.
P(t < 0,875) = 0,875 /1=0,875.

Question 2.
La probabilité p2 que Max arrive avec exactement un quart d'heure d'avance est ;
A.  0,125 ; B.  0,25. C.  0,75. D.  0,875.
Origine des dates : 13 h. ( 15 h correspond à 2)
t+t+0,5 =2.
2t = 1,5 ; t = 0,75.
P(t = 0,75) =0,01 ( une seule valeur sur 100 possibles).
E : aucune des réponses proposées.

 Question 3.
 La probabilité p3 que Max soit en retard de plus de 9 minutes est ;
A. 0,05. Vrai. B. 0,13. C. 0,87. D. 0,95.
Origine des dates : 13 h. ( 15 h 24 correspond à 2,4)
t+t+0,5 > 2,4.
2t > 1,9 ; t > 0,95.
P(t > 0,95) = 0,05 /1=0,05.

 Question 4.
 La probabilité p4 que Max arrive entre 14h54 et 15h06 est ;
A. 0,1. Vrai.  B. 0,26. C. 0,52. D. 0,78.
Origine des dates : 13 h. ( 14 h 54 correspond à 1,9 ; 15 h 06 correspond à 2,1 )
1,9 < t+t+0,5 < 2,1.
0,7 < t < 0,8.
p3 = (0,8-0,7) /1=0,1.

 Question 5.
Pour arriver entre  entre 14h54 et 15h15 Max doit partir :
A. entre 13h32 et 13h48.  B. entre 13h42 et 13h52. Vrai. C.entre 13h53 et 14h21. D. entre 14h02 et 14h18.
15 h 15 correspond à 2,25.
1,9 < t+t+0,5 < 2,25.
  0,7 < t < 0,875.
Soit entre 13h42 et 13h525.

 Partie 2.
On administre à un patient un médicament par injection intraveineuse. La quantité de médicament diminue en fonction du temps. On étudie l'évolution de cette quantité minute par minute.
Question 6.
A t=0, on effectue une injection de 10 mL. 20 % de ce médicament est éliminé par minute. On note un la quantité de médicament restant dans le sang au bout de n minutes. La suite (un) est :
A. arithmétique  u0 = 10, raison r = 2.
B. arithmétique  u0 = 10, raison r = -2.
C. géométique  u0 = 10, raison q = 0,2.
D. géométique  u0 = 10, raison q = 0,8.Vrai.
u1 = 0,8 u0 ; u2 = 0,8 u1.

Question 7.
On en déduit que :
A un =10 -2n ; B. un = 10 +2n ; C. un = 8 (0,8)n-1 vrai ; D. un = 10 (0,2)n .
un = u0 qn =10 x 0,8n =10 x0,8 x0,8 n-1.

 Question 8.
On donne 1,2520 ~86,74. La quantité de médicament restant dans le sang devient inférieure à 1 % de la quantité initiale au bout de :
A. 5 minutes ; B. 19 minutes ; C. 20 minutes ; D. 21 minutes vrai.
10 x0,01 = 0,1.
10 x 0,8n < 0,1 ; 0,8n < 0,01 ; 1/1,25n < 0,01 ; 1/ 86,74 > 0,01 ; 1,2521 ~86,74 x1,25 ~108 ; 1/108 <0,01.

Question 9.
On injecte à t = 0, 10 mL de médicament. Toutes les minutes on injecte 1 mL de médicament. On note wn la quantité de médicament en mL présente dans le sang au bout de n minutes. La suite (wn) vérifie :
A. Wn+1 =0,2 wn +1 ; B. Wn+1 =0,2( wn +1) ; C. Wn+1 =0,8 wn +1 vrai ; D. Wn+1 =0,8 (wn +1).
w0 = 10 ; w1 = 0,8 w0 +1 ; w2 = 0,8 w1 +1.

Question 10.
On pose zn = wn-5. La suite (zn) vérifie :
A. géométrique : z0 = 5 ; raison q = 0,8 vrai ; B. géométrique : z0 = 5 ; raison q = 0,2 ;
C. arithmétique : z0 = 5 ; raison r = 2 ; D. arithmétique : z0 = 5 ; raison r = -2.
zn+1 = wn+1-5 =0,8 wn +1-5 =0,8 wn -4 =0,8(wn-5) =0,8 zn.

Question 11.
On en déduit l'expression de wn en fonction de n :
A. wn = 5(1-0,8)n+5 ; B. wn = 5(1-0,2)n+5 ; C. wn =2(5+n) ; D. wn =2(5-n).
zn = =5*0,8n ; wn  =zn+5=5*0,8n +5= 5(0,8n +1).
E : aucune des réponses proposées.

Question 12.
Par passage à la limite on obtient :
A. en plus l'infini, la limite de wn vaut -oo ; B. en plus l'infini, la limite de wn vaut 0 ;
 C. en plus l'infini, la limite de wn vaut 5 vrai ; D. en plus l'infini, la limite de wn vaut +oo.
-1 < 0,8 <1, 0,8n tend vers zéro si n tend vers plus l'infini.
 5(0,8n +1) tend vers 5.

 Partie III.
Soit f(x) =(2+cos x) e1-x définie sur R.

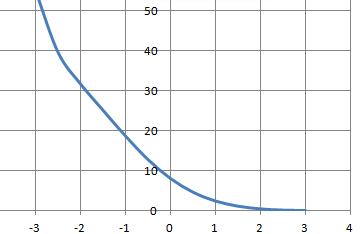Question 13.
f(x) vérifie :
A. il existe un réel a tel que f(x) < 0 si x < a et f(x) > 0 si x > a.
 B. il existe un réel a tel que f(x) > 0 si x < a et f(x) < 0 si x > a.
 C. Pour tout réel x, f(x) < 0.
 D. Pour tout réel x, f(x) > 0. Vrai.
-1 < cos x <+1 ; 2+cos x >0 ; e1-x > 0.

Question 14.
La fonction f ' est :
On pose u =2+cos x ; v = e1-x  ; u' = -sin x ; v' = -e1-x  ;
f '(x) = u'v+v'u = -sin x e1-x -(2+cos x) e1-x  = -(2+cos x+ sin x) e1-x . Réponse C.

 Question 15.
On montre que pour tout x :.
A. 2½ cos (x-p/4) = cos x -sin x.
 B. 2½ cos(x-p/4) = cos x +sin x.
 C. 2½ cos (x+p/4) = cos x +sin x.
 D. 2½ cos (x+p/4) = cos x -sin x.
sin a cos b = 0,5(sin (a+b) +sin (a-b).
2 x 2½ /2 cos (x+p/4)=2 sin (p/4) cos (x+p/4) =sin (x+p/4+p/4) +sin (-x) = -cos x + sin (-x).
E : aucune des réponses proposées.
 
Question 16.
La fonction f ' vérifie :
A. Pour tout x réel, f '(x) < 0.
B. Pour tout x réel, f '(x) > 0.
C. il existe un réel ß tel que f '(x) < 0 si x < ß et f '(x) > 0 si x > ß.
D.  il existe un réel ß tel que f '(x) > 0 si x < ß et f '(x) < 0 si x > ß.
f '(x) =-(2+cos x+ sin x) e1-x .
e1-x >0 ; (2+cos x+ sin x) > 0 ; -(2+cos x+ sin x) < 0. f '(x)  < 0.
E : aucune des réponses proposées.

Question 17.
On montre :
A. limite en plus l'infini de f(x) =+oo et limite en moins l'infini de f(x) =-oo
B.  limite en plus l'infini de f(x) =+oo et limite en moins l'infini de f(x) =0
C. limite en plus l'infini de f(x) =0 et limite en moins l'infini de f(x) =-oo
D.   limite en plus l'infini de f(x) =-oo et limite en moins l'infini de f(x) =+oo.
E : aucune des réponses proposées.
1 <(2+cos x) < 3
e1-x tend vers +oo si x tend vers -oo ;
e1-x tend vers 0 si x tend vers +oo.

Question 18.
Soit A l'aire de la partie du plan délimitée par la courbe C représentant f, l'axe des abscisses et les droites d'équations x=0 et x = 1. On a en unité d'aire :

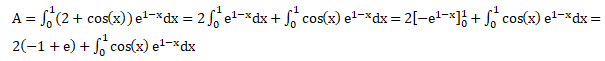
Réponse B.

Question 19.
Soit f1(t) = cos (t) e1-t et f2(t) = sin (t) e1-t pour tout réel t. On peut montrer que :
A. f1(t) = 0,5[f '2(t) -f '1(t)]. Vrai.
B. f1(t) = 0,5[f '1(t) -f '2(t)].
C. f2(t) = 0,5[f '2(t) +f '1(t)].
D. f2(t) = -0,5[f '2(t) +f '1(t)]. Vrai.
f '1(t) : on pose u =cos t ; v = e1-t  ; u' = -sin t ; v' = -e1-t  ;
f '1(t) = u'v+v'u = -sin t e1-t -cos t  e1-x  = -(cos t+ sin t) e1-t .
f '2(t) : on pose u =sin t ; v = e1-t  ; u' = cos t ; v' = -e1-t  ;
f '2(t) = u'v+v'u = cos t e1-t -sin t  e1-x  = (cos t- sin t) e1-t .
f '2(t) -f '1(t)=2 cos t e1-t .
f '2(t) +f '1(t)= -2 sin t e1-t .

Question 20.
On en déduit que A = :

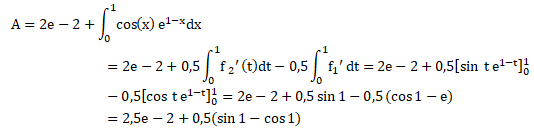
Réponse B.

...
....

 Partie IV.
Soit les nombres complexes z1 =1-i et z2 = (6½-i 2½) / 2.
Question 21.
Les formes exponentielles de ces nombres s'écrivent :
|z1| = (12+(-1)2)½ = 2½.
z1 / |z1| =1 / 2½ -i / 2½ =cos (-p /4) + i sin (-p /4).
z1 =2½ exp(-ip/4).
|z2| = (6+2)½ / 2= 2½.
z2 / |z2| = (3½-i ) / 2=cos (-p /6) + i sin (-p /6).
z2 =2½ exp(-ip/6). Réponse C.

Question 22.
Le nombre complexe z1 / z2 s'écrit sous forme exponentielle :
exp(-ip/4) / exp(-ip/6)= exp ( i(-p/4 +p/6) = exp( i(-p/12). Réponse D.

 Question 23.
Le nombre complexe z1 / z2 s'écrit sous forme algébrique :
2(1-i) / (6½-i 2½) =2(1-i) (6½+i 2½) / [(6½-i 2½)(6½+i 2½)]
=2 (1-i) (6½+i 2½) / 8 =[(6½+ 2½)+ i(2½-6½)] / 4. Réponse C.

Question 24.
On en déduit que :
[(6½+ 2½)+ i(2½-6½)] / 4 = cos (-p /12) + i sin (-p /12).
cos (-p /12) =(6½+ 2½) / 4 et sin (-p /12) =(2½-6½) / 4. Réponse A.

Question 25.
On en déduit que :
[(6½+ 2½)+ i(2½-6½)] / 4 = cos (-p /12) + i sin (-p /12).
cos (-p /12) = cos(p /12) = (6½+ 2½) / 4 et sin (-p /12) = -sin (p /12) = (2½-6½) / 4.
sin (p /12) =- (2½-6½) / 4 = (6½-2½) / 4 . Réponses B et C.



  
menu