Etude d'un gymnase, acoustique, transferts thermiques, corrosion, BTS EEC 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Les gymnases sont des salles polyvalentes aux usages multiples : sports et événements réguliers. Les gymnases sont utilisés par des établissements scolaires, des clubs sportifs et des mairies. Différents aspects, comme l'acoustique du gymnase et son confort thermique, contribuent à inciter à la pratique du sport et à l'utilisation de la structure. L’objectif du sujet est d’étudier l’acoustique, les transferts thermiques et le chauffage de l’eau des sanitaires d’un gymnase. Le gymnase étudié sera modélisé par un parallélépipède rectangle de longueur L = 44,0 m, de largeur l = 24,0 m et de hauteur H = 10,0 m. Dans une salle de sport, on recommande une durée de réverbération comprise entre 0,8 s et 1,6 s. A.1.Citer deux problèmes acoustiques présents dans un gymnase. Il faut contrôler le niveau sonore élevé causé par les utilisateurs du gymnase et par la réverbération. Les matériaux absorbants le son qui seront installés ne constituerons pas une gêne. A.2. Expliquer en quoi consiste le phénomène de réverbération et en quoi ce phénomène peut être gênant dans un gymnase. La réverbération est la persistance du son dans un lieu clos après interruption de la source.sonore. A.3. On admet que le temps de réverbération TR dans un local est donné par la loi de Sabine, avec A l’aire d'absorption équivalente et V le volume du local étudié. TR = k ·V / A avec k = 0,16 (SI) , TR(s), V (m3) et A (m2) On donne l’expression de l’aire d’absorption équivalente (qui est égale à la somme des aires équivalentes des surfaces) : 𝐴= a1·S1+ a2·S2+⋯ avec ai· les coefficients d’absorption des surfaces et Si les surfaces correspondantes. A.3.1. Donner, en la justifiant, l'unité de k dans le système international. k = TR A / V soit s m2 m-3 soit s m-1. A.3.2. Compléter le tableau  pour calculer l'aire d'absorption équivalente totale A de la salle de sport du gymnase. paroi étudiée matériau ai Si m2 Ai m2 Parois verticale intérieures non vitrées bois 0,175 1260 1260 x0,175=220,5 Parois vitrées et portes Plexiglas et bois 0,120 100 0,12 x100 = 120 sol PVC 0,0500 44 x24=1056 1056x0,05=52,8 plafond bois et métal 0,0800 1056 1056x0,08=84,8 mobilier bois et PVC 5,00 A= 482,8 A.3.3. Calculer le temps de réverbération TR correspondant. Commenter la valeur obtenue. Volume : 44 x24 x10 =10560 m3. TR = k ·V / A=0,16 x 10560 /482,8=3,5 s. Cette valeur est trop élevée. A.4. Après un mois d'utilisation, la réverbération a été jugée trop importante. La solution acoustique choisie est de suspendre des plaques revêtues de matériau absorbant. A.4.1. Les temps de réverbération ont été mesurés avant et après le traitement acoustique comme le montre les courbes ci-dessous. Déterminer la valeur TR’ du temps de réverbération mesuré avec les dalles acoustiques, à 1000 Hz à l’aide du document ci-dessous. 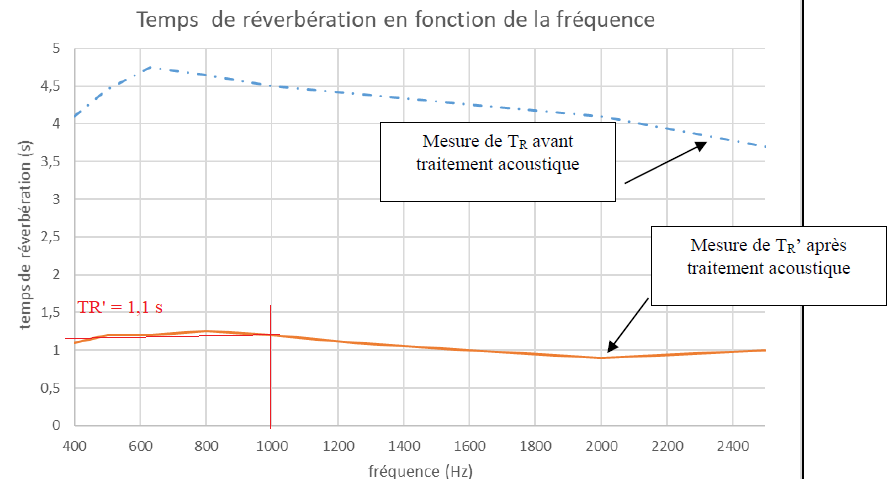Source: http://www.acusticaintegral.fr/200003995/ilots-acoustiques-dans-un-gymnase-scolaire/ A.4.2. Calculer alors la nouvelle aire d'absorption équivalente A’ correspondante de la salle du gymnase après traitement acoustique. TR' = k ·V / A' ; A' = kV / TR' = 0,16 x 10560 /1,1 ~1500 m2. A.4.3. Sachant que chaque dalle a une aire d'absorption équivalente de 24,0 m2, qu'elles ne sont pas collées au plafond mais suspendues, leur absorption se rajoute à celle du plafond existant. Calculer le nombre de dalles à installer au plafond. Commenter la valeur obtenue. (1500-482,8) / 24 ~44 dalles. Cette valeur n'étant pas très élevée, cela est réalisable. ... .... B. Échanges thermiques au niveau du plancher chauffant (7 points) Certains gymnases sont chauffés grâce à un plancher chauffant basse température. B.1.  Citer deux avantages d'un plancher chauffant. Posé de façon invisible, il ne peut pas être endommagé ;  pas d'éléments de chauffage gènant, pas de réduction de la surface utile. Le coût d'installation n'est pas très élévé; elle ne nécessite que peu d'entretien. B.2. La figure ci-dessous représente la coupe verticale d'un sol sportif dans lequel on a incorporé ce système de chauffage. Celui-ci est constitué d'un tube dans lequel circule de l'eau à température moyenne supposée constante qe = 40 °C. La température intérieure à maintenir dans le gymnase est de qi = 18 °C. On assimilera le système de chauffage à un plan horizontal de 1 056 m2 de surface. On note qF = 2 °C la température du sol de fondation. 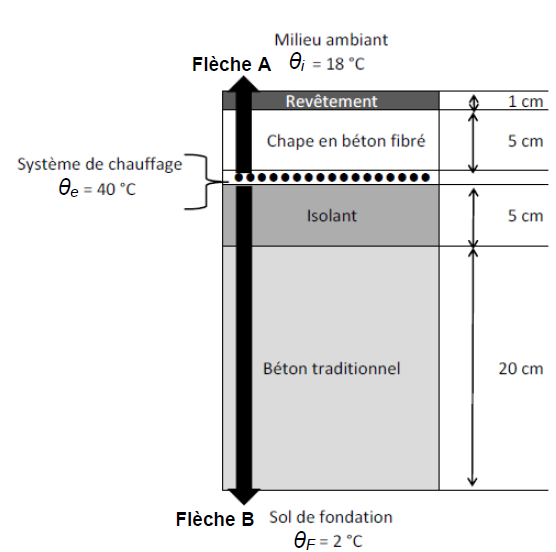La résistance thermique d'échange superficiel au niveau du revêtement sportif est rs = 0,10 m2·K·W-1. B.2.1. Exprimer et calculer rSUP la résistance thermique surfacique comprise entre le système de chauffage et l'intérieur de la pièce à chauffer. l béton fibré =1,8 W m-1 K-1 ; S = 1056 m2 ;   résistance thermique du béton fibré : e / (l béton fibré) =0,05 /1,8 =0,028 K m2·W-1. rSUP = 0,028 +0,10 = 0,128 K m2·W-1. B.2.2. Vérifier que le flux thermique correspondant a pour valeur FSUP = 176 kW. S(qe-qi) / rSUP = 1056 x(40-18) / 0,128 ~180 kW. B.2.3. Montrer que le flux thermique FINF transmis du système de chauffage au sol de fondation est proche de 15 kW. résistance thermique : r = eisolant / lisolant +  ebéton / lbéton =0,05 / 0,02+0,20/1,4 =2,64 m2·K·W-1. S(qi-qF) / r = 1056 x(40-2) / 2,64 ~15 200 W~15 kW. B.2.4. Indiquer quelle flèche noire A ou B correspond aux pertes thermiques et quelle flèche noire correspond au flux thermique utile. A : flux thermique utile ; B : pertes thermiques. B.2.5. On désire limiter les pertes vers le sol de fondation à 5 % de la puissance totale fournie par le système de chauffage. Indiquer si c’est le cas pour le système étudié. Sinon, proposer une solution technique. Ptotale = 176+15=191 kW. 15 /191~ 0,079 (7,9 %) Il faut augmenter l'épaisseur d'isolant. C. Protection contre la corrosion de la cuve du chauffe-eau des sanitaires (6 points) Dans les sanitaires de ce gymnase se trouve un chauffe-eau électrique constitué d'une cuve en acier. On supposera que l'acier se comporte comme son principal constituant : le fer. Afin de prolonger la durée de vie de la cuve et donc du chauffe-eau, une anode métallique est placée à proximité de la résistance électrique. C.1. Étude de la corrosion sans anode métallique. L'acier, principalement constitué de fer, est un matériau qui s'oxyde en ions Fe2+ au contact du dioxygène dissout dans l'eau. C.1.1. Écrire la demi-équation électronique qui modélise l'oxydation du fer. Fe (s)--> Fe2+ + 2e-. C.1.2. Compléter la demi-équation électronique du couple redox O2 / HO- : O2 + ..2. H2O + .4. e- = 4 HO- C.1.3. À l'aide des 2 demi-équations électroniques précédentes, écrire l'équation de la réaction de corrosion du fer. 2 fois {Fe (s)--> Fe2+ + 2e- } O2 + ..2. H2O + .4. e- = 4 HO- Ajouter : 2Fe (s) + O2 + ..2. H2O + .4. e- --> 2Fe2++ 4e- + 4 HO-. Simplifier : 2Fe (s) + O2 + ..2. H2O  --> 2Fe2+ + 4 HO-. C.1.4. Indiquer les risques pour la cuve du chauffe-eau si celle-ci n'est pas protégée contre la corrosion. La cuve finira par se percer. C.2.1. À partir des valeurs de potentiels standard, expliquer pourquoi une anode en magnésium empêche l'oxydation de la cuve en acier et pourquoi elle est dite « sacrificielle ». Le magnésium est plus réducteur que le fer ; le magnésium s'oxyde à la place du fer et protège ce dernier contre la corrosion. C.2.2. Écrire la demi-équation électronique qui a lieu au niveau de l’anode en magnésium. Mg(s) --> Mg2+ + 2e-. C.2.3. Compléter le schéma en indiquant le sens de circulation des électrons entre l’anode et la cuve. 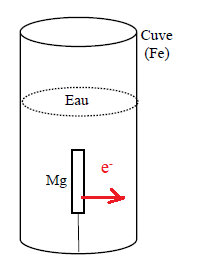Les électrons se dirigent du magnésium vers le fer de la cuve. C.3. Initialement, l'anode de magnésium est un cylindre de masse m = 830 g. En moyenne, la vitesse de corrosion du magnésium est de v = 3,86 × 103 C par jour. Déterminer le temps au bout duquel il faudra remplacer cette pièce en respectant le taux d'usure. Exprimer le résultat en années. M(Mg) =24,3 g / mol. Quantité de matière de magnésium n = m / M = 830 / 24,3 ~34,16 mol. Quantité de matière d'électrons : 2 n= 68,31 mol. Quantité d'électricité correspondante : 2 n F = 68,31 x 96500 =6,59 106 C. Durée : 6,59 106 / (3,86 103) ~1,71 103 jours ou environ 4,7 ans.

menu