Mathématiques, brevet DNB, Amérique du Nord 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. 22 points. 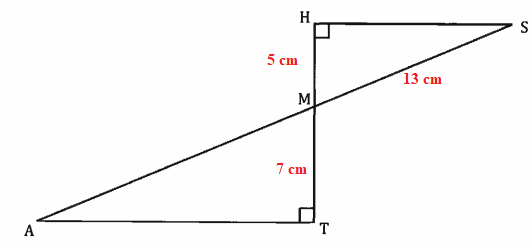 1. Démontrer que HS = 12 cm.. Relation de Pythagore dans le triangle rectangle MHS : HS2 = MS2 -MH2 =132-52=144 ; HS = 12 cm.  2. Calculer AT. Les deux triangles MHS et MTA sont semblables : MT / MH = AT / HS ; AT = MT x HS / MH = 7 x 12 / 5 = 16,8 cm. 3. Calculer la mesure de l'angle HMS. tan (MAT) = MT / AT = 7 / 16,8 =0,417 ; L'angle mesure environ 23°. 4. Quelle transformation permet d'obtenir le triangle MAT à partir du triangle MHS ? Une homothétie de centre M et de rapport 7 /5 = 1,4..   5. Sachant que MT = 1,4 MH, un élève affirme : "l'aire du triangle MAT est 1,4 fois plus grande que celle su triangle MHS. " Cette affirmation est-elle vraie ? Justifier. Aire du triangle MAT : MT x AT / 2 . Aire du triangle MHS : MH x HS / 2 . MT = 1,4 MH et AT = 1,4 xHS. Aire du triangle MAT = 1,4 2 x aire du triangle MHS. L'affirmation est fausse.   Exercice 2 QCM( 15 points) On lance un dé équilibré à 20 faces numérotées de 1 à 20. La probabilité pour que le numéro tiré soit inférieur ou égal à 5 est 5 cas favorables (1, 2,3, 4,5) sur 20 possibilités, donc la probabilité est 5 /20 = 1 /4 ( réponse B). Une boisson est composée de sirop et d'eau dans la proportion d'un volume de sirop pour 7 volumes d'eau. La quantité d'eau nécessaire pour préparer 560 mL de cette boisson est : Un volume correspond à : 560 /8 = 70 mL de sirop et 70 x7 = 490 mL d'eau. ( réponse D).   4. La décomposition en produit de facteurs premiers de 195 est : 195 = 3 x 5 x 13 (Réponse B). 5. 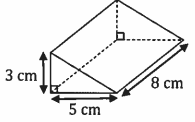Le volume de ce prisme droit est : Aire de base = 5 x3 /2  =7,5 cm2. Hauteur = 8 cm. Volume = 7,5 x8 =60 cm3. Réponse B. Exercice 3. 20 points. Sur 1,6 millions d'adolescents  interrogés, 81 % ne pratiquent pas d'activité physique régulière. 1. Combien ne respectent pas cette recommandation ? 1,6 x 0,81 =1,296 millions. Un adolescent décide de  faire au moins une heure de pratique physique par jour. Il note la durée quotidienne de cette pratique pendant 14 jours. jour 1 jour 2 jour 3 jour 4 jour 5 jour 6 jour 7 50 min 15 min 1 h 1 h 40 min 30 min 1 h 30 min 40 min jour 8 jour 9 jour 10 jour 11 jour 12 jour 16 jour 14 15 min 1 h 1 h 30min 30 min 1 h 1 h 0 min   a. Quelle est l'étendue de cette série ? 0 à 1 h 40 min soit de 0 à100 min. b. Donner la médiane. 0 ; 15 ; 15 ;  30 ; 30 ; 40 ; 50 ; 60 ; 60 ; 60 ; 60 ; 90 ; 90 ; 100 minutes. La médiane est comprise entre 50 et 60 min, par exemple (50 +60) / 2 = 55 min. 3.a. Montrer que l'objectif n'est pas atteint. Calcul de la moyenne : (0 +15 + 15 +  30 + 30 + 40 +50 + 60 + 60 + 60 + 60 + 90 + 90 + 100) / 14 =50 min, valeur inférieure à 1 h. b. Durant les 7 jours suivants, il consacre plus de temps au sport afin d'atteindre l'objectif ( 1 h par jour). quelle est la durée totale de pratique physique qu'il doit au minimum prévoir ? Sur les 14 premiers jours : 700 min de sport. Sur les 21 jours : 21 x60 = 1260 min au minimum  Il en manque donc 1260 -700 = 560 min. ... .... Exercice 4. 21 points. On a créé un jeu de hasard. Lorsqu'on appuie sur le drapeau, le lutin dessine trois motifs côte à côte. Chaque motif est dessiné aléatoirement : soit une croix, soit un rectangle. Le joueur gagne si les trois motifs sont identiques. Au lancement du programme, le lutin est orienté horizontalement vers la droite. 1. Représenter le motif obtenu par le bloc rectangle. 2. Voici un exemple d'affichage obtenu. Quelle est la distance d exprimée en pas ? On avance de 100-60 = 40 pas entre chaque figure. 3. Quelle est la probabilité que le premier motif soit une croix ? On dessine une croix ou un rectangle ; donc la probabilité de dessiner une croix est 0,5. 4. Dessiner 8 affichages différents que l'on pourrait obtenir. 5. Les 8 affichages ont la même probabilité d'apparaître. Quelle est la probabilité que le joueur gagne ? 2 possibilités sur 8; la probabilité est 1 /8 = 1 /4 = 0,25. 6. On souhaite qu'il y ait deux fois plus de chances d'obtenir un rectangle qu'une croix. Il faut modifier l'instruction de la ligne 5. Si nombre aléatoire entre 1 et 3 =1alors. Exercice 5 22 points. On considère le programme de calcul suivant appliqués à des nombres entiers. Choisir un nombre. Calcculer son carré. Ajouter le nombre de départ. Nombre obtenu. 1. Vérifier que si le nombre de départ est 15, alors le nombre d'arrivée st 240. 15 2+15 =225 +15 = 240. Le tableau ci-dessous donne le résultat obtenu en fonction du nombre de départ. A B 1 Nombre choisi au départ Nombre obtenu 2 0 0 3 1 2 4 2 6 5 3 12 Quelle formule a pu être saisie dans la cellule B2 avant d'^tre tirée vers le bas ? =A2*A2 +A2. 3. On note x le nombre de départ. Ecrire en fonction de x une expression du résultat. x2 +x. Partie B. On considère l'affirmation suivante : Pour obtenir le résultat du programma, il suffit de multiplier le nombre de départ par le nombre entier qui suit. 4. Vérifier que cela est vrai pour un nombre choisi égal à 9. 92+9 = 90. 9 x (9+1) = 90. 5. Démontrer que cette affirmaion est vraie quel que soit le nombre de départ. x2 +x = x(x+1). 6. Démontrer que le nombre obtenu est pair quel que soit le nombre choisi au départ. Si le nombre choisi est pair, égal à 2k ( k entier naturel), le nombre obtenu  2k x(2k+1) est pair. Si le nombre choisi est impair, égal à 2k+1 ( k entier naturel), le nombre obtenu  (2k+1)  x(2k+2) = (2k+1)x 2x(k+1) est pair.

menu