Mathématiques, DNB Métropole, Antilles 9 / 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Exercice 1 QCM. 20 points.
1. 57 x 53 / 5 2 = 57+3-2=58.
A. 513 ; B. 55 ; C. 58 vrai.
2. La fraction irréductible égale à 630 / 882 est :
A. 5 / 7 vrai ; B. 35 / 49 ; C. 315 / 441.
630 = 2 x32 x5 x7.
882=2 x 32 x 7 x7.
x = −1+4t ; y = 6−5t ; z = 8−2t avec t réel.
  3. Une expression développée de A = (x −2)(3x +7) est :
A. 3x2+13x+14 ; B. 3x2+x+5 ; C. 3x2+x-14 vrai .
A = 3x2 +7x -6x-14 =3x2+x-14.
  4. Les solutions de l’équation (2x +1)(−x +3) = 0 sont :
A. 2 et 3 ; B. -0,5 et 3 vrai ; C.-1 et -3.
2x+1 = 0 soit x = -0,5 et -x+3 = 0 soit x = 3.
  5. Une urne contient 9 boules indiscernables au toucher : • 3 boules noires, • 4 boules blanches, • 2 boules rouges. Quelle est la probabilité de ne pas tirer de boule noire ?
A. 2 /9 ; B. 1 /3 ; C. 6 /9. Vrai.
Probabilité de tirer une boule noire = 3 / 9 = 1 / 3.
Probabilité de ne pas tirer une boule noire = 1-3 / 9 = 6 /9.

  Exercice 2. 20 points.
Yanis vit en France métropolitaine. Il part cet été en Guadeloupe en vacances. Il se renseigne quant aux locations de véhicules. Une société de location de voitures à Pointe-à-Pitre propose les tarifs suivants pour un véhicule 5 places de taille moyenne, assurances non comprises :
 • Tarif « Affaire » : 0,50 € par kilomètre parcouru.
• Tarif « Voyage court » : un forfait de 120 € puis 20 centimes par kilomètre parcouru
• Tarif « Voyage long » : un forfait de 230 €, quel que soit le nombre de kilomètres effectués.
 1. Yanis a préparé son plan de route et il fera 280 km. Il choisit le tarif « Affaire ». Combien va-t-il payer ?
0,50 x280=140 €.
 2. S’il parcourt 450 km, quelle offre est la plus avantageuse financièrement ?
"Affaire" : 450 x0,50 = 225 €.
" Voyage court" : 120 +0,20 x 450=210 €.
" Voyage long" : 230 €.
3. Dans la suite, x désigne le nombre de kilomètres parcourus en voiture. On considère les trois fonctions l, m, n suivantes :
 l(x) = 230 ;  m(x) = 0,5 x ; n(x) = 0,2x +120.
 a. Associer, sans justifier, chacune de ces fonctions au tarif correspondant.
"Affaire" : m(x) = 0,5 x.
"Voyage court" : n(x) = 0,2x +120.
"Voyage long" :  l(x) = 230.
 b. Déterminer le nombre de kilomètres à parcourir pour que le tarif « Voyage court » soit égal au tarif « Affaire ».
0,2x +120=0,5x ; 120 = 0,3 x ; = 120 / 0,3 = 400.
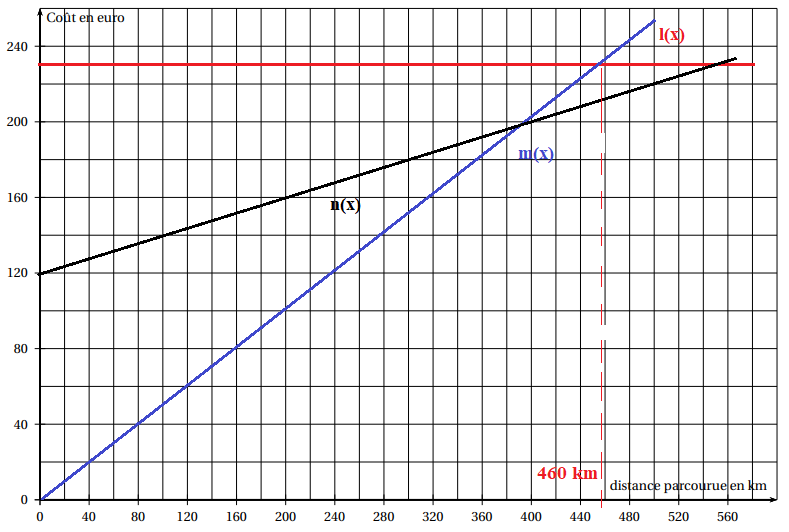
 4. a. Tracer les courbes représentatives des fonctions l, m et n
 b. Déterminez graphiquement le nombre de kilomètres que devra atteindre Yanis pour que le tarif « Voyage long »soit le plus avantageux. On laissera les traits de constructions apparents sur le graphique.

...
....

 Exercice 3. 20 points.
La figure ci-dessous est un pavage constitué de cerfs-volants. Les triangles SLP et PLA ainsi formés sont des triangles équilatéraux.

PARTIE A :
1. Déterminer la mesure de l’angle PSL ?
Dans un triangle équilatéral, les angles mesurent 60 °.
 2. Quelle est l’image du cerf-volant 2 par la symétrie d’axe (PL) ? On ne demande pas de justification.
Cerf-volant 5.
3. Déterminer par quelle transformation du plan le cerf-volant 1 devient le cerf-volant 6 ? On ne demande pas de justification.
Symétrie de  centre J.
PARTIE B : Dans cette partie, on se propose de construire le cerf-volant ci-dessous.

Essya, Nicolas et Tiago souhaitent construire cette figure à l’aide d’un logiciel de programmation. Ils écrivent tous un programme « Cerf-volant » différent.

1. Tracer le programme « Cerf-Volant » de Nicolas, en prenant 1 cm pour 100 pas.
 2. Un élève a écrit le script correct. Donner le nom de cet élève en justifiant la réponse.

 EXERCICE 4 20 points.
 Voici le nombre de passages de véhicules au péage du pont de l’île de Ré au cours de l’année 2020, reporté dans une feuille de calcul :

A
 B
1
 Mois
 Nombre de passages
2
 janvier
 210 320
3
 février
 218 464
4
 mars
 138 395
5
avril
 62 930
6
 mai
 179 699
7
 juin
 295 333
8
 juillet
 389 250
9
 août
 376 551
10
 septembre
 313 552
11
 octobre
 267 884
12
 novembre
 142 152
13
 décembre
 206 662
14
 Total
 2 801 172

1. Quelle formule a-t-on saisi dans la cellule B14 pour obtenir le nombre total de passages en 2020 ?
= Somme(B2:B13)
 2. Calculer le nombre moyen de passages par mois.
2 801 172 / 12 =233 431.
 3. Donner l’étendue de la série.
389 250 -138 395=250 885.
4. Afin d’étudier les effets du confinement de 2020, on souhaite comparer le nombre de passages de véhicules sur le pont de l’île de Ré du mois de mai 2020 avec celui du mois de mai 2021. En mai 2021, 305 214 véhicules ont passé le péage du pont. Calculer le pourcentage d’augmentation du nombre de passages de véhicules entre mai 2020 et mai 2021. Arrondir à l’unité.
(305 214-179 699)/ 179 699 ~0,7  (70 %).
 5. Sachant que le pont a une longueur de 3 000 mètres, quelle est la vitesse moyenne, exprimée en km/h, d’un cycliste qui le traverse en 10 minutes ?
3000 m = 3 km ; 10 min = 1 / 6 heure.
Vitesse = 3 / (1/6) = 18 km / h.

EXERCICE 5 20 points.
 Lya passe la journée dans un parc aquatique. Elle y trouve une cabane dans un chêne d’où part une tyrolienne qui mène au-dessus d’une piscine. Le câble de la tyrolienne relie la cabane et le pied du peuplier situé juste derrière la piscine.

La réglementation exige que l’angle formé par le câble de la tyrolienne et l’horizontale ait une mesure inférieure à 30°.
 La piscine a la forme d’un parallélépipède rectangle de longueur 6 m, largeur 6 m et profondeur 1,60 m.
Lorsque Lya est suspendue à la tyrolienne, corps et bras tendus, elle mesure exactement 1,50 m.
1. Vérifier par un calcul que BC = 20 m.
BC = 12,20 + longueur piscine +1,80 = 12,20 + 6 +1,80 =20 m.
2. Le positionnement de la tyrolienne est-il conforme à la réglementation en vigueur ?
tan ( angle BCA) = 5,50 / 20 =0,275 ; angle BCA ~15° < 30°.
3. Déterminer la longueur AC, en mètres, de câble nécessaire. Arrondir à l’unité.
Relation de Pythagore dans le triangle ABC rectangle en B.
AC2 = AB2 +BC2 =5,52 + 202 =430,25 ; AC ~21 m.
 4. Lya est suspendue à la tyrolienne verticalement. À quelle distance DC du peuplier, en mètres, les pieds de Lya toucheront-ils l’eau de la piscine ? Arrondir au centième.
Relation de Thalès : AB / DE = BC / CD ; CD = BC x DE / AB =20 x1,5 / 5,5 =5,46 m.
5. Calculer le volume de la piscine, en m3 ?
Longueur x largeur x profondeur = 6 x 6 x1,6 =57,6 m3.

  
menu