Math�matiques, brevet DNB, M�tropole 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.

.
. . .

.
.
.. ..
......


...
Exercice 1. 20 points.
Une famille se prom�ne au bord d’une rivi�re. Les enfants aimeraient conna�tre la largeur de la rivi�re. Ils prennent des rep�res, comptent leurs pas et dessinent le sch�ma ci-dessous sur lequel les points C, E et D, de m�me que A, E et B sont align�s. (Le sch�ma n’est pas � l’�chelle.)

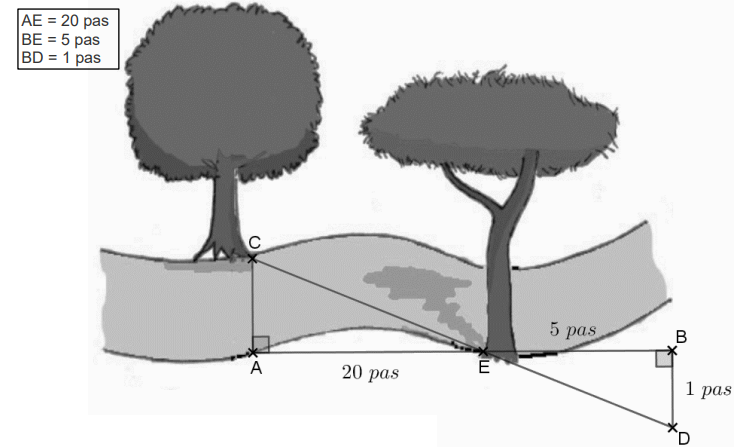1. D�montrer que les droites (AC) et (BD) sont parall�les.
Les droites (AC) et (BD) sont perpendiculaires � la droite (AB). Elles sont donc parall�les.
2. D�terminer, en nombre de pas, la largeur AC de la rivi�re.
Propri�t� de Thal�s : AC / BD = AE / BE ; AC / 1 = 20 / 5 = 4 pas.
Pour les questions qui suivent, on assimile la longueur d’un pas � 65 cm.
3. Montrer que la longueur CE vaut 13,3 m, en arrondissant au d�cim�tre pr�s.
Pythagore dans le triangle rectangle ACE :
 CE2 = AC2 + AE2 =42 +202 =416 ; CE ~20,4 pas
CE ~20,4 x0,65 ~13,3 m.
 4. L’un des enfants l�che un b�ton dans la rivi�re au niveau du point E. Avec le courant, le b�ton se d�place en ligne droite en 5 secondes jusqu’au point C.
 a. Calculer la vitesse du b�ton en m/s.
Vitesse = distance / temps = 13,3 / 5 =2,65 m /s.
b. Est-il vrai que � le b�ton se d�place � une vitesse moyenne inf�rieure � 10 km/h � ? Vrai.
2,65 x 3,6 ~ 9,5 km / h.

  Exercice 2 ( 20 points)
Cet exercice est un questionnaire � choix multiples (QCM). Aucune justification n’est demand�e. Pour chaque question, trois r�ponses (A, B et C) sont propos�es. Une seule r�ponse est exacte.

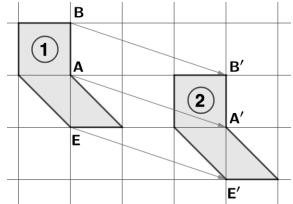
1. On consid�re les deux figures suivantes. Par quelle transformation la figure 2 est-elle l’image de la figure 1 ?
Translation, homoth�sie; sym�trie axiale.


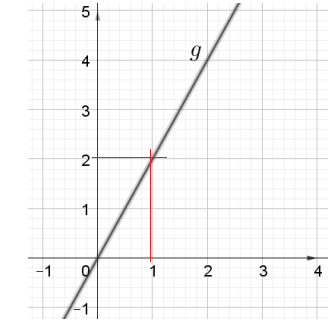
2.  On consid�re la repr�sentation graphique de la fonction g suivante : Quel est l’ant�c�dent de 2 par la fonction g ?
g(1)=2.

 3. Soit f la fonction d�finie par : f(x)=3𝑥 2 − 7 Quelle affirmation est correcte ?
29 est l'image de 2 par la fonction f. Faux.
f(2) = 3 *22-7 =5.
f(3)=20. Vrai.
f(3) = 3 *32 -7 =20.
f est une fonction affine. Faux.
 4. On a relev� les performances, en m�tres, obtenues au lancer du poids par un groupe de 13 �l�ves d’une classe.
 3,41 m ; 5,25 m ; 5,42 m ; 4,3 m ; 6,11 m ; 4,28 m ; 5,15 m ; 3,7 m ; 6,07 m ; 5,82 m ; 4,62 m ; 4,91 m ; 4,01 m.
 Quelle est la m�diane de cette s�rie de valeurs ?
7 ; 4,91 ; 5,15.
Ordonner la s�rie :
3,41 ; 3,7 ; 4,01 ; 4,28 ; 4,3 ; 4,62 ; 4,91 ; 5,15 ; 5,25 ; 5,42 ; 5,82 ;  6,07 ; 6,11.
La m�diane est la 7�me valeur soit : 4,91 m.
5. On consid�re la configuration suivante, dans laquelle les triangles LAC et BUT sont semblables. Par quel nombre doit-on multiplier l’aire du triangle LAC pour obtenir l’aire du triangle BUT ?
3 ; 6 ; 9.

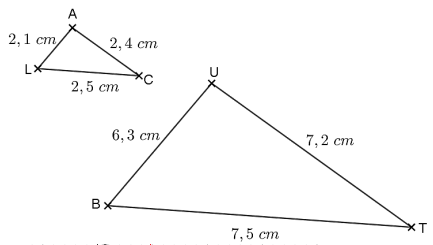
Chaque c�t� est multipli� par 3 ; l'aire est multipli�e par 9.

Exercice 3. 20 points.
Une collectionneuse compte ses cartes Pok�mon afin de les revendre. Elle poss�de 252 cartes de type � feu � et 156 cartes de type � terre �.
1. a. Parmi les trois propositions suivantes, laquelle correspond � la d�composition en produit de facteurs premiers du nombre 252 :
 Proposition 1 : 2 2 � 9 � 7. Faux, 9 n'est pas premier.
 Proposition 2  : 2 � 2 � 3 � 21. Faux, 21 n'est pas premier.
 Proposition 3:  2 2 � 32 � 7. Vrai.
 b. Donner la d�composition en produit de facteurs premiers du nombre 156.
156 = 22 x3 x13.
2. Elle veut r�aliser des paquets identiques, c’est � dire contenant chacun le m�me nombre de cartes � terre � et le m�me nombre de cartes � feu � en utilisant toutes ses cartes.
 a. Peut-elle faire 36 paquets ? Non.
PGDC(156 ; 252 ) =22 x3 = 12.
 b. Quel est le nombre maximum de paquets qu’elle peut r�aliser ?
Elle peut r�aliser au maximum 12 paquets.
 c. Combien de cartes de chaque type contient alors chaque paquet ?
252 / 12 = 21 cartes de type "feu".
156 / 12 = 13 cartes de type "terre".
3. Elle choisit une carte au hasard parmi toutes ses cartes. On suppose les cartes indiscernables au toucher. Calculer la probabilit� que ce soit une carte de type � terre �.
Nombre total de cartes : 252 + 156 = 408.
Probabilit�  de tirer une carte de type "terre" : 156 / 408 =13 / 34~0,38.

...
....

 Exercice 4. 20 points.
Dans cet exercice, 𝑥 est un nombre strictement sup�rieur � 3. On s'int�resse aux deux figures g�om�triques dessin�es ci-dessous :
 un rectangle dont les c�t�s ont pour longueurs 𝑥 − 3 et 𝑥 + 7 ;
 un carr� de c�t� 𝑥.
1. Quatre propositions sont �crites ci-dessous. Recopier sur la copie celle qui correspond � l'aire du carr�. On ne demande pas de justifier.
 4𝑥  ; 4 + 𝑥 ;  𝑥 2 vrai ; 2𝑥.
 2. Montrer que l'aire du rectangle est �gale � : 𝑥 2 + 4𝑥 − 21.
Aire = largeur fois longueur = (x-3)(x+7) = x2 -3x+7x-21 = 𝑥 2 + 4𝑥 − 21.
3. On a �crit le script ci-dessous dans Scratch. On veut que ce programme renvoie l’aire du rectangle lorsque l’utilisateur a rentr� une valeur de 𝑥 (strictement sup�rieure � 3). �crire sur la copie les contenus des trois cases vides des lignes 5, 6 et 7, en pr�cisant les num�ros de lignes qui correspondent � vos r�ponses.


4. On a press� la touche espace puis saisi le nombre 8. Que renvoie le programme ?
82 +4*8-21 = 75.
5. Quel nombre 𝑥 doit-on choisir pour que l'aire du rectangle soit �gale � l'aire du carr� ?
𝑥 2 + 4𝑥 − 21 = x2 soit 4x-21 = 0 ; x = 21 / 4.

Exercice 5. 20 points.
Dans une habitation, la consommation d’eau peut �tre anormalement �lev�e lorsqu’il y a une fuite d’eau. On consid�re la situation suivante :
 Une salle de bain est �quip�e d’une vasque de forme cylindrique, comme l’illustre l’image ci-dessous.
 Le robinet fuit � raison d’une goutte par seconde.
En moyenne, 20 gouttes d’eau correspondent � un millilitre (1 mL).

1. En raison de la fuite, montrer qu’il tombe 86 400 gouttes dans la vasque en une journ�e compl�te.
3600 gouttes par heure soit 24 x 3600 =86 400 gouttes par jour.
2. Calculer, en litres, le volume d’eau qui tombe dans la vasque en une semaine en raison de la fuite.
Par jour : 86 400 / 20 = 4 320 mL = 4,32 L.
En une semaine : 4,32 x 7 =30,24 litres.
3. Montrer que la vasque a un volume de 18,85 litres, arrondi au centilitre pr�s.
Rayon du cylindre : R = 2 dm.
Volume ; p R2 h = 3,14 x22 x1,5 =18,85 dm3 = 18,85 litres.
4. L’�vacuation de la vasque est ferm�e et le logement inoccup� pendant une semaine. L’eau va-t-elle d�border de la vasque ? Justifier la r�ponse.
30,24 > 18,85, l'eau va d�border.
 5. � la fin du XIXe si�cle, la consommation domestique d’eau par habitant en France �tait d’environ 17 litres par jour. Elle a fortement augment� avec la g�n�ralisation de la distribution d’eau par le robinet dans les domiciles : elle est pass�e � 165 litres par jour et par habitant en 2004. En 2018, la consommation des Fran�ais baisse l�g�rement pour atteindre 148 litres d'eau par jour et par habitant. Calculer le pourcentage de diminution de la consommation quotidienne d’eau par habitant entre 2004 et 2018. On arrondira ce pourcentage � l’unit�.
(165-148) / 165 ~0,10 soit10 %.

  
menu