Mathématiques, brevet DNB, Centres étrangers 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Exercice 1. 19 points.
Partie A. QCM
On considère la fonction définie par f(x) = 2x+3.
  1. La représentation graphique de cette fonction est :

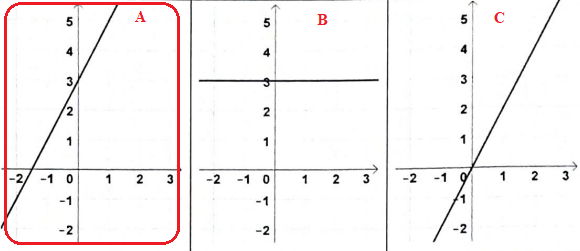 2. L'image de -2 par la fonction f est : -7 ; -1 ; 3.
f(-2) = 2 *(-2) +3= -1
3. Dans la feuille de calcul suivante, la formule à saisir en B2 avant de l'étirer vers la droite est :
= 2*A1+3 ; =2*B1+3 ; =2*(-2)+3.


Partie B.
1. Montrer que  :(2x-1)(3x+4) -2x = 6x2+3x-4.
On développe : (2x-1)(3x+4) -2x =6x2+8x-3x+4-2x =6x2+3x-4.
.
  2. On considère le triangle CDE tel que : CD = 3,6 cm ; CE = 4,2 cm ; DE = 5,5 cm. Ce triangle est'il rectangle ?
CD2 = 3,62 =12,96.
CE2 = 4,22 =17,64.
DE2 = 5,52 =30,25.
CD2 +CE2 =30,6 différent de DE2.
Ce triangle n'est pas rectangle.

  Exercice 2 ( 20 points)
La course cyliste Paris-Nice se déroule en 7 étapes. On étudie la série des distances ( en km) parcourues par étape :
93  (accidenté); 119,5 ; 166 (accidenté) ; 187,5 (accidenté) ; 188 ; 200 ; 202,5 (accidenté).
1.a Calculer la distance moyenne.
(93 +119,5 +166 +187,5 +188 +200 +202,5) / 7 =165,2 km.
b. Calculer la médiane des distances parcourues par étape.
187,5 km.
c. Calculer l'étendue de cette série.
202,5-93=109,5 km.
2. Un journaliste affirme " environ 57 % du nombre total d'étapes se sont déroulés sur un parcours accidenté. A-t-il raison ?
A étapes accidentées sur 7 soit 4 / 7 ~0,571 ( 57 ,1 %). Il a raison..

3. Le premier a remporté la course en 28 h 50 min. Le dernier a mis 30 h 12 min.
Quel est le retard du dernier par rapport au vainqueur ?
30 h 12 = 30x60 +12 =1812 min.
28 h 50 = 28*60 +50 =1730 min.
1812-1730=82 min ou 1 h 22 min.
  4. Le vainqueur a remporté la premièee étape (166 km ) en 3 h 51 min. Déterminer sa vitesse moyenne en km / h arrondie à l'unité.
3 x60 +51 = 231 minutes.
166 / 231 x 60 =43,1 ~43 km / h.

Exercice 3. 21 points.
On considère la figure suivante, où toutes les longueurs sont en cm.


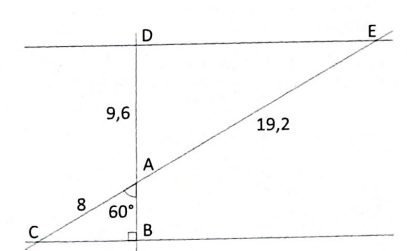1. Prouver que [AB] = 4 cm.
Dans le triangle rectangle ABC : cos 60 = AB / AC  ; AB = AC cos 60 = 8 x cos 60 =4 cm.
2. Démontrer que les droites (BC) et (DE) sont parallèles.
AD / AB = 9,6 / 4 =2,4 ;
AE / AC = 19,2 / 8 =2,4.
AD / AB =AE / AC.
D'après la réciproque du theorème de Thalès, les droites (BC) et (DE) sont parallèles.
3. En déduire que la droite (DB) est perpendiculaire à la droite (DE).
(DB) est perpendiculaire à (BC).
(BC) et (DE) sont parallèles.
Donc (DB) est perpendiculaire à la droite (DE).
4. Calculer l'aire du triangle ADE.
DE2 = AE2-AD2 = 19,22 -9,62= 276,46 ; DE ~16,63 cm.
Aire du triangle ADE :
DE x DA / 2 = 9,6 x16,63 / 2 ~80 cm2.

...
....

 Exercice 4. 15 points.
Toutes les longueurs sont exprimées en pixel.
Un professeur donne à ses élèves un motif en forme de parallèlogramme et le script, en partie rédigé, qui permet de tracer ce motiff. Le lutin est au point de départ comme indiqué sur la figure et orienté vers la droite.
Recopier dans le bon ordre les instructions suivantes à insérer dans le script du motif permettant de tracer le parallèloghramme.

Partie B.
Le professeur demande à ses élèves d'intégrer ce sript dans un programme de leur choix permettant de tracer des figures composées de plusieurs de ces motifs.
Voici les programmes écrits par deux élèves.
Programme A
 Programme B
Quand flèche droite est pressée
Effacer tout
aller à x = 230 y = 150
s'orienter à 90°
Répéter 9 fois
style en position écriture
Motif
relever le style
avancer de 50
 Quand espace est pressé
effacer tout
aller à x=0 y=0
style en position écriture
répéter 9 fois
motif
Tourner de 40° sens antihoraire
relever le style
1. Quelle action du clavier permet de lancer le programme B ?
Appuyer sur la barre d'espace.
2. Indiquer la figure obtenue par A et par B.


Exercice 5. 25 points.
Pour féter les 25 ans de sa boutique, un chocolatier souhaite offrir aux premiers clients de la journée une boîte contenant des trufes au chocolat.
1. Il a confectionner 300 truffes : 125 parfumées au café et 175enrobées de noix de coco.
Il souhaite fabriquer ces boîtes de sorte que :
- le nombre de truffes parfumées au chocolat soit le même dans chaque boîte
- le nombre de truffes enrobées de noix de coco soit le même dans chaque boîte
- totes les truffes seront utilisées.
a. Décomposer 125 et 175  en produit de facteurs premiers.
125 = 53.
175 = 52 x 7.
b. En déduire la liste des diviseurs communs à 125 et 175.
1 ; 5 ; 25.
c. Quel nombre maximal de boîtes pourrat-on réaliser ?
25 boîtes.
d. Combien y aura-t-il de truffes dans chaque boîte ?
5 truffes parfumées au chocolat et 7 truffes enrobées de noix de coco.
2. Le chocoaltier souhaite fabriquer des boîtes contenant 12 truffes. Il a le choix entre deux types de boîtes.

Chaque truffe est assimilée à une boule de diamètre 1,5 cm.
A l'intérieur des boîtes, pour que les truffes ne s'abiment pas durant le transport, le volume occupé par les truffes doit être supérieur au volume non occupé par les truffes.
Quel type de boîte faut-il choisir pour que cette condition soit respectée ?
Volume d'une truffe : 4 / 3 p r3 =4 / 3 x3,14 x0,753 = 1,77 cm3.
Volume des 12 truffes : 21,2 cm3.
Volume du pavé droit : 5 x3,5 x3,5 =61,25 cm3.
Volume non occupé par les truffes : 61,25 -21,2 ~40 cm3.
Cette boîte ne convient pas.
Volume de la pyramide : aire de base x hauteur / 3 =4,8 x4,8 x5 / 3=38,4 cm3.
Volume non occupé par les truffes : 38,4 -21,2 ~17,2 cm3.
Cette boîte convient.

  
menu